CHƯƠNG 7: PHƯƠNG TRÌNH VẬT LÝ - TOÁN
§1. PHÂN LOẠI CÁC PHƯƠNG TRÌNH ĐẠO HÀM RIÊNG TUYẾN TÍNH
CẤP 2 VỚI CÁC BIẾN ĐỘC LẬP
1. Phân loại các phương trình: Khi khảo sát các bài toán vật lí, ta nhận được phương
trình đạo hàm riêng cấp 2 dạng:
)x(du)x(c
x
u
)x(b
yx
u
)x(a n
1i i
i
n
1j,i ji
2
j,i =+
∂
∂
+
∂∂
∂∑∑ ==
(1)
Trong đó aij(x), bi(x), c(x) và d(x) là các hàm nhiều biến đã cho của x = (x1, x2,...xn)
còn u(x) là các hàm cần xác định.
Trong thực tế ta thường gặp các phương trình đạo hàm riêng tuyến tính cấp 2
với hai biến độc lập dạng:
hgu
y
u
e
x
u
d
y
u
c
yx
u
b2
x
u
a2
22
2
2
=+
∂
∂
+
∂
∂
+
∂
∂
+
∂∂
∂
+
∂
∂ (2)
Trong đó a, b, c, d, g, h là các hàm hai biến của x và y.
Trong giáo trình này ta chỉ xét các phương trình dạng (2). Để đơn giản ta viết lại (2):
0
y
u
,
x
u
,u,y,x
y
u
c
yx
u
b2
x
u
a2
22
2
2
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
Φ+
∂
∂
+
∂∂
∂
+
∂
∂ (3)
Các phương trình này có thể phân thành các loại sau:
Phương trình hyperbolic:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
Φ=
∂∂
∂
y
u
,
x
u
,u,y,x
yx
u
1
2
Phương trình eliptic:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
Φ=
∂
∂
+
∂
∂
y
u
,
x
u
,u,y,x
y
u
x
u
2
2
2
2
2
Phương trình parabolic:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
Φ=
∂
∂
y
u
,
x
u
,u,y,x
x
u
3
2
2
2. Các bài toán cơ bản của phương trình vật lí - toán:
a. Bài toán Cauchy và bài toán hỗn hợp của phương trình truyền sóng: Một
phương trình truyền sóng là một phương trình dạng hyperbolic. Phương trình truyền
sóng dạng chính tắc là:
()
t,z,y,xf
z
u
y
u
x
u
a
t
)t,z,y,x(u
1
2
2
2
2
2
2
2
2
2
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
Giả sử ta cần xác định hàm u(x, y, z, t) trong miền V và t ≥ 0. V được giới hạn bằng
mặt biên kín và trơn S với các điều kiện đầu:
)z,y,x(u)t,z,y,x(u o
0t =
=
)z,y,x(u
t
u
o
0t
∗
=
=
∂
∂
150
và điều kiện biên:
)z,y,x(u)t,z,y,x(u 1
S)z,y,x( =
∈
Bài toán giải phương trình trên với các điều kiện đầu và điều kiện biên được gọi là bài
toán hỗn hợp của phương trình truyền sóng. Nếu ta xét bài toán trong miền cách xa
các biên mà ở đó điều kiện biên không có tác dụng thì ta gặp bài toán Cauchy với điều
kiện đầu và xét trong toàn bộ không gian.
b. Bài toán Cauchy và bài toán hỗn hợp của phương trình truyền nhiệt: Cho
phương trình truyền nhiệt dưới dạng chính tắc:
()
t,z,y,xf
z
u
y
u
x
u
a
t
)t,z,y,x(u
1
2
2
2
2
2
2
2+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
Khi đó bài toán hỗn hợp của phương trình truyền nhiệt là bài toán tìm nghiệm của
phương trình với điều kiện đầu và điều kiện biên:
)z,y,x(u)t,z,y,x(u o
0t =
=
)z,y,x(u)t,z,y,x(u 1
S)z,y,x( =
∈
Bài toán Cauchy của phương trình truyền nhiệt là bài toán tìm nghiệm của phương
trình truyền nhiệt trong toàn bộ không gian.
§2. PHƯƠNG TRÌNH LOẠI HYPERBOLIC
PHƯƠNG TRÌNH TRUYỀN NHIỆT
1. Bài toán Cauchy - Phương trình sóng của dây vô hạn và nửa vô hạn: Bài toán
Cauchy của phương trình hyperbolic trong trường hợp một biến được xác định như
sau:
2
2
2
2
2
x
u
a
t
)t,x(u
∂
∂
=
∂
∂ -∞ ≤ x ≤ ∞, t ≥ 0 (1)
với các điều kiện
)x(u)t,x(u o
0t =
=; )x(u
t
u
1
0t
=
∂
∂
=
(2)
Đây là bài toán dao động tự do của dây dài vô hạn.
Để giải phương trình (1) ta biến đổi nó bằng cách dùng các biến:
atxη
a
t
xξ
−=
+= (3)
nghĩa là:
2
ηξ
x+
= a2
ηξ
t−
=
Ta có:
η
u
~
ξ
u
~
x
u
~
∂
∂
+
∂
∂
=
∂
∂
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
−
∂
∂
=
∂
∂
η
u
~
ξ
u
~
a
t
u
~
2
22
2
2
2
2
η
u
~
ηξ
u
~
2
ξ
u
~
x
u
~
∂
∂
+
∂∂
∂
+
∂
∂
=
∂
∂
151
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
∂∂
∂
−
∂
∂
=
∂
∂
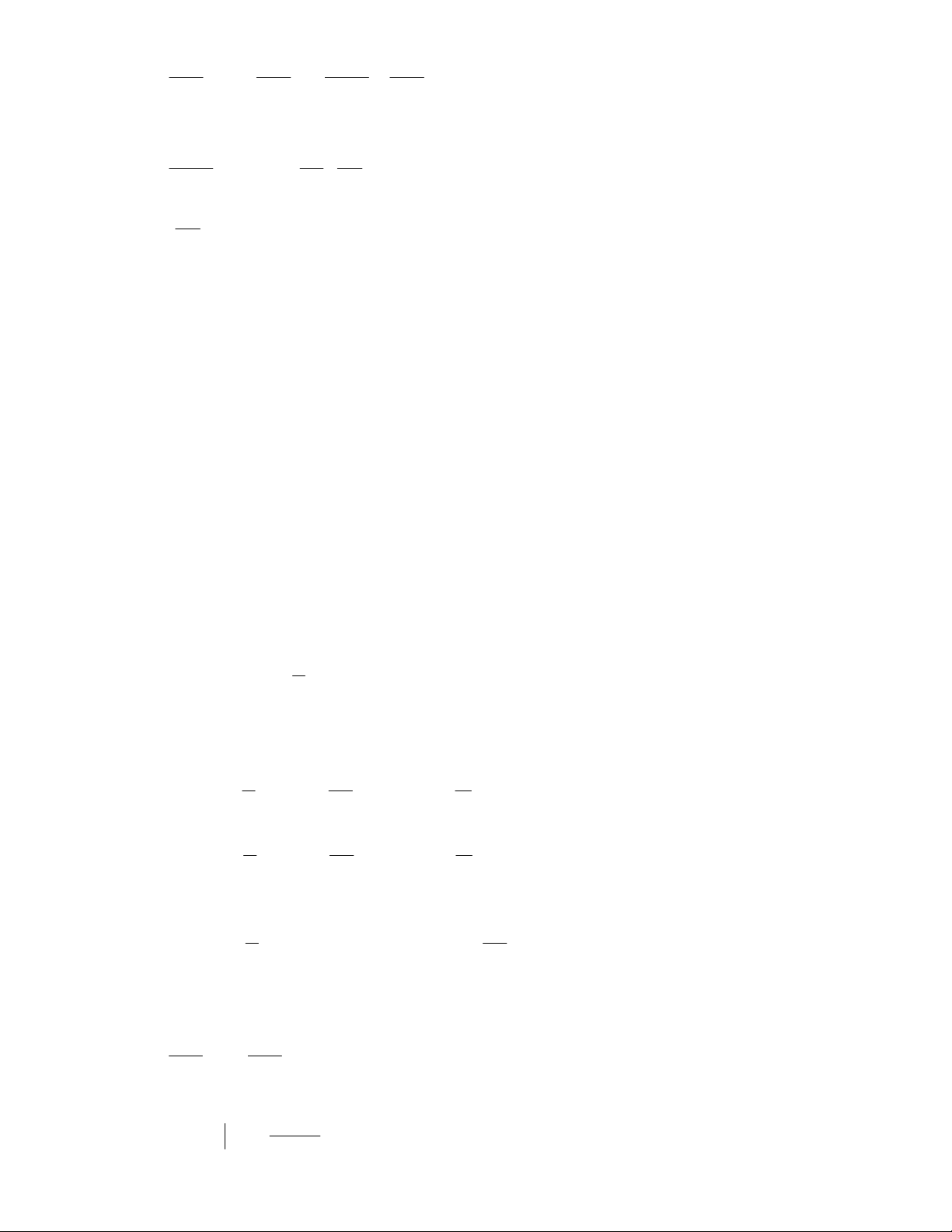
2
22
2
2
2
2
2
η
u
~
ηξ
u
~
2
ξ
u
~
a
t
u
~
Thay vào (2.1) ta có:
0
ξ
u
~
η
hay0
ηξ
u
~
2
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
=
∂∂
∂
Suy ra: =
∂
∂
ξ
u
~
ϕ1(ξ) với ϕ1(ξ) là hàm tuỳ ý
Như vậy:
∫+= )η(ψξd)ξ(φ)η,ξ(u
~
1
với ψ(η) là hàm tuỳ ý.
Từ đó ta có:
)η,ξ(u
~
= ϕ(ξ) + ψ(η)
hay: u(x, t) = ϕ(x + at) + ψ(x - at) (3)
Trong đó ϕ và ψ là các hàm tuỳ ý, liên tục và khả vi 2 lần. Nghiệm của (3) được gọi
là nghiệm tổng của (1). Từ (3) nếu tính đến điều kiện (2) ta sẽ có:
ϕ(x) + ψ(x) = uo(x) (4)
aϕ(x) - aψ(x) = u1(x) (5)
Lấy tích phân hai vế của (5) ta có:
[][]
∫
=−−− x
0
1θd)θ(u)0(ψ)x(ψa)0(φ)x(φa
Vậy nên:
Cθd)θ(u
a
1
)x(ψ)x(φ
x
0
1+=− ∫ (6)
với C = ϕ(0) - ψ(0)
Từ (4) và (6) rút ra:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−−=
++=
∫
∫
2
C
θd)θ(u
a2
1
)x(u
2
1
)x(ψ
2
C
θd)θ(u
a2
1
)x(u
2
1
)x(φ
x
0
1o
x
0
1o
Đặt các hệ thức trên vào (3) ta được nghiệm:
[]
∫
+
−
+−++= atx
atx
1oo θd)θ(u
a2
1
)atx(u)atx(u
2
1
)t,x(u
Đây là công thức D’Alembert.
Ví dụ 1: Giải phương trình:
2
2
2
2
2
x
u
a
t
u
∂
∂
=
∂
∂ -∞ < x < ∞, t ≥ 0
với các điều kiện:
)x(u
x1
x
)t,x(u o
2
0t =
+
=
=
152
)x(uxsin
t
u
1
0t
==
∂
∂
=
Áp dụng công thức D’Alembert ta có:
xsinatsin
a
1
)atx(1
atx
)atx(1
atx
2
1
)t,x(u 22 +
⎥
⎦
⎤
⎢
⎣
⎡
−+
+
+
++
+
=
Ví dụ 2: Giải phương trình:
2
2
2
2
2
x
u
a
t
u
∂
∂
=
∂
∂ -∞ < x < ∞, t ≥ 0
với các điều kiện:
)x(u
x1
1
t
u
)x(u
x
xsin
)t,x(u
1
2
0t
o
0t
=
+
=
∂
∂
==
=
=
Áp dụng công thức D’Alembert ta có:
⎥
⎦
⎤
⎢
⎣
⎡
−+
+
−
−
=2222 )at(x1
at2
arctg
a2
1
)at(x
atsinxcosatatcosxsinx
)t,x(u
vì nếu đặt arctg(x + at) - arctg(x - at) = α ta có:
[]
[
]
[][]
22 )at(x1
at2
)atx)(atx(1
)atx()atx(
)atx(arctgtg)atx(arctgtg1
)atx(arctgtg)atx(arctgtg
αtg
−+
=
−++
−
=
−×++
−+
=
Ví dụ 3: Giải phương trình:
2
2
2
2
2
x
u
a
t
u
∂
∂
=
∂
∂ -∞ < x < ∞, t ≥ 0
với các điều kiện:
0)t,x(u
)x(uxsin
t
u
)x(ux)t,x(u
0x
1
2
0t
o
2
0t
=
==
∂
∂
==
=
=
=
Trước hết để tìm nghiệm của bài toán ta kéo dài lẻ hàm uo(x) = x2 và u1(x) = sin2x sẽ
được các hàm:
⎩
⎨
⎧
<−
≥
=
∗
0xx
0xx
u2
2
o
⎩
⎨
⎧
<−
≥
=
∗
0xxsin
0xxsin
u2
2
1
Áp dụng công thức D’Alembert cho các hàm này ta có:
153
[]
[]
[]
[]
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−+
≤−++
=
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>>
⎥
⎦
⎤
⎢
⎣
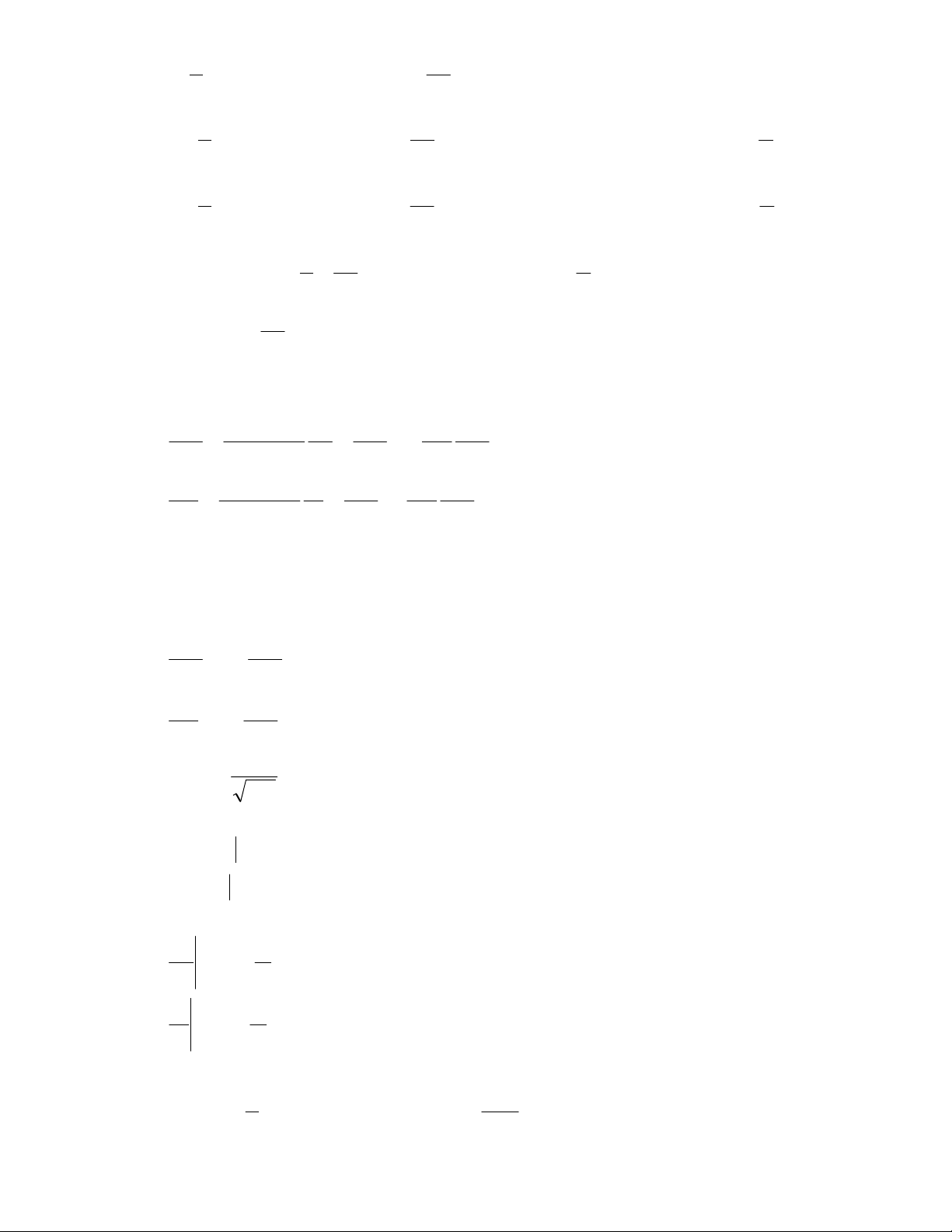
⎡θθ−θθ+−−+
≤θθ+−++
=
θθ+−++=
∫∫
∫
∫
+
−
+
−
+
−
∗∗∗
at2cosx2sinx2
a4
1
axt2
a
x
tat2sinx2cos
a4
1
2
t
tax
0
a
x
td)(sind)(sin
a2
1
)atx()atx(
2
1
a
x
td)(sin
a2
1
)atx()atx(
2
1
d)(u
a2
1
)atx(u)atx(u
2
1
)t,x(u
222
atx
0
0
atx
2222
atx
atx
222
atx
atx
1oo
Ví dụ 4: Giải phương trình điện báo:
0
x
u
LC
1
u
LC
RG
t
u
LC
LGRC
t
u
2
2
2
2
=
∂
∂
−+
∂
∂+
+
∂
∂
0
x
i
LC
1
i
LC
RG
t
i
LC
LGRC
t
i
2
2
2
2
=
∂
∂
−+
∂
∂+
+
∂
∂
Trong các trường hợp:
- Dây không tổn hao R = G = 0
- Dây không méo RC = LG
) Trường hợp dây không tổn hao: Khi đó các phương trình trên có dạng:
2
2
2
2
2
2
2
2
2
2
x
i
a
t
i
x
u
a
t
u
∂
∂
=
∂
∂
∂
∂
=
∂
∂
Trong đó LC
1
a=
Giả sử các điều kiện ban đầu đã biết là:
⎪
⎩
⎪
⎨
⎧
=
=
=
=
)x(i)t,x(i
)x(u)t,x(u
o
0t
o
0t -∞ < x < ∞, y > 0
Với R = G = 0 ta có điều kiện đối với phương trình điện báo:
)x(i
C
1
t
u
o
0t
−=
∂
∂
=
)x(u
C
1
t
i
o
0t
−=
∂
∂
=
Từ đó áp dụng các công thức D’Alembert ta được:
[]
∫
+
−
θθ−−++= atx
atx
ooo d)(i
aC2
1
)atx(u)atx(u
2
1
)t,x(u
154