7
Pr{B}= 1- µΔt
Giả thiết Pr{C}= 0, với 1/µ là thời gian phục vụ trung bình (thực tế được
phân bố theo hàm mũ.
D là sự kiện của 1 hoặc nhiều sự đến AND với sự kiện của 1 hoặc
nhiều sự đi trong khoảng Δt
Giả sử Pr{D}=0, (2-1)
Thực ra, nó chỉ ra rằng khi Δt nhỏ, sự kiện nhân (vừa đi vừa đến) là
không xảy ra.
Ngoài các giả thiết trên về đặc tính của tiến trình đến và tiến trình phục
vụ, còn có thêm các giả thiết sau:
Tiến trình đến là tiến trình Poisson với tham số λ
Khoảng thời gian đến phân bố theo hàm mũ với tham số 1/λ
Thời gian phục vụ phân bố theo hàm mũ với tham số 1/µ
Tiến trình đến là độc lập với tiến trình phục vụ và ngược lại
Để phân tích hệ thống hàng đợi cần hiểu khái niệm “Trạng thái hệ
thống”. Có thể định nghĩa thông qua biến thích hợp mô tả “ Sự phát
triển theo thời gian” của hệ thống hàng đợi. Để thuận tiện cho hệ thống
hàng đợi biến được chọn sẽ là số khách hàng trong hệ thống tại thời
điểm t.
Trạng thái hệ thống tại t = N(t)= Số lượng khách hàng tại thời
điểm t (2-2)
Tức là :
pN(t)=Pr{N(t)=N} (2-3)
với
pN(t) là ký hiệu của trạng thái thứ N của hệ thống tại thời điểm t.
Pr{N(t)=N} là xác suất có N khách hàng trong hệ thống tại thời
điểm t.
Có nghĩa là có N khách hàng trong hệ thống tại thời điểm t.
Sử dụng trạng thái đầu tiên tại t=0, nếu ta có thể tìm pN(t) thì có thể
mô tả hệ thống có quan hệ về mặt thời gian như thế nào?
Tiếp theo, cho thời gian Δt →0.
Xét các trạng thái có thể của hệ thống {0,1,…}(bằng đúng số lượng
khách hàng trong hệ thống) tại thời điểm t ta có thể tìm trạng thái của
hệ thống tại thời điểm t+Δt như sau:
p0(t+Δt )= p0(t)(1-λΔt)+p1(t)µΔt, N=0.
Giáo trình hình thành công cụ phân tích
hàm mũ với tham số theo tiến trình
Poisson với tham số
8
pN(t+Δt )= pN(t)(1-λ Δt-µΔt)+pN-1(t)λΔt+ pN+1(t)µΔt,
N>0 (2-4)
ta luôn có điều kiện phân bố chuẩn:
0,1)(
ttp
i
i (2-5)
Tức là chuẩn hóa các pi(t), t≥0, thành các tính chất phân bố rời rạc
theo thời gian.
Ta có thể tính giới hạn khi Δt →0 và có hệ phương trình vi phân:
0),()()()(
)(
0),()(
)(
11
10
0
Ntptptp
dt
tdp
Ntptp
dt
tdp
NNN
N
(2-6)
Để giải ta phảo cho điều kiện ban đầu.
Giả sử rằng hệ thống hàng đợi bắt đầu tại thời điểm t=0 với N khách
hàng ở trong hệ thống, điều kiện ban đầu được viết như sau:
pi(0)=0, với i≠N
pN(0)=1, với i=N (2-7)
Sử dụng điều kiện ban đầu phù hợp hệ thống có thể được giải để
được giải pháp thời gian ngắn (transient solution), một giải pháp phức
tạp thậm chí cho các hệ đơn giản nhất.
Bây giờ ta xét giải pháp trạng thái ổn định (equilibrium solution), t→∞.
Khi đó ta có:
0,0
)(
0,0
)(
0
N
dt
tdp
N
dt
tdp
N
(2-8)
Vì vậy,
p0(t)=p0, với N=0
pN(t)=pN, với N>0 (2-9)
Định nghĩa ρ=λ /µ với ngụ ý rằng hệ thống hàng đợi ổn định với ρ <1,
ta có:
p1=ρp0
pN+1(t)=(1+ρ)pN- ρpN-1=ρpN=ρN+1p0, N>0 (2-10)
Gỉa sử tuân theo điều kiện phân bố chuẩn, ta có:
pi = ρi (1-ρ ), i=0,1,… (2-11)
với giải pháp trạng thái ổn định cho phân bố trạng thái với ρ <1.
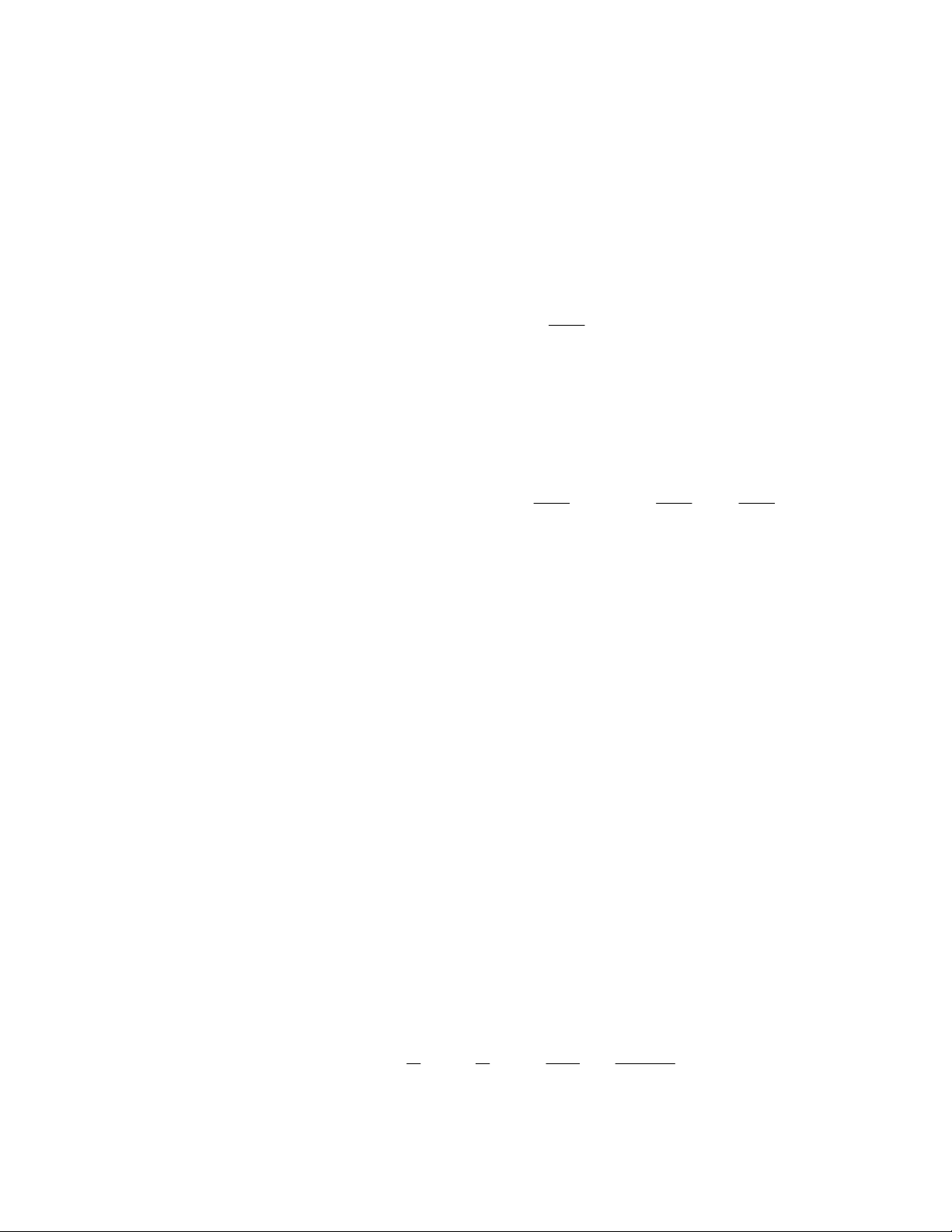
9
giải pháp trạng thái ổn định không phụ thuộc điều kiện phân bố ban
đầu. Tuy nhiên, nó cần điều kiện rằng tốc độ đến nhỏ hơn tốc độ phục
vụ.
Các tham số hiệu năng trung bình
Số lượng trung bình của khách hàng trong hệ thống
Nhắc lại rằng phân bố của trạng thái ổn định cho số lượng khách hàng
trong hệ thống khi t→∞. Ví vậy, có thể suy ra số khách hàng trung bình
trong hệ thống từ phân bố trạng thái ổn định của hệ thống như sau:
1
)1(][
00 i
i
i
iiipNE (2-12)
Kết quả trên không áp dụng cho số trung bình khách hàng trong hệ
thống tại một khoảng thời gian ngắn t (arbitrary time t).
Số lượng trung bình của khách hàng trong hàng đợi
Chú ý rằng số lượng khách hàng trong hàng đợi thì bằng với số lượng
khách hàng trong hệ thống trừ đi 1. Sử dụng cùng các giả thiết ta có:
11
)1(
1
)1(][
2
0
111
ppippiNE
i
i
i
i
i
iQ
(2-13)
Chú ý rằng tổng bắt đầu từ i=1, do sự kiện khách hàng đợi chỉ đúng
khi có nhiều hơn 0 khách hàng trong hệ thống.
Chú ý rằng (i-1)!, do đang tìm số lượng khách hàng trung bình trong
hàng đợi.
Thời gian trung bình t rong hệ thống
Thời gian này có thể được phân chia thành hai thành phần :
Thời gian đợi
Thời gian phục vụ
Tính toán các tham số hiệu năng này đòi hỏi những giả thiết thêm dựa
trên đặc tính của hệ thống hàng đợi :
Quy tắc phục vụ khách hàng : Giả sử quy tắc “ first-come, first
served” là khách hàng được phục vụ theo thứ tự như khi đến hệ
thống
Phân bố trạng thái ổn định pk, k=0,1,…, cũng giống như phân bố
xác suất của số lượng khách hàng trong hệ thống.
Thời gian phục vụ dư trung bình của khách hàng sẽ dùng để phục
vụ khi tiến trình đến xảy ra với tốc độ 1/µ, cũng giống như vậy. Vì
vậy được gọi là đặc tính không nhớ.
Sử dụng các giả thiết cho thời gian trung bình trong hệ thống của
khách hàng :
)1(
111
000
k
k
k
k
k
k
p
k
pp
k
WE (2-14)
Thời gian trung bình trong hàng đợi (thời gian đợi để được phục vụ)
10
Với các giả thiết trên ta có:
)1(
0
k
k
Qp
k
WE (2-15)
Chú ý rằng thời gian trung bình trong hàng đợi bằng với thời gian trung
bình hệ thống trừ đi thời gian phục vụ:
)1(
1
)1(
11
WEWE Q (2-16)
Có thể có khả năng rằng khách hàng phải chờ để được phục vụ
Sử dụng phân bố trạng thái ổn định pk, k=0,1,…ta chú ý rằng lượng
khách hàng đến luôn phải đợi để được phục vụ nếu số lượng khách
hàng lớn hơn 0 trong hệ thống.
Vì vậy,
Pwait=1-p0=ρ (2-17)
Sử dụng server
Ý nghĩa vật lý của tham số hiệu năng là nó đưa ra khoảng thời gian khi
server bận. vì vậy,
Pbusy=1-p0=ρ (2-18)
Các cách tiếp cận đã trình bày được sử dụng để phân tích bất kỳ một
hệ thống hàng đợi đều phải có các giả thiết sau:
Tiến trình đến là tiến trình poisson, có nghĩa là khoảng thời gian
đến được phân bố theo hàm mũ.
Tiến trình đến với tốc độ đến thay đổi.
Hệ thống có một hoặc nhiều server
Thời gian phục vụ có dạng phân bố hàm mũ
Tiến trình đến là độc lập với các tiến trình phục vụ và ngược lại
Có vô hạn các vị trí đợi hữu hạn trong hệ thống
Tất cả các giả thiết tạo thành lớp đơn giản nhất của hệ thống hàng đợi.
2.2. Nhắc lại các khái niệm thống kê cơ bản
2.2.1. Tiến trình điểm
Các tiến trình đến là một tiến trình điểm ngẫu nhiên, với tiến trình này
chúng ta có khả năng phân biệt hai sự kiện với nhau. Các thông tin về
sự đến riêng lẻ (như thời gian phục vụ, số khách hàng đến) không cần
biết, do vậy thông tin chỉ có thể dùng để quyết định xem một sự đến có
thuộc quá trình hay không.
11
Mô tả tiến trình
Chúng ta xem xét qui luật của tiến trình điểm thông thường, nghĩa là
loại trừ các tình huống đến kép. Xét số lần cuộc gọi đến với cuộc gọi
thứ i tại thời điểm Ti :
0 = T0 < T1 < T2 < < ……..< Ti < Ti+1< …… (2-19)
Lần quan sát thứ nhất tại T0 = 0.
Số các cuộc gọi trong nửa khoảng thời gian mở [0, t] là Nt, ở đây Nt là
một biến ngẫu nhiên với các tham số thời gian liên tục và thời gian rời
rạc, khi t tăng thì Nt không bao giờ giảm.
Khoảng thời gian giữa hai lần đến là:
Xi = Ti - Ti-1 (2-20)
Khoảng thời gian này gọi là khoảng thời gian giữa hai lần đến. Sự
phân bố của tiến trình này gọi là sự phân bố khoảng đến.
Tương ứng với hai biến ngẫu nhiên Nt và Xi, hai tiến trình này có thể
được mô tả theo hai cách:
Cách biểu diễn số Nt : khoảng thời gian t giữ không đổi, và ta xét
biến ngẫu nhiên Nt cho số cuộc gọi trong khoảng thời gian t.
Cách biểu diễn khoảng ti : số các cuộc gọi đến là hằng số (n), và ta
xét biến ngẫu nhiên ti là khoảng thời gian diễn ra n cuộc gọi.
Mối quan hệ căn bản giữa hai cách biểu diễn thể hiện đơn giản như
sau:
Nt < n khi và chỉ khi
n
i
in tXT
1
Điều này được biểu diễn bằng đẳng thức Feller - Jensen :
tTpnNp nt với n = 1, 2,….. (2-21)
Phân tích tiến trình điểm có thể dựa trên cả hai cách này, về nguyên
tắc chúng tương đương với nhau. Cách biểu diễn khoảng thời gian
tương ứng với việc phân tích chuỗi thời gian thông thường.
Cách biểu diễn số không song song với phân tích chuỗi thời gian. Số
liệu thống kê được tính toán trên mỗi đơn vị thời gian và ta có các mức
trung bình thời gian.
Đặc tính của tiến trình điểm
Phần này chúng xem xét đặc tính của nó thông qua cách biểu diễn số.
Tính dừng (tính đồng nhất thời gian)(Stationarity-time homogeneity) :
Tính chất này có thể mô tả là cho dù ở vị trí nào trên trục thời gian
cũng vậy, phân bố xác suất tiến trình điểm là độc lập với thời điểm
quan sát. Định nghĩa sau đây được sử dụng trong thực tế: