1
Phân tích m ô hình
hồi qui đa biến
Khái niệm vềphân tích hồi quy
Mô hình hồi qui hai biến
Phương pháp bình phương nhỏnhất
Các giảđịnh của m ô hình hồi qui đa
biến
Độchính xác và sai sốchuẩn của ước
lượng
Kiểm định giảthuyết m ô hình
Ví dụm ô hình hồi qui đa biến
2
Khái niệm vềphân tích hồi quy
Phân tích hồi quy đềcập đến việc
nghiên cứu sựphụthuộc của m ột biến
số, biến phụthuộc, vào m ột hay nhiều
biến sốkhác, biến độc lập, với ý định
ước lượng và/ hoặc dựđoán giá trị
trung bình (tổng thể) của biến phụ
thuộc dựa trên những giá trịđã biết
hay cốđịnh của biến độc lập.
3
Ví dụ1
Chúng ta quan tâm đến việc dựbáo chiều
cao trung bình của những người con khi
biết chiều cao của người cha.
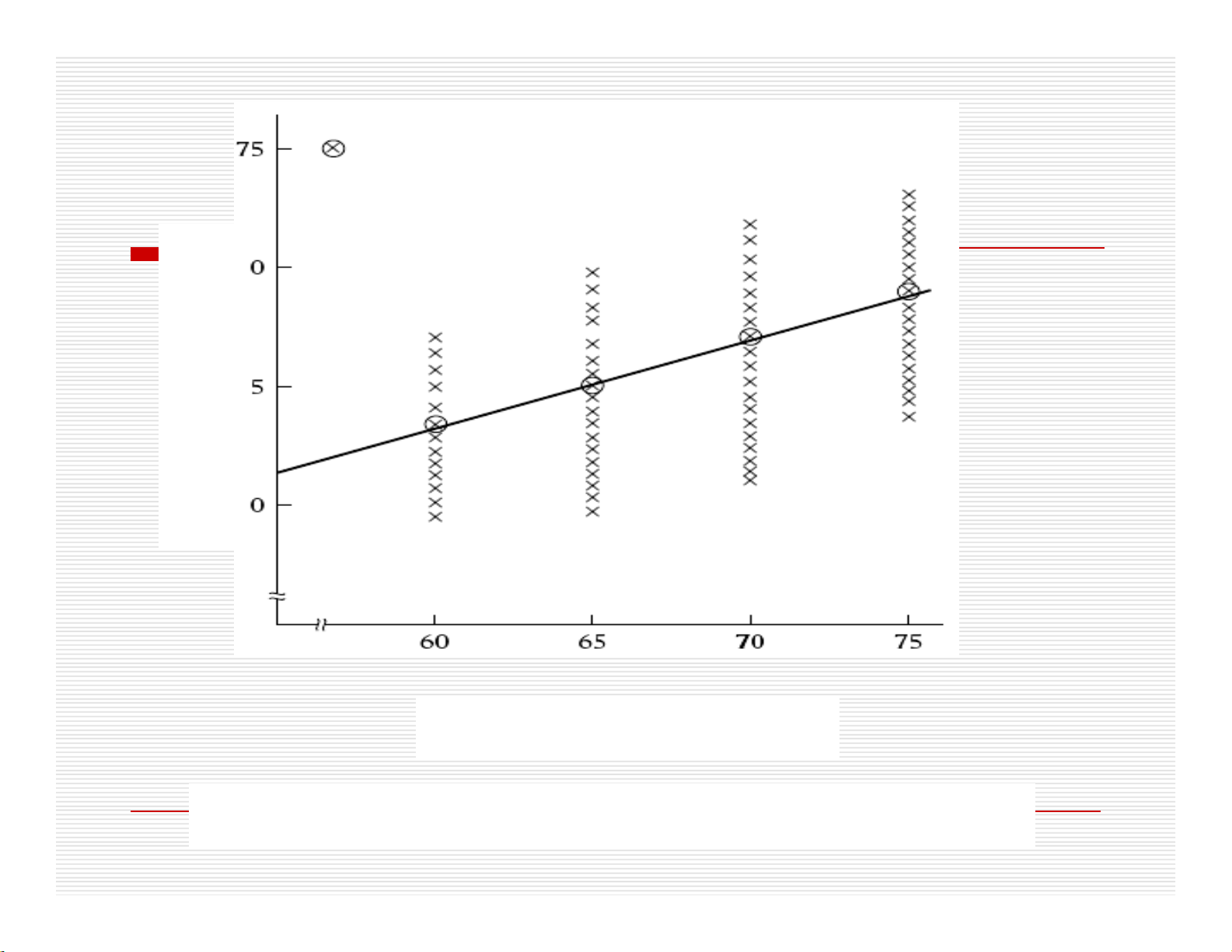
Dùng biểu đồphân tán đểbiểu diễn
phân phối chiều cao của những người con
trong m ột tổng thểtương ứng với chiều
cao của những người cha được cho trước
hay cốđịnh
4
Chiều
cao
của
người
con
(tính
bằng
inch)
Chiều cao của người cha
(tính bằng inch)
Hình 1.1 Phân phối giả thiết của chiều cao của những người con
trai tương ứng với chiều cao của người cha được cho trước
Giá trị trung bình
5
Ví dụkhác
Một nhà kinh tếcó thểquan tâm đến việc
nghiên cứu sựphụthuộc của chi tiêu cá nhân
vào thu nhập cá nhân sau thuếhay thu nhập
khảdụng thực tế.
Một nhà độc quyền, người có thể ấn định giá
hay sản lượng (nhưng không cảhai) có thể
m uốn tìm ra phản ứng của cầu đối với sản
phẩm khi giá thay đổi. Thực nghiệm này có
thểcho phép sự ước lượng hệsốco giãn
theo giá
…