Baìi giaíng Pháön tæí dáùn hæåïng - Lã Cung - Bäü män Nguyãn lyï Chi tiãút maïy -Khoa Sæ phaûm kyî thuáût
33
B. ÄØ TRÆÅÜT (PALIER GLISSE)
2B.1. Khaïi niãûm chung
1. Giåïi thiãûu vãöì äø træåüt
Hçnh 2B.1 giåïi thiãûu kãút cáúu cuía mäüt loaûi äø træåüt (äø træåüt âåî) bao gäöm loït äø (2) âæåüc cäú
âënh vaìo thán äø (1). Thán äø âæåüc làõp trãn khung maïy, loït äø âæåüc làõp våïi ngoîng truûc. Trãn loït äø
coï läù (3) âãø tra dáöu bäi trån vaì raînh dáöu (4) âãø phán phäúi dáöu bäi trån trãn bãö màût loït äø.
Ngoîng truûc âæåüc làõp vaìo loït äø theo caïc kiãøu làõp coï âäü håí.
Khi truûc quay, giæîa ngoîng truûc vaì loït äø coï træåüt tæång âäúi, do âoï sinh ra ma saït træåüt trãn
bãö màût laìm viãûc cuía ngoîng truûc vaì loït äø.
2. Phán loaûi äø træåüt
(
c
)
(
1
)
: Thán ä
ø
(
2
)
: Loït ä
ø
(
4
)
Raînh dáö
u
Hçnh 2B.1 : Ä
Ø
træåüt (âåî)
(
3
)
: Läù tra dáö
u
Hçnh 2B.
2
(
b
)
Truû
N
goîng
t
r
uû
c
(
a
)
Fr
Fr
Fr
Fa
d)
Fa
Baìi giaíng Pháön tæí dáùn hæåïng - Lã Cung - Bäü män Nguyãn lyï Chi tiãút maïy -Khoa Sæ phaûm kyî thuáût
34
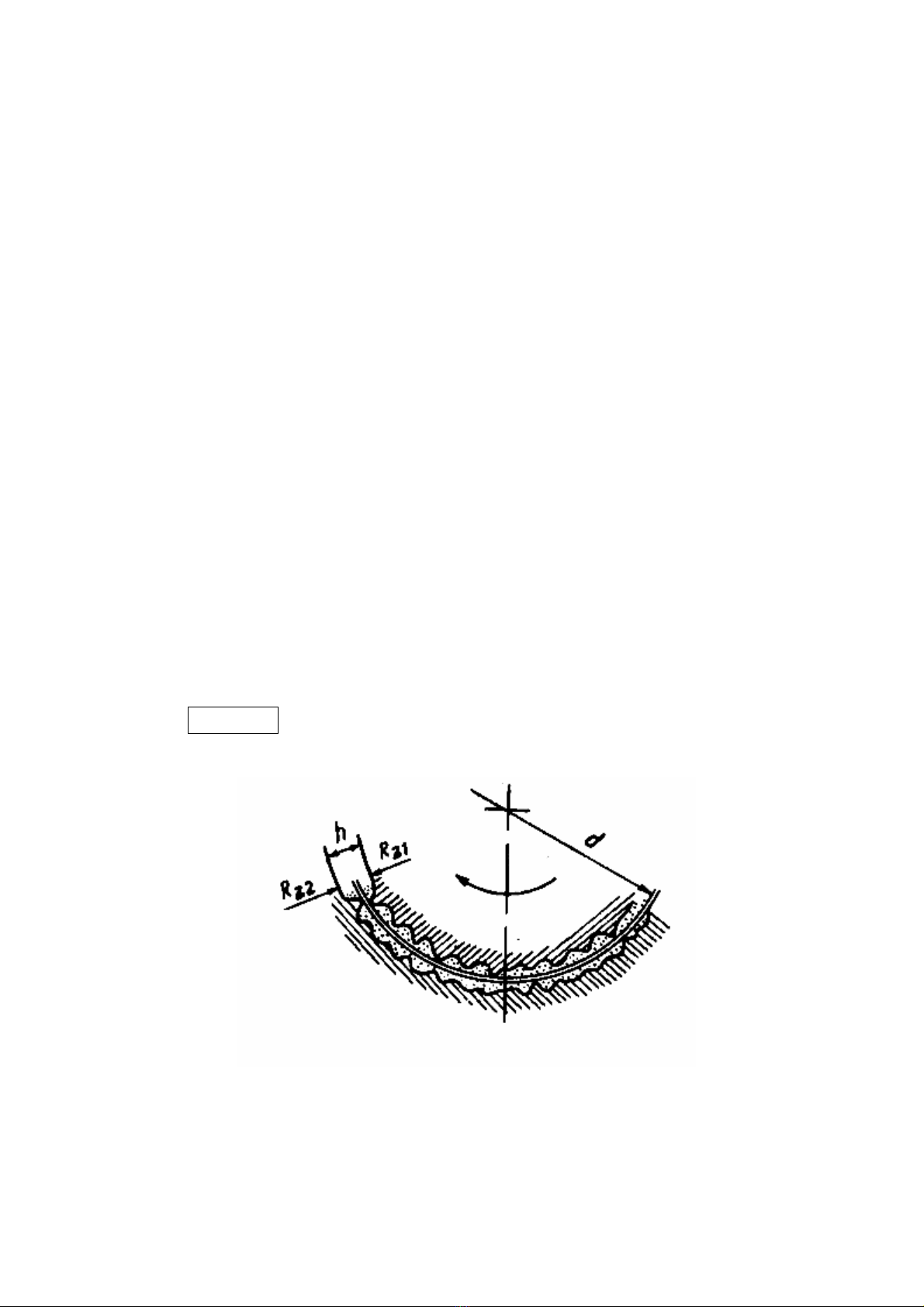
+ Theo hçnh daûng bãöö màût laìm viãûc cuía ngoîng truûc vaì loït äø chia ra : äø træåüt coï bãö màût laìm
viãûc laì màût truû (hçnh 2B.2a), màût phàóng (hçnh 2B.2b), màût cän (hçnh 2B.2c), màût cáöu (hçnh
2B.2d).
ÄØ træåüt coï bãö màût cän thæåìng chè duìng khi taíi troüng khäng låïn vaì cáön âiãöu chènh khe håí do
moìn äø, nhàòm baío âaím âäü chênh xaïc cuía cå cáúu (hçnh 2B.2c). Bãö màût cáöu êt duìng vaì våïi loaûi äø
naìy truûc coï thãø nghiãng mäüt caïch tæû do.
+ Theo khaí nàng chëu læûc chia äø træåüt thaình : äø træåüt âåî (chè chëu læûc hæåïng tám Fr) - hçnh
2B.2a, äø træåüt âåî chàûn (væìa chëu âæåüc læûc hæåïng tám Fr væìa chëu âæåüc læûc doüc truûc Fa) - hçnh
2B.2c, d, äø træåüt chàûn (chè chëu âæåüc læûc doüc truûc Fa)- hçnh 2B.2b.
Pháön låïn äø træåüt âåî, ngoaìi khaí nàng chëu læûc hæåïng tám, coï thãø chëu âæåüc læûc doüc truûc nhoí
nhåì vai truûc tç vaìo meïp äø.
ÄØ træåüt chàûn thæåìng âæåüc bäú trê laìm viãûc phäúi håüp våïi äø træåüt âåî âãø chëu âäöng thåìi læûc
hæåïng tám vaì læûc doüc truûc låïn.
+ Theo kãút cáúu äø træåüt, ta coï hai loaûi : äø nguyãn vaì äø gheïp.
+ Theo phæång phaïp bäi trån hai bãö màût laìm viãûc, phán thaình : äø bäi trån thuíy âäüng, äø bäi
trån thuíy ténh, äø bäi trån khê (taûo aïp suáút trãn bãö màût laìm viãûc bàòng khê neïn),...
2B.2. Ma saït vaì bäi trån äø træåüt
1. Caïc daûng ma saït vaì bäi trån trong äø træåüt
Âãø giaím ma saït vaì maìi moìn, cáön bäi trån äø træåüt. Tuìy theo âiãöu kiãûn bäi trån äø træåüt, coï
caïc daûng ma saït sau : æåït, næía æåït, næía khä vaì khä.
¾ Ma saït æåït
Hçnh thaình khi bãö màût ngoîng truûc vaì loït äø âæåüc ngàn caïch nhau båíi mäüt låïp dáöu bäi trån,
coï chiãöu daìy låïn hån täøng chiãöu cao caïc máúp mä bãö màût :
11zz
hR R≥+
(2B.1)
Våïi : h : chiãöu daìy låïp bäi trån, RZ1. RZ2 : chiãöu cao máúp mä bãö màût ngoîng truûc vaì loït äø.
Nhåì coï låïp dáöu bäi trån âuí daìy ngàn caïch, hai bãö màût laìm viãûc cuía ngoîng truûc vaì loït äø
khäng træûc tiãúp tiãúp xuïc våïi nhau, do âoï khäng bë moìn.
Chuyãøn âäüng tæång âäúi cuía hai bãö màût laìm viãûc bë caín tråí båíi ma saït
trong
cuía låïp dáöu bäi trån,
do âoï hãû säú ma saït æåït khaï nhoí : f = 0,001÷0,005.
¾ Ma saït næía æåït
Hçnh 2B.
3
:
Baìi giaíng Pháön tæí dáùn hæåïng - Lã Cung - Bäü män Nguyãn lyï Chi tiãút maïy -Khoa Sæ phaûm kyî thuáût
35
Hçnh thaình khi âiãöu kiãûn (2B.1) khäng thoía maîn, tæïc laì låïp bäi trån khäng âuí ngáûp caïc
máúp mä bãö màût, mäüt säú âènh máúp mä bãö màût træûc tiãúp tiãúp xuïc våïi nhau.
Hãû säú ma saït næía æåït khäng nhæîng phuû thuäüc cháút læåüng dáöu bäi trån maì coìn phuû thuäüc váût liãûu
cuía caïc bãö màût tiãúp xuïc. Hãû säú ma saït næía æåït : f = 0,008÷0,1.
¾ Ma saït næía khä vaì ma saït khä
Xaíy ra khi caïc bãö màût laìm viãûc khäng âæåüc bäi trån.
+
Ma saït khä :
laì ma saït giæîa caïc bãö màût tuyãût âäúi saûch træûc tiãúp tiãúp xuïc våïi nhau.
+
Ma saït næía khä :
Trãn thæûc tãú, duì âæåüc laìm saûch cáøn tháûn, trãn bãö màût laìm viãûc luän
luän coï nhæîng maìng khê moíng, håi áøm, hoàûc måî háúp phuû tæì mäi træåìng xung quanh, do âoï
xuáút hiãûn ma saït næía khä.
Hãû säú ma saït næía khä : f = 0,1÷0,3
Nhæ váûy äø træåüt laìm viãûc
täút nháút khi baío âaím âiãöu kiãûn bäi trån ma saït æåït
cho äø.
Chãú âäü bäi trån ma saït æåït coï thãø thæûc hiãûn bàòng hai phæång phaïp :
¾
Bäi trån thuíy ténh
: båm dáöu coï aïp suáút cao vaìo khe håí giæîa ngoîng truûc vaì loït äø, taûo ra aïp
læûc âuí låïn cán bàòng våïi taíi troüng bãn ngoaìi, náng ngoîng truûc lãn, taûo ra låïp dáöu ngàn caïch (äø
træåüt bäi trån thuíy ténh). Phæång phaïp naìy âoìi hoíi phaíi coï thiãút bë neïn vaì dáùn dáöu phæïc taûp,
nhæng âënh tám truûc âæåüc chênh xaïc, giaím moìn khi måí maïy vaì dæìng maïy.
¾
Bäi trån thuíy âäüng
: Taûo nhæîng âiãöu kiãûn cáön thiãút âãø dáöu cuäún theo ngoîng truûc vaìo khe
håí cuía äø, gáy nãn aïp suáút thuíy âäüng, taûo ra aïp læûc âuí låïn cán bàòng våïi taíi troüng bãn ngoaìi (äø
træåüt bäi trån thuíy âäüng).
2. Nguyãn lyï bäi trån thuíy âäüng
Bäi trån thuíy âäüng âæåüc thæûc hiãûn theo nguyãn lyï sau âáy:
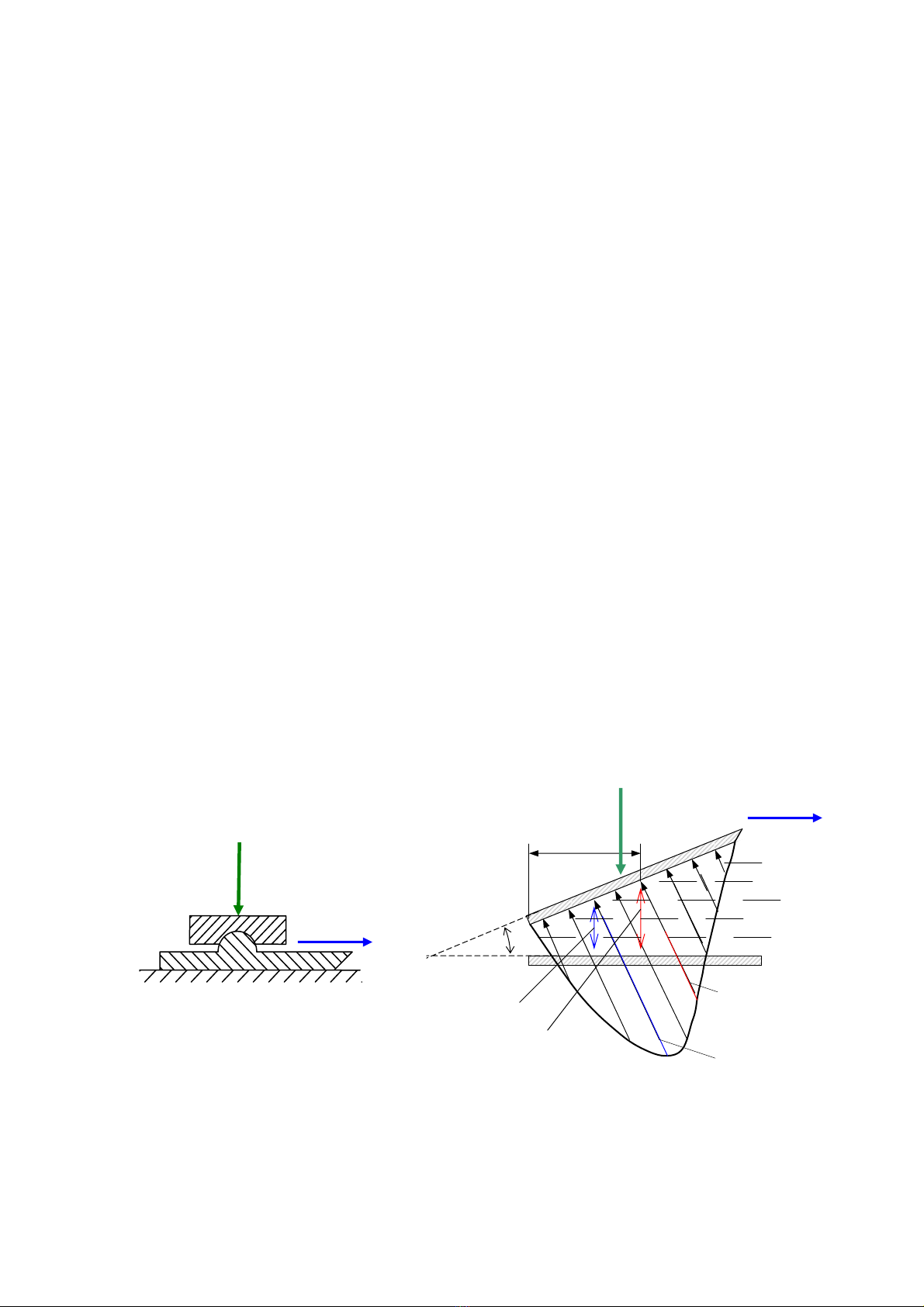
Xeït hai táúm phàóng A vaì B, ngám trong dáöu, nghiãng våïi nhau mäüt goïc α naìo âoï, chëu taïc
âäüng cuía mäüt læûc Fr. Chiãöu daìi caïc táúm theo phæång vuäng goïc våïi màût phàóng hçnh veî xem
nhæ vä haûn. Dáöu coï âäü nhåït âäüng læûc laì µ. Táúm A chuyãøn âäüng so våïi táúm B våïi váûn täúc laì v
(hçnh 2B.4b).
Khi chæa chuyãøn âäüng, táúm A seî bë eïp chàût vaìo táúm B (hçnh 2B.4a).
Khi táúm A chuyãøn âäüng, låïp dáöu dênh vaìo bãö màût táúm A seî bë keïo theo. Nhåì coï âäü nhåït,
caïc låïp dáöu phêa dæåïi cuîng chuyãøn âäüng theo. Dáöu bë däön vaìo pháön heûp cuía khe håí hçnh
chãm, bë neïn laûi, taûo nãn aïp suáút dæ.
v
Fr
A
B
Hçnh 2B.4
a
α
B
A
p
max
p
x
h
h0
Hçnh 2B.4
b
Fr
v
Baìi giaíng Pháön tæí dáùn hæåïng - Lã Cung - Bäü män Nguyãn lyï Chi tiãút maïy -Khoa Sæ phaûm kyî thuáût
36
Khi váûn täúc v âuí låïn (v > vgh), táúm A âæåüc náng hàón lãn, giæîa hai táúm coï låïp dáöu ngàn
caïch, chãú âäü bäi trån ma saït æåït âaî âæåüc hçnh thaình (hçnh 2B.4b).
AÏp suáút thuíy âäüng p (aïp suáút dæ) trong låïp dáöu nàòm giæîa hai táúm (coìn goüi laì
chãm dáöu
)
âæåüc xaïc âënh theo phæång trçnh Reynolds :
0
3
dp h - h
6. .v
dx h
=µ (2B.2)
våïi : µ : âäü nhåït âäüng læûc cuía dáöu bäi trån
v : váûn täúc chuyãøn âäüng cuía táúm A so våïi táúm B
h : khe håí taûi vë trê coï toüa âäü x, coï aïp suáút p
h0 : khe håí taûi vë trê coï aïp suáút låïn nháút pmax
AÏp suáút dæ taûi cæía vaìo vaì cæía ra bàòng 0.
AÏp suáút cæûc âaûi taûi tiãút diãûn coï h = ho, luïc âoï : dp 0
dx
=
.
AÏp suáút dæ noïi trãn taûo nãn mäüt aïp læûc cán bàòng våïi taíi troüng Fr taïc âäüng lãn táúm A.
Tæì (2B.2), ta tháúy aïp suáút p caìng låïn khi µ, v caìng låïn, nghéa laì khaí nàng taíi cuía chãm dáöu
caìng låïn.
Toïm laûi,
âiãöu kiãûn âãø hçnh thaình maìng dáöu bäi trån ma saït æåït
bàòng phæång phaïp thuíy
âäüng :
+ Giæîa hai bãö màût træåüt phaíi coï khe håí hçnh chãm
+ Dáöu phaíi coï âäü nhåït nháút âënh vaì liãn tuûc chaíy vaìo khe håí hçnh chãm
+ Váûn täúc tæång âäúi giæîa hai bãö màût træåüt phaíi coï phæång, chiãöu thêch håüp vaì trë säú âuí låïn
âãø aïp suáút sinh ra trong chãm dáöu cán bàòng âæåüc våïi taíi troüng bãn ngoaìi.
Våïi kãút cáúu khäng coï khe håí hçnh chãm, nhæ træåìng håüp äø træåüt chàûn trãn hçnh 2B.2b thç
khäng thãø taûo ra bäi trån ma saït æåït bàòng phæång phaïp thuíy âäüng âæåüc. Khi âoï cáön phaíi coï
caïc biãûn phaïp vãö kãút cáúu âãø taûo ra khe håí hçnh chãm.
Våïi äø træåüt âåî, khe håí hçnh chãm hçnh thaình tæû nhiãn nhåì âæåìng kênh ngoîng truûc d nhoí
hån âæåìng kênh loït äø D vaì tám ngoîng truûc nàòm lãûch so våïi tám loït äø (hçnh 2B.5a).
3. Khaí nàng taíi cuía äø træåüt (äø træåüt âåî)
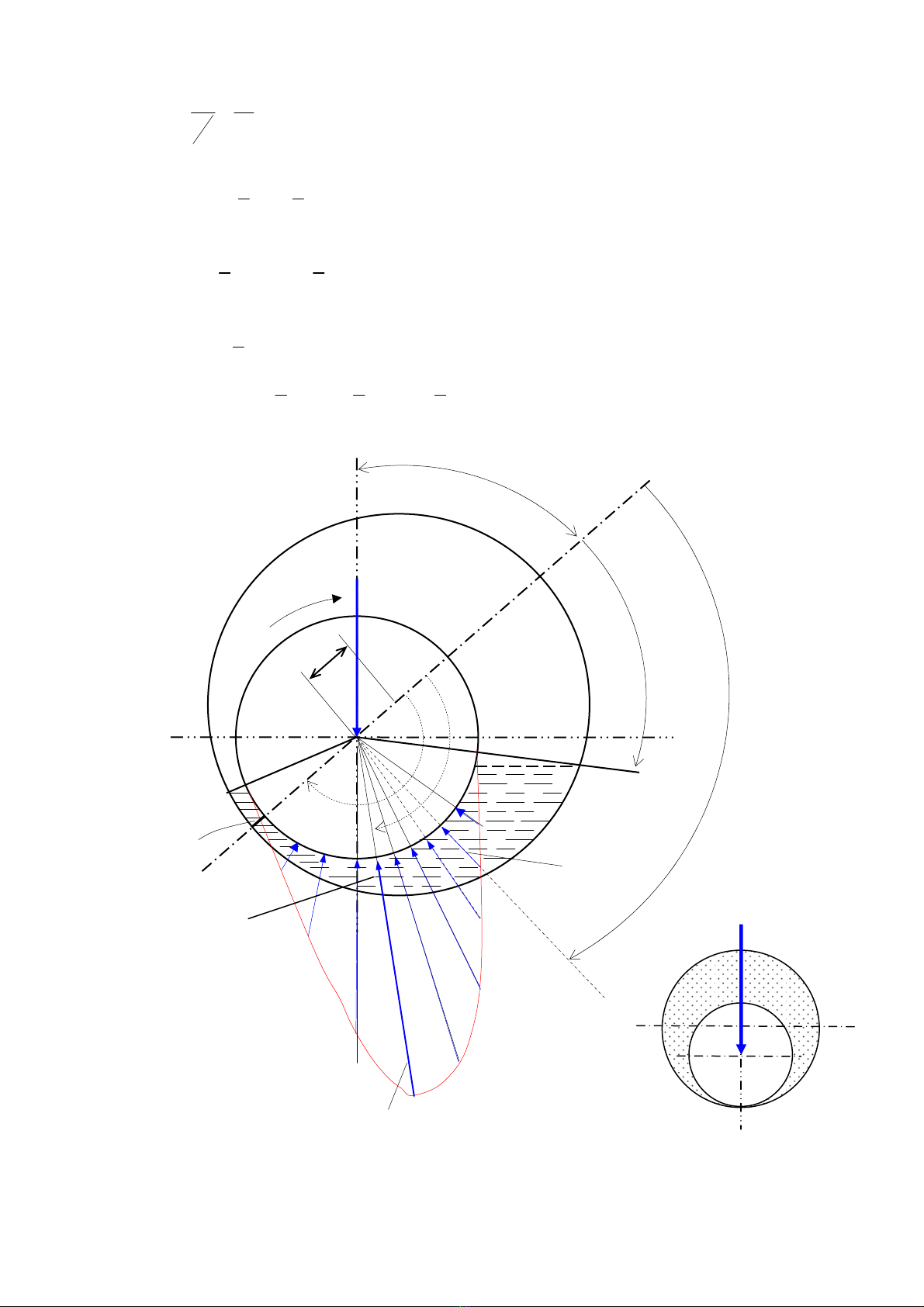
Xeït äø træåüt âåî trãn hçnh 2B.5, ngoîng truûc chëu taíi troüng hæåïng tám Fr.
Khi truûc chæa quay, dæåïi taïc duûng cuía læûc Fr, ngoîng truûc tiãúp xuïc våïi loït truûc taûi âiãøm I
trãn phæång taïc duûng cuía læûc Fr.
Khi truûc quay våïi váûn täúc goïc ω, ngoîng truûc cuäún dáöu vaìo khe håí hçnh chãm, dáöu bë neïn
laûi vaì taûo nãn aïp suáút thuíy âäüng. Khi váûn täúc ω âaût giaï trë cáön thiãúút thç aïp suáút thuíy âäüng âuí
låïn, taûo nãn aïp læûc cán bàòng âæåüc våïi taíi troüng Fr, truûc âæåüc náng hàón lãn vaì chãú âäü bäi trån
ma saït æåït âæåüc hçnh thaình.
Âãø xaïc âënh aïp suáút thuíy âäüng trong äø træåüt âåî, ta duìng hãû toüa âäü cæûc (r, ϕ) trãn hçnh
2B.5a.
Kyï hiãûu :
Ddδ= − : âäü håí hæåïng kênh våïi D : âæåìng kênh loït äø, d : âæåìng kênh ngoîng truûc
Dd
dd
−δ
ψ= = : âäü håí tæång âäúi
e = O1O2 : âäü lãûch tám
Baìi giaíng Pháön tæí dáùn hæåïng - Lã Cung - Bäü män Nguyãn lyï Chi tiãút maïy -Khoa Sæ phaûm kyî thuáût
37
e2e
2
χ= =
δδ : âäü lãûch tám tæång âäúi
⇒ Chiãöu daìy nhoí nháút cuía låïp dáöu :
()
min
he1
22
δδ
=−= −χ
Chiãöu daìy cuía låïp dáöu æïng våïi æïng våïi goïc ϕ :
()
h e cos 1 cos
22
δδ
=+ ϕ= +χ ϕ
Chiãöu daìy låïp dáöu æïng våïi goïc ϕ0 taûi âoï coï p = pmax :
()
00
h1cos
2
ϕ
δ
=+χϕ
Màût khaïc : d
v2
=ω
; d
dx d
2
=ϕ
; d
δ
ψ
=
Tæì âoï coï thãø viãút laûi phæång trçnh Reynold (2B.2) trong hãû toüa âäü cæûc nhæ sau :
A
B
pmax
hmin
hϕ0
p
(ϕ)
ϕ
1
ϕ
ϕa
e
ϕ
0
ϕ
2
O1
O2
ω
Hçnh 2B.5
b
Hçnh 2B.5
a
I
Fr