BÀI:
-8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10
-3
-2
-1
1
2
3
4
5
6
7
8
x
y
y=f
1
(x)=2|x|
y=f
2
(x)=|2x-4|
A. M C ĐÍCH – YÊU C U:Ụ Ầ
1. Ki n th c: ế ứ
-Giúp sinh viên hi u rõ tính ch t và n m đ c các d ng đ th hàm s .ể ấ ắ ượ ạ ồ ị ố
-Giúp cho sinh viên n m đ c các phép suy lu n đ th (phép đ i x ng – ắ ượ ậ ồ ị ố ứ
phép t nh ti n).ị ế
-Qua đó giúp sinh viên gi ng d y t t các n i dung có liên quan trong ả ạ ố ộ
ch ng trình toán ph thông.ươ ổ
2. K năng:ỹ
- Xác đ nh đ c các phép suy lu n đ th .ị ượ ậ ồ ị
- V đ c các d ng đ th hàm s .ẽ ượ ạ ồ ị ố
- Rèn luy n kĩ năng ra đ ki m tra có liên quan đ n n i dung này.ệ ề ể ế ộ
3. Thái đ :ộ
Thái đ nghiêm túc, tích c c, ch đ ng trong h c t p.ộ ự ủ ộ ọ ậ
B. N I DUNG:Ộ
1Đ TH HÀM S CH A D U Ồ Ị Ố Ứ Ấ
GIÁ TR TUY T Đ IỊ Ệ Ố
2 PHÉP SUY ĐỒ THỊ
(PHÉP ĐỐI XỨNG - PHÉP TỊNH TIẾN)
Đ xác đ nh đ th c a hàm s có ch a giá tr tuy t đ i (trong ể ị ồ ị ủ ố ứ ị ệ ố
nh ng tr ng h p khác), thì ta b d u giá tr tuy t đ i. Khi đó ta ữ ườ ợ ỏ ấ ị ệ ố
đ c hàm s đ c cho b i nhi u công th c. Đ th hàm s này ượ ố ượ ở ề ứ ồ ị ố
g m nhi u ph n, m i ph n ng v i đ th c a t ng hàm s t o ồ ề ầ ỗ ầ ứ ớ ồ ị ủ ừ ố ạ
thành trên m t t p h p xác đ nh. ộ ậ ợ ị
L u ý:ư
( )
( ), 0y f x f x x= =
2. V i ớvà đây là hàm s ch n nên đ ố ẵ ồ
th đ i x ng qua ị ố ứ Oy. Do v y ta có: ậ
1. V i ớ( ), ( ) 0
( ) ( ), ( ) 0
f x f x
y f x f x f x
= = − <
nên ta có:
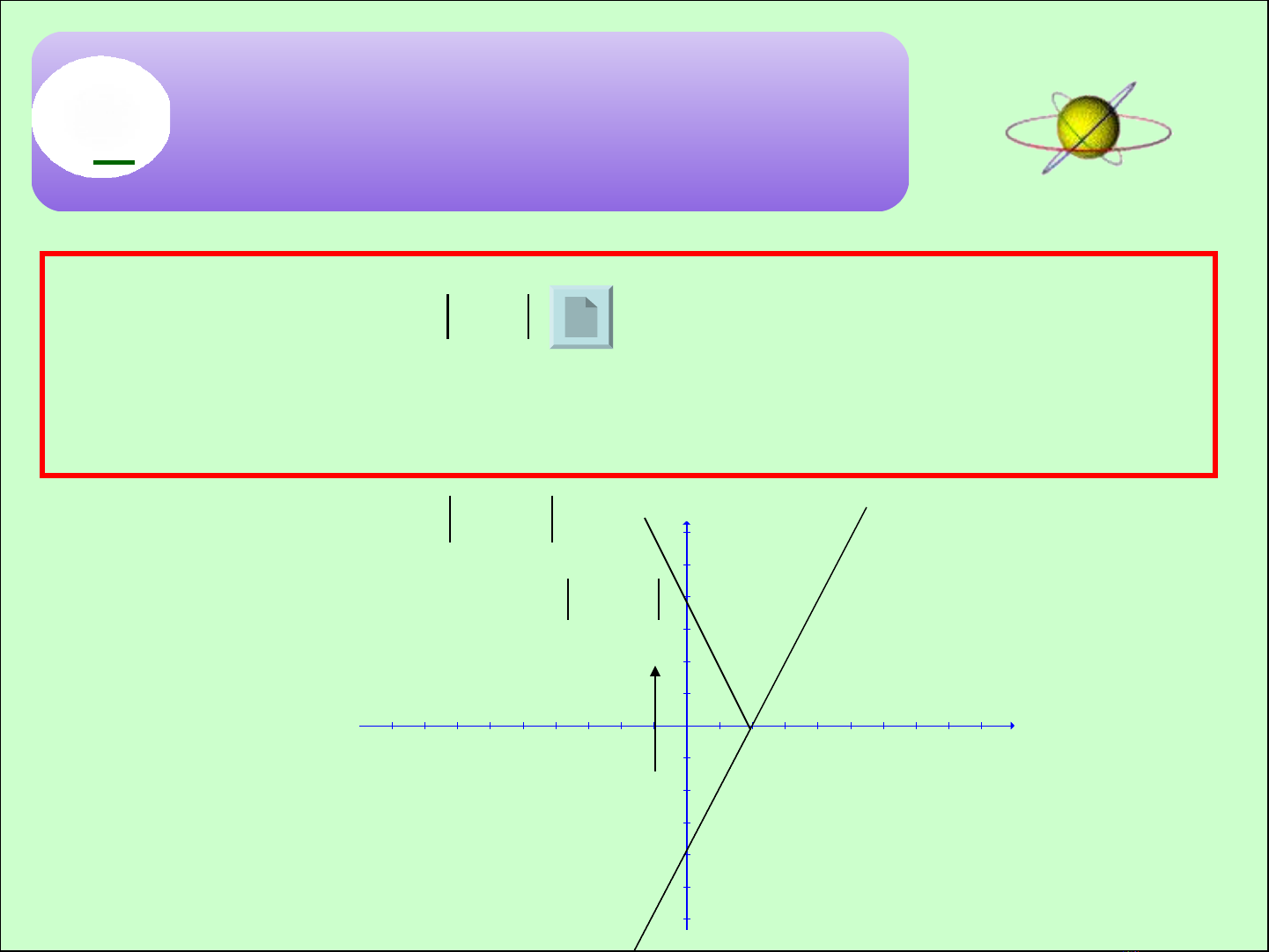
1Đ TH HÀM S CH A D U Ồ Ị Ố Ứ Ấ
GIÁ TR TUY T Đ IỊ Ệ Ố
1. Đ th hàm s :ồ ị ố
( )y f x
=
Ph n 1: Là ph n đ th ầ ầ ồ ị y = f(x) ng v i ứ ớ
0y
Ph n 2: Là ph n đ i x ng qua ầ ầ ố ứ Ox c a ph n đ th ủ ầ ồ ị y = f(x) ng v i ứ ớ y < 0
VD: Đ th hàm s ồ ị ố
2 4y x= −
-9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
x
y
y=2x-4
2 4y x= −
G m hai ph n:ồ ầ