TÀI LIỆU HƯỚNG DẪN MÔN HỌC CƠ HỌC KẾT CẤU
Mục tiêu:
+Nắm vững quy ước dấu của nội lực trong thanh.
+Nắm vững cách xác định nội lực tại một mặt cắt ngang.
+Nắm vững phương pháp vẽ biểu đồ theo từng điểm.
Nhắc nhở thân thiện:
+Đọc chậm từng bước và xem kĩ hình vẽ để nắm vững cách làm.
+ Tham khảo thêm Chương 2giáo trình Sức bền vật liệu,thầy Đỗ Kiến Quốc (Chủ
biên) và các tác giả khác, NXB ĐHQG TP.HCM.
+Mọi thắc mắc xin vui lòng liên hệ:
Email: ceac.xdbk@gmail.com
Fanpage: Học thuật Xây dựng Bách Khoa (facebook.com/hocthuatxaydung)
Group: Diễn đàn Cơ sở ngành Xây Dựng (facebook.com/groups/thogiaichuyennghiep)
CEAC – Học thuật Xây dựng Bách Khoa 3
Vấn đề 1:
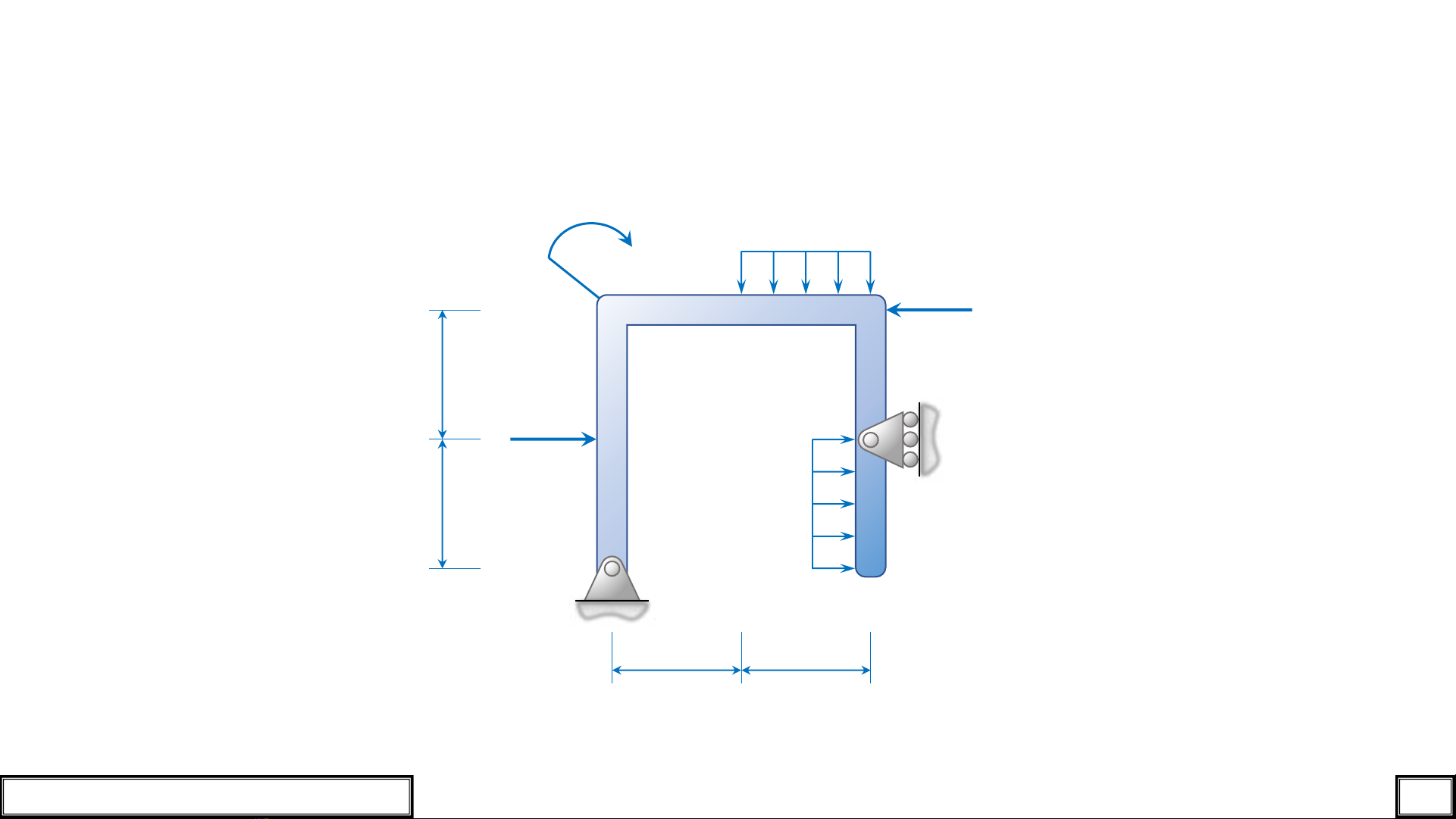
Cho hệ khung ABCDE chịu tác dụng của các tải trọng như hình vẽ (bỏ qua trọng lượng
bản thân kết cấu):
Vẽ biểu đồ nội lực trong hệ khung.
Hình 1.1
A
qL2
L L
B
L
L
q
qL
q
qL
C
D
E
CEAC – Học thuật Xây dựng Bách Khoa 4
Lời giải tham khảo:
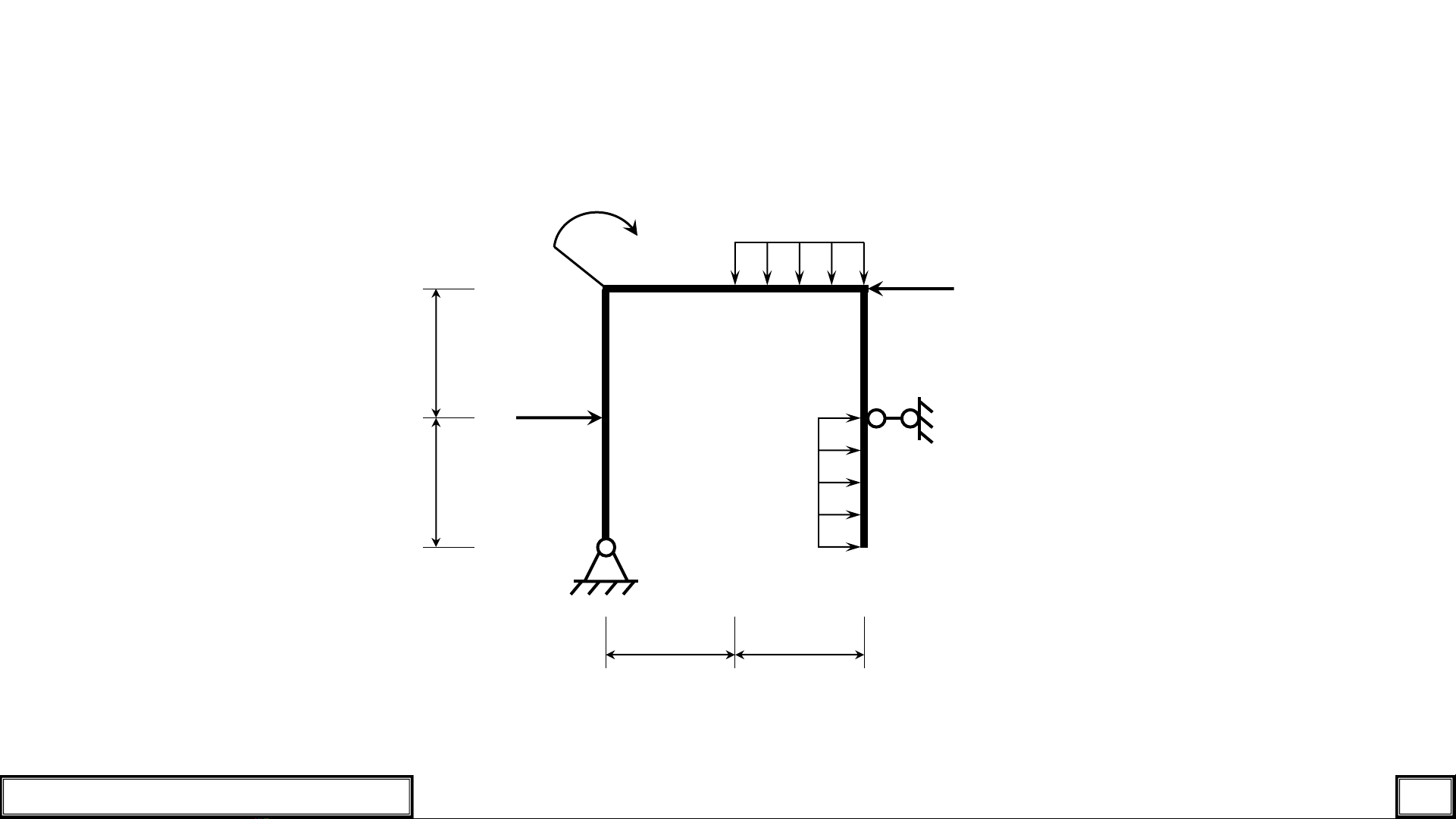
Hình 1.2
Bước 1:
Lập sơ đồ tính.
A
qL2
L L
B
L
L
q
qL
q
qL
C
D
E
CEAC – Học thuật Xây dựng Bách Khoa 5
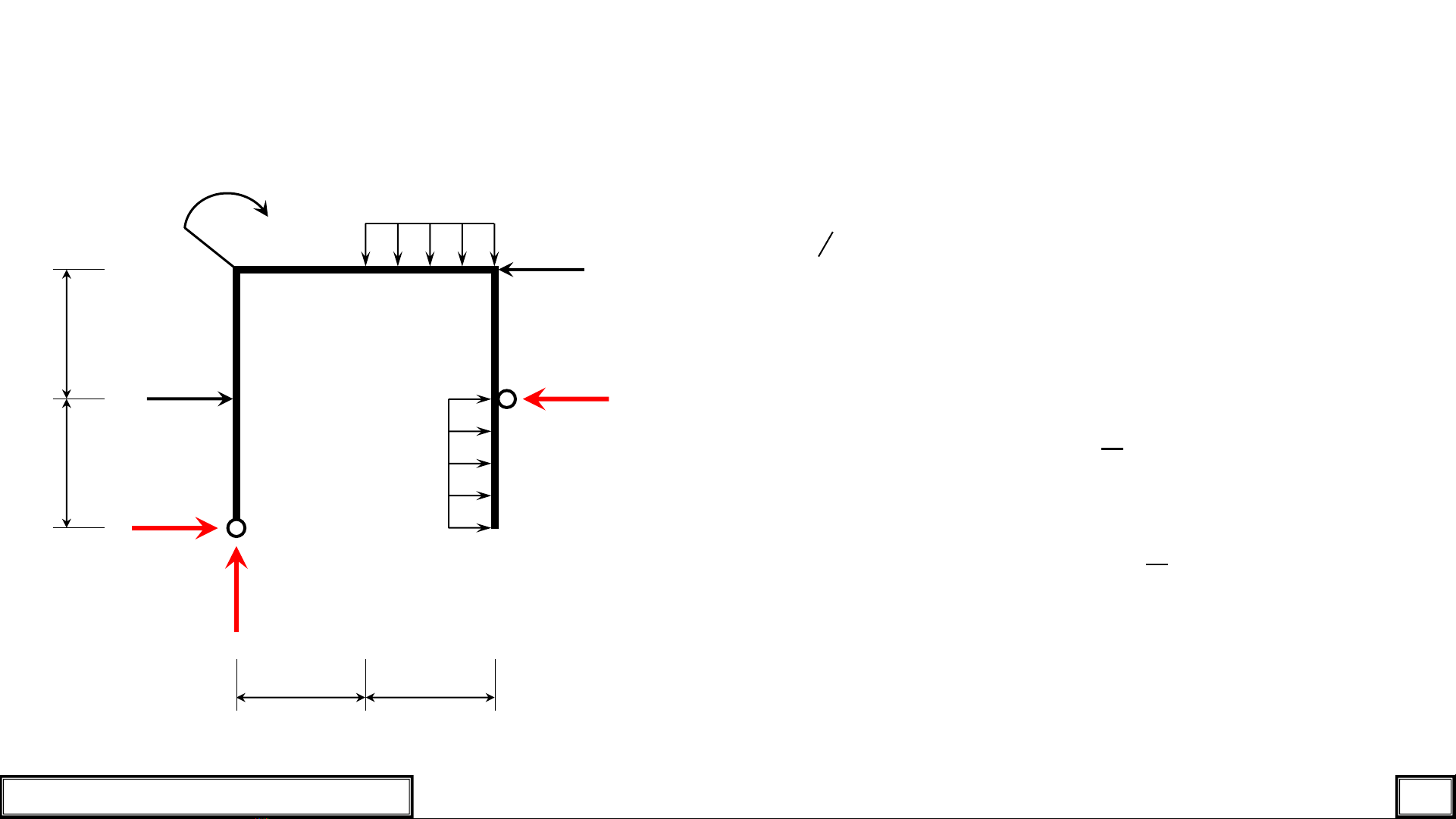
Bước 2:
Xác định phản lực liên kết.
Hình 1.3
A
qL2
L L
B
L
L
q
qL
q
qL
C
D
E
VA
HA
HD
0
0
0
x
y
A
F
F
M
=
=
=
( )
( )
( ) ( )
2
0
0
32
2
AD
A
H qL qL q L H
V q L
qL L qL qL L qL L
+ − + − =
− =

− − − +


2
A
A
D
H qL
V qL
H qL
=
=
=
( )
10
2D
qL L H L

− + =


Giải hệ phương trình cân bằng lực: