Tiết 1 : BÀI: GIỚI HẠN CỦA DÃY SỐ

Chia sẻ: Abcdef_47 Abcdef_47 | Ngày: | Loại File: PDF | Số trang:5

Thêm vào BST

Báo xấu

135
lượt xem 19
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Định nghĩa giới hạn hữu hạn của dãy số. Về kỹ năng: Tìm giới hạn dãy số sử dụng định nghĩa và tính chất Về thái độ: cẩn thận và chính xác. II/ Chuẩn bị: Học sinh: Ôn tập kiến thức dãy số và nghiên cứu bài mới. Giáo viên: giáo án, bảng phụ, phiếu học tập. Phương tiện: phấn và bảng.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Tiết 1 : BÀI: GIỚI HẠN CỦA DÃY SỐ

Tiết 1 : BÀI: GIỚI HẠN CỦA DÃY SỐ I/ Mục tiêu: Giúp học sinh nắm được : Về kiến thức: Định nghĩa giới hạn hữu hạn của dãy số. Về kỹ năng: Tìm giới hạn dãy số sử dụng định nghĩa và tính chất Về thái độ: cẩn thận và chính xác. II/ Chuẩn bị: Học sinh: Ôn tập kiến thức dãy số và nghiên cứu bài mới. Giáo viên: giáo án, bảng phụ, phiếu học tập. Phương tiện: phấn và bảng. III/ Phương pháp: gợi mở , vấn đáp. IV/ Tiến trình bài học: 1 Kiểm tra bài cũ: Cho dãy số (un) với un = . Viết các số hạng u10, u20, u30, u40, u50,u60 1. n u70, u80,u90, u100? Nội dung bài mới: 2. Hoạt động của học sinh Hoạt động của giáo viên Phần ghi bảng
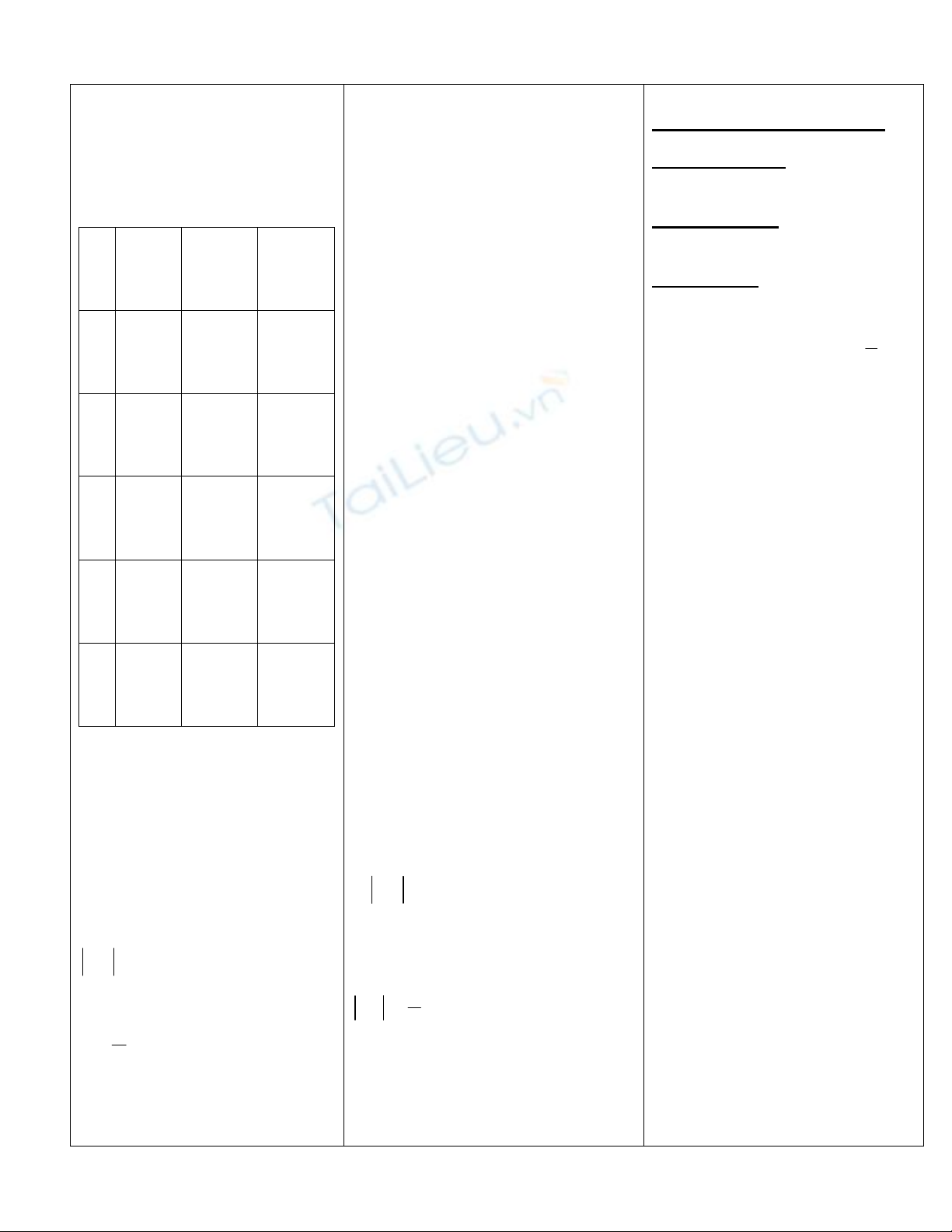
Thực hành hoạt động 1 I. GIỚI HẠN HỮU HẠN CỦA DÃY SỐ Lập bảng giá trị của un khi n nhận các giá trị 10, 20, 30, 40, 1) Định nghĩa: 50, 60, 70, 80, 90. (viết un dưới n 10 20 30 Hoạt động 1 dạng số thập phân, lấy bốn chữ số thập phân) 1 un 0,1 0,05 0,0333 Cho dãy số (un) với un = n GV: Treo bảng phụ hình biểu a) Nhận xét xem khoảng cách diễn (un) trên trục số n 40 50 60 từ un tới 0 thay đổi như thế nào khi trở nên rất lớn. uu 0,025 0,02 0,0167 b) Bắt đầu từ số hạng un nào đó của dãy số thì khoảng cách n 70 80 90 từ un đến 0 nhỏ hơn 0,01? 0,001? un 0,014 0,0125 0,0111 Cho học sinh thảo luận và trả TLời lời câu a) a) Khoảng cách từ un tới 0 Khi n trở nên rất lớn thì càng rất nhỏ. khoảng cách từ un tới 0 càng b) Bắt đầu từ số hạng u100 trở un  0,01 ? rất nhỏ. 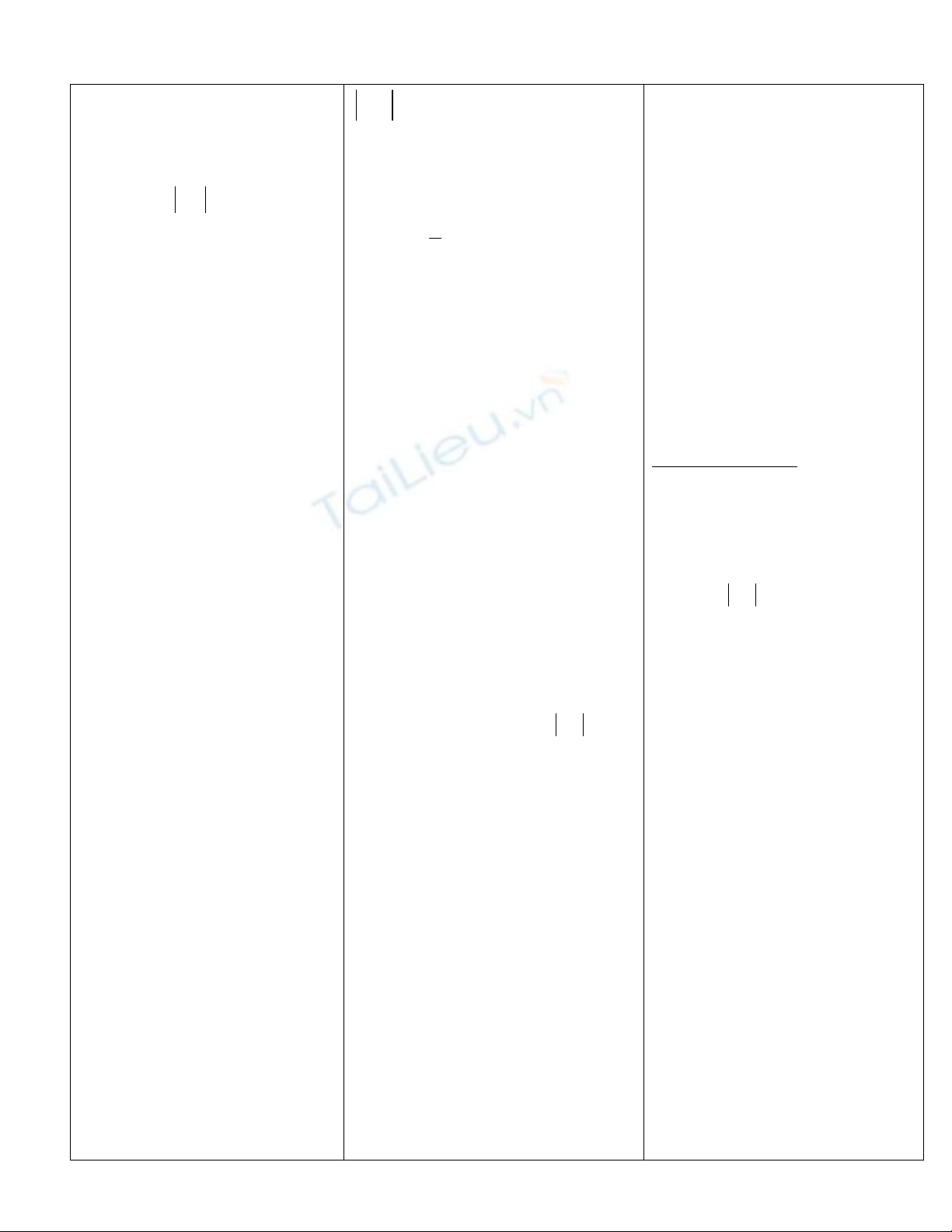đi thì khoảng cách từ un đến 0 Ta cũng chứng minh được rằng un  0,01 nhỏ hơn 0,01 1 un  có thể nhỏ hơn một số Bắt đầu từ số hạng u1000 trở đi n 1   0,01  n  100 thì khoảng cách từ un đến 0 dương bé tuỳ ý, kể từ một số n nhỏ hơn 0,001 hạng nào đó trở đi, nghĩa là Bắt đầu từ số hạng u100 trở đi
thì khoảng cách từ un đến 0 u n có thể nhỏ hơn bao nhiêu nhỏ hơn 0,01 cũng được miễn là chọn n đủ lớn. Khi đó ta nói dãy số (un) un  0,001 Tương tự 1 với un = có giới hạn là 0 khi n n  n  1000 dần tới dương vô cực. Từ đó cho học sinh nêu đ/n dãy số có giới hạn là 0. G/v chốt lại đ/n ĐỊNH NGHĨA 1 Ta nói dãy số (un) có giới hạn là 0 khi n dần tới dương vô cực nếu u n có thể hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi. Giải thích thêm để học sinh hiểu VD1. Và nhấn mạnh: “ u n có Kí hiệu: nlim u n  0 hay   thể hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi. H/s trả lời có thể thiếu chính u n  0 khi n   xác Có nhận xét gì về tính tăng, giảm và bị chặn của dãy số ở HĐ1 và ở VD1? Đọc hiểu Ví dụ 1 (SGK)
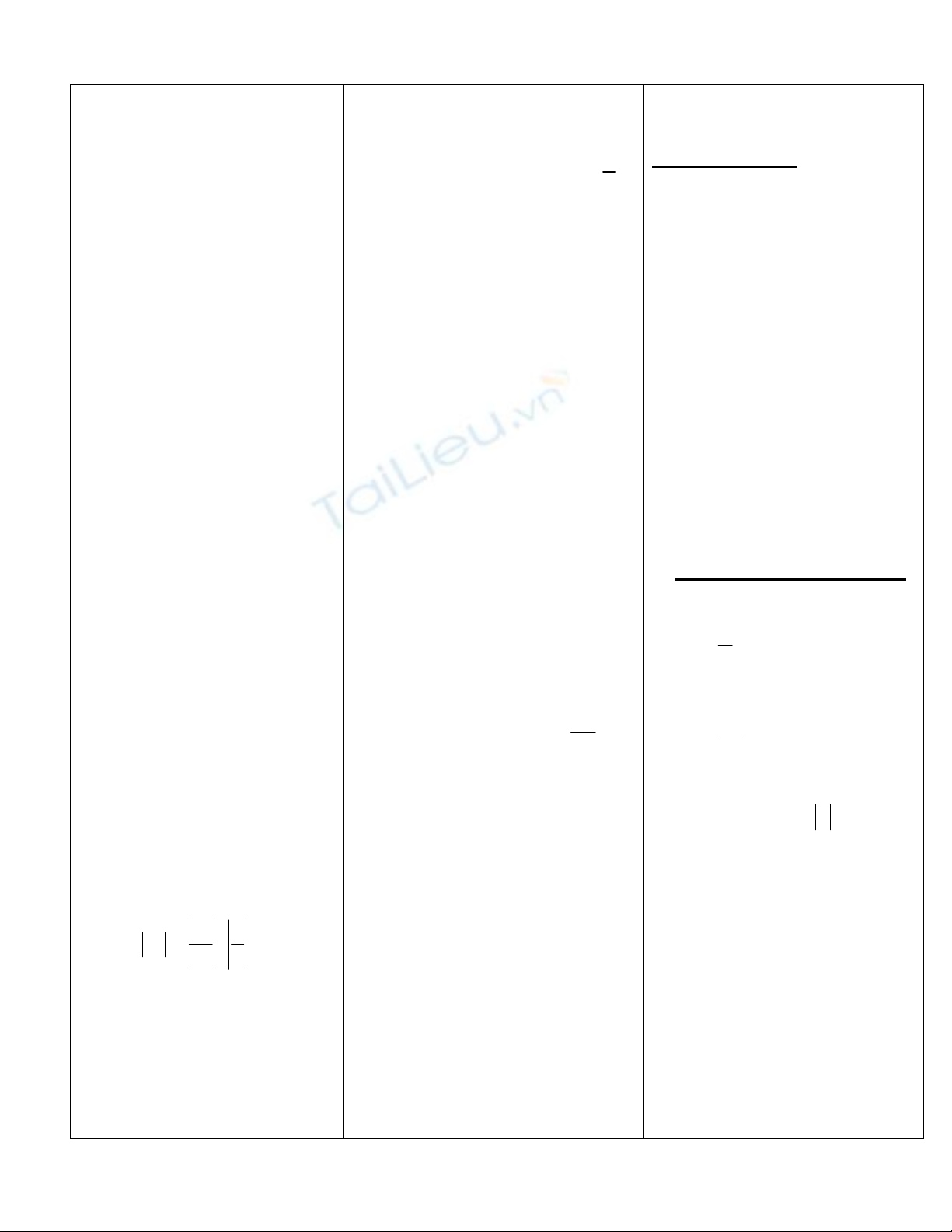
ĐỊNH NGHĨA 2 1 Cho dãy số (un) với u n  2  n Ta nói dãy số (vn) có giới hạn Dãy số này có giới hạn như thế là số a (hay vn dần tới a) khi Dãy số ở HĐ1 là dãy giảm nào? n   , nếu lim v n  a   0 n   và bị chặn, còn dãy số ở Để giải bài toán này ta nghiên VD1 là dãy không tăng, Kí hiệu: nlim v n  a hay cứu ĐN2   không giảm và bị chặn vn  a khi n   Dãy số này có giới hạn là 2 2) Một vài giới hạn đặc biệt GV giải thích thêm sự vận dụng 1 0; a) nlim Đ/n 2 trong c/m của ví dụ 2 n   1 1 Cho dãy số (un) với un = ,  o ,  k  Z lim nk n  n k k  Z  Dãy số này có giới hạn Đọc hiểu Ví dụ 2 (SGK) b) nlim q n  0 nếu q  1   ntn? c) Nếu un = c (c là hằng số) thì nlim u n  a  nlim c  c 11 n  N * Ta có: u n       k n n CHÚ Ý Do đó dãy số này có giới hạn Từ nay về sau thay cho là 0 lim u n  a , ta viết tắt là n  
lim un = a Lúc này dãy có giới hạn là c Nếu un = c (c là hằng số)? * Vì u n  c  0  n  N V/ CŨNH CỐ, DẶN DÒ: Đ/n giới hạn hữu hạn của dãy số: “|un| có thể nhỏ hơn một số dương tuỳ ý, kể từ một số hạng nào đó trở đi”. Các tính chất về giới hạn hữu hạn. Ôn tập kiến thức và làm bài tập SGK