Vật lý hiện đại: Chương 3 (modern physics)

1

Ch−¬ng III: Nguyªn tö

3.1

3.1 Nguyªn tö vµ c¸c tÝnh chÊt cña nguyªn tö

Nguyªn tö vµ c¸c tÝnh chÊt cña nguyªn tö

Nguyên tử là gì?

Nguyên tử là những block cơ bản của vật chất, xây dựng

nên tất cả mọi vật xung quanh chúng ta. Cái bảng, không

khí và ngay cả chúng ta đều được cấu tạo từ những

nguyên tử.

Người ta đã tìm ra được 90 loại nguyên tử tồn tại tự nhiên

và các nhà khoa học đã chế tạo ra được quãng 25 loại

trong các phòng thí nghiệm.

Ngày 23/07/2004 đã phát hiện ra nguyên tố thứ 113 tại

Riken, Nhật bản.

Nguyên tử là gì?

Nguyên tử là những block cơ bản của vật chất, xây dựng

nên tất cả mọi vật xung quanh chúng ta. Cái bảng, không

khí và ngay cả chúng ta đều được cấu tạo từ những

nguyên tử.

Người ta đã tìm ra được 90 loại nguyên tử tồn tại tự nhiên

và các nhà khoa học đã chế tạo ra được quãng 25 loại

trong các phòng thí nghiệm.

Ngày 23/07/2004 đã phát hiện ra nguyên tố thứ 113 tại

Riken, Nhật bản.

2

Một sốtÝnh chÊt của nguyªn tử:

a. C

Cá

ác nguy

c nguyê

ên t

n tử

ửđượ

được s

c sắ

ắp x

p xế

ếp theo m

p theo mộ

ột s

t sơ

ơđồ

đồ h

hệ

ệth

thố

ống

ng.

.

b. C

Cá

ác nguy

c nguyê

ên t

n tử

ửph

phá

át x

t xạ

ạv

và

àh

hấ

ấp th

p thụ

ụá

ánh s

nh sá

áng.

ng. Tần sốvcủa ánh

sáng được phát xạ(hấp thụ) đáp ứng điều kiện tần sốcủa Bohr:

hv = Ej–E

k

c. C

Cá

ác nguy

c nguyê

ên t

n tử

ửc

có

ómoment xung l

moment xung lượ

ượng v

ng và

àt

từ

ừt

tí

ính.

nh.

3

2

4

§å thÞ biÓu diÔn n¨ng l−îng ion hãa

5

3.2

3.2 Ph−¬ng tr×nh Schr

Ph−¬ng tr×nh SchrÖ

Ödinger (SE)

dinger (SE)

vµ nguyªn tö Hydro

→

→SE

SE -

-L

Là

àđị

định

nh đề

đề c

cơ

ơb

bả

ản c

n củ

ủa QM thay v

a QM thay và

ào ch

o chổ

ổc

củ

ủa c

a cá

ác

c đị

định

nh

lu

luậ

ật chuy

t chuyể

ển

n độ

động c

ng củ

ủa Newton trong th

a Newton trong thế

ếgi

giớ

ới l

i lượ

ượng t

ng tử

ử.

.

C

Cá

ác y

c yê

êu c

u cầ

ầu c

u cơ

ơb

bả

ản

n đố

đối v

i vớ

ới ph

i phươ

ương tr

ng trì

ình Schrodinger

nh Schrodinger

¾phải là phương trình chứa đạo hàm của theo thời gian của

hàm sóng, bởi nó mô tảsựphụthuộc theo thời gian của hàm

sóng.

¾phải là phương trình tuyến tính bởi nếu như

ψ

1 và ψ2là lời giải

của phương trình, thì tổhợp tuyến tính c1

ψ

1+c2

ψ

2cũng phải là

lời giải của phương trình.

¾các hệsốkhông được chứa các thành phần phụthuộc vào

trạng thái nhưnăng lượng, moment xung lượng…, nếu không

sựáp dụng của phương trình sẽbịgiới hạn.

6

Ta đã có hàm sóng đối với hạt tự do:

()

)(

0

,rptE

i

p

P

etr

rr

h

r−−

Ψ=Ψ

ψ

E

i

t

h

−=

∂

ψ

h

x

ip

x

−=

∂

ψ

2

h

x

p

x

−=

∂

ψψ

ψψψ

2

h

p

zyx −=∇=

∂

+

∂

+

∂

⇒

3

7

Ta thấy phương trình này đáp ứng được các yêu cầu

đối với SE.

Nhận thấy:

→Các toán tử này là toán tử năng lượng và moment

m

p

E2

2

=

ψ

2

2∇−=

∂

m

t

ih

h

∇−→

∂

→h

r

hip

t

iE ,

⇒

8

Nếu khi

Nếu khi hạt không tự do

hạt không tự do và nằm trong trường

và nằm trong trường

thế

Ta có

Ph

Phươ

ương tr

ng trì

ình n

nh nà

ày do nh

y do nhà

àb

bá

ác h

c họ

ọc ng

c ngườ

ười

i Á

Áo Ervin

o Ervin

Schrodinger

Schrodinger đư

đưa ra

a ra đầ

đầu ti

u tiê

ên n

n nă

ăm 1926.

m 1926.

()

rU r

)(

2

rU

m

p

Er

+=

()

ψψ

ψ

rU

m

t

ir

h

h+∇−=

∂

∂2

2

⇓

Hàm thếnăng

của hệ

Hàm thếnăng

của hệp.t. Schrodinger

p.t. Schrodinger

-Hàm sóng

-Năng lượng

-Moment xung

lượng

- Moment từ

-Hàm sóng

-Năng lượng

-Moment xung

lượng

-Moment từ

→

9

3.3

3.3 N¨ng l−îng cña c¸c tr¹ng th¸i

N¨ng l−îng cña c¸c tr¹ng th¸i

cña nguyªn tö hydro

Với n =1, 2, 3 …. là các sốnguyên và được gọi là

s

số

ốl

lượ

ượng t

ng tử

ửch

chí

ính.

nh.

eV

nn

E

nh

me

En22

1

222

0

46,131

.

8−=−=













−=

ε

4

10

3.4

3.4 Moment quü ®¹o vµ tõ tÝnh

Moment quü ®¹o vµ tõ tÝnh



độ

độl

lớ

ớn c

n củ

ủa moment qu

a moment quỹ

ỹđạ

đạo b

o bằ

ằng

ng

v

vớ

ới

i



đượ

được g

c gọ

ọi l

i là

às

số

ốl

lượ

ượng t

ng tử

ửqu

quỹ

ỹđạ

đạo

o



=

= 0, 1, 2, 3

0, 1, 2, 3…

…(

(n

n -

-1)

1)

l

hll )1( +=L

π

2

h

=h

l

Số lượng tử từ

Số lượng tử từl

m

•

•độ lớn của vectơ trên trục

độ lớn của vectơ trên trục z

z:

:

L

r

h

l

mLz=

l

m

•

•l

là

às

số

ốl

lượ

ượng t

ng tử

ửt

từ

ừ, n

, nó

óch

chỉ

ỉc

có

óth

thể

ểnh

nhậ

ận

n đượ

được c

c cá

ác gi

c giá

átr

trị

ị:

:

l

l±±±= ,....2,1,0m

•

•S

Sự

ựh

hạ

ạn ch

n chế

ếđố

đối v

i vớ

ới h

i hướ

ướng c

ng củ

ủa vect

a vectơ

ơmoment xung l

moment xung lượ

ượng

ng

đượ

được g

c gọ

ọi l

i là

às

sự

ựl

lượ

ượng t

ng tử

ửho

hoá

ákh

khô

ông gian

ng gian.

.

11

12

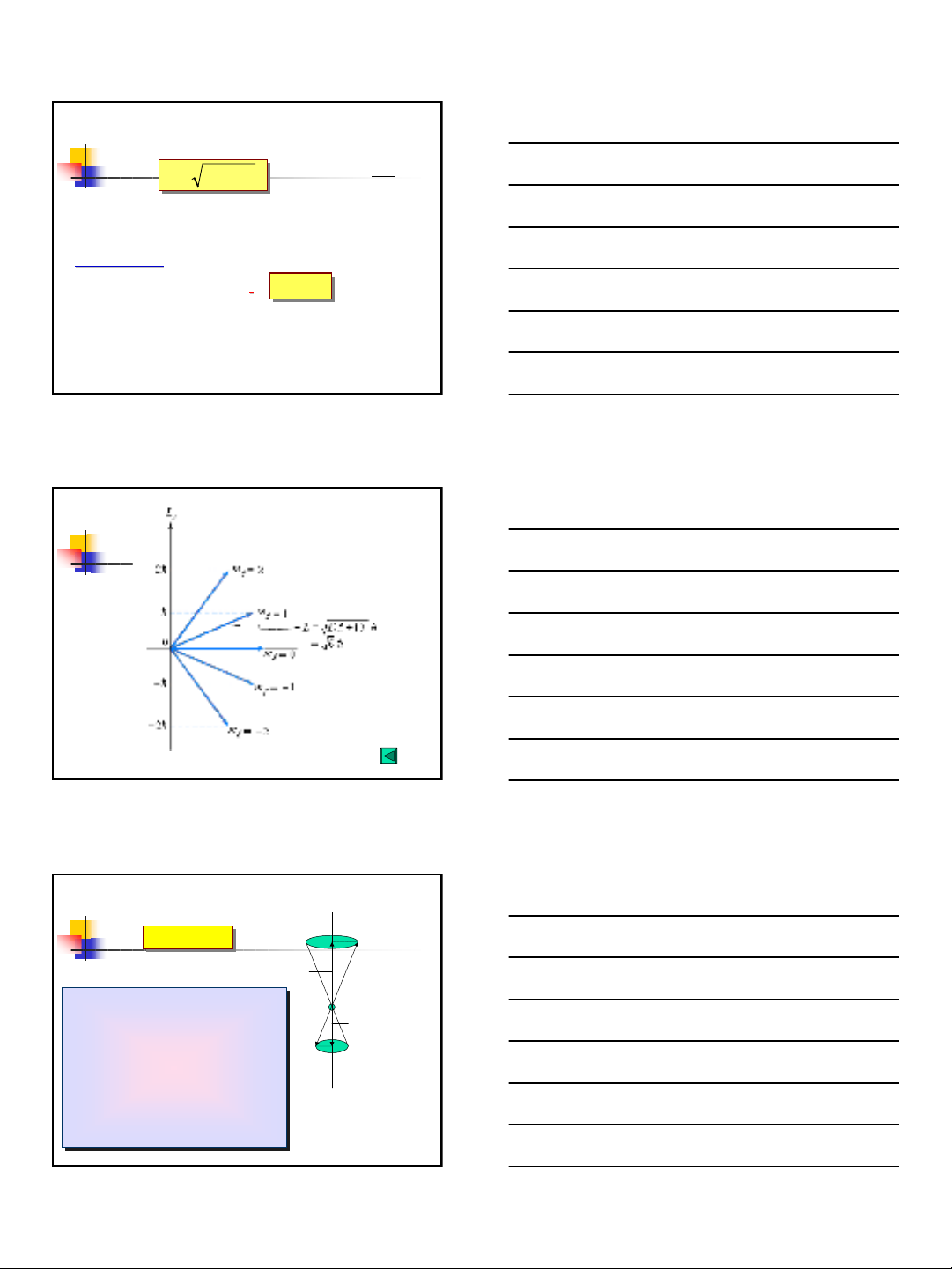
Mét m« h×nh vect¬ h÷u Ých

hL ≅∆∆

θ

.

L

z

µ

h

l

mLz=

Bz m

µµ

.

,ll −=

Một khi chúng ta xác định được số

lượng tửtừ, có nghĩa là Lzđược biết

chính xác; tức là = 0. Phương trình trên

khi đóyêu cầu rằng

∆θ

cần phải lớn vô

hạn, tức là chúng ta hoàn toàn không có

thông tin gì vềvịtrí góc của vectơ

moment xung lượng chuyển động tuếsai

chung quang trục z. Chúng ta chỉbiết

được độ lớn của Lvà hình chiếu Lz của

nó trên trục z.

Một khi chúng ta xác định được số

lượng tửtừ, có nghĩa là Lzđược biết

chính xác; tức là = 0. Phương trình trên

khi đóyêu cầu rằng

∆θ

cần phải lớn vô

hạn, tức là chúng ta hoàn toàn không có

thông tin gì vềvịtrí góc của vectơ

moment xung lượng chuyển động tuếsai

chung quang trục z. Chúng ta chỉbiết

được độ lớn của Lvà hình chiếu Lz của

nó trên trục z.

5

13

Moment tõ quü ®¹o

ll

hmm

m

e

Bz

µµ

−=−= 2

Magnetôn Bohr :

m

eh

B

π

µ

4

== 9,274 . 10-24 J /T =5,788 . 10-5 eV /T

L

r

h

rB

µ

−=

14

3.5

3.5 Moment spin vµ moment tõ spin

Moment spin vµ moment tõ spin

•Dù có bịnhốt trong nguyên tửhay không, các

điện tửđều có moment xung lượng nội tại của

riêng mình. Đây hoàn toàn là kết quảcủa QM -

được Goldsmith & Uhlenbeck đưa ra dựa trên kết

quảthực nghiệm.

•Người ta gọi nó là moment spin và nó cũng bị

lượng tửhoá không gian với các thành phần khảdĩ

theo phương zđược cho bởi

•Dù có bịnhốt trong nguyên tửhay không, các

điện tửđều có moment xung lượng nội tại của

riêng mình. Đây hoàn toàn là kết quảcủa QM -

được Goldsmith & Uhlenbeck đưa ra dựa trên kết

quảthực nghiệm.

•Người ta gọi nó là moment spin và nó cũng bị

lượng tửhoá không gian với các thành phần khảdĩ

theo phương zđược cho bởi

h.

zz mS =

sốlượng tửspin mz= +1/2 và –1/2

15

C

Cá

ác s

c số

ốl

lượ

ượng t

ng tử

ửc

củ

ủa nguy

a nguyê

ên t

n tử

ửhi

hiđ

đr

rô

ô

∞

n

(2 +1)

2

Năng lượng

Moment quỹđạo

Moment spin

1, 2, 3 ….

0, 1, 2 …(n-1)

0, ±1, ±2,.. . .±

±1/2

nSốlượng tửchính

Sốlượng tửquỹđạo

Sốlượng tửtừ

Sốlượng tửspin

Sốcác giá

trịkhảdĩ

Liên quan với

Các giá trịcho

phép

Ký hiệuTên

s

m

l

m

l

ll

Vật lý hiện đại (modern physics) - Chương 3

Chủ đề:

Tài liệu liên quan

Tài liêu mới

AI tóm tắt

Giới thiệu tài liệu

Đối tượng sử dụng

Từ khoá chính

Nội dung tóm tắt

Hỗ trợ

Phương thức thanh toán

Theo dõi chúng tôi