1
X©y dùng hÖ thÝ nghiÖm §iÒu khiÓn R« bèt
víi qu¸ tr×nh nhËn d¹ng vËt thÓ ®éng
trªn c¬ së Camera
TS Lª B¸ Dòng
Ths Hµ M¹nh §µo
KS NguyÔn Thanh Tïng
ViÖn CNTT
lbdung@ioit.ncst.ac.vn
Tãm t¾t:
Bµi b¸o tr×nh bÇy qu¸ tr×nh x©y dùng, thiÕt kÕ hÖ thÝ nghiÖm ®iÒu khiÓn R« bèt víi qu¸ tr×nh nhËn d¹ng
vËt thÓ ®éng trªn c¬ së Camera. Víi qu¸ tr×nh nhËn d¹ng ®éng c¸c vÞ trÝ vµ h−íng cña vËt thÓ th«ng qua ¶nh
vËt thÓ tõ thêi ®iÓm c¾t mÉu, mét thuËt to¸n −íc l−îc vÞ trÝ ®−îc x©y dùng. Víi c¸c vÞ trÝ ®· −íc l−îng, thuËt
to¸n ®iÒu khiÓn ®−îc thiÕt kÕ ®Ó ®−a ®Çu tay n¾m ®Õn vÞ trÝ ®· ®−îc −íc l−îng vµ di chuyÓn vËt thÓ ®Õn
mét vÞ trÝ x¸c ®Þnh trong kh«ng gian lµm viÖc vµ kh«ng gian quan s¸t ®−îc cña Camera.
Abstract:
The paper presents a process to create a robot control system with dynamic recognition of image
object based on Camera. With the position and orientation of object is determined on the sampling time via
image recognition, an estimation algorithm is created. By the position and orientation are determined, an
robot control algorithm is constructed to move the end effectors to estimated position and orientation of the
object and take the object to other position and orientation on the working space and camera space.
1. Më ®Çu
§iÒu khiÓn Robot trªn c¬ së Camera ®−îc thiÕt kÕ theo 1 sè yªu cÇu c¬ b¶n nh− sau vÒ
mÆt kÜ thuËt:
- Camera ®−îc ®Æt cè ®Þnh trong kh«ng gian lµm viÖc cña Robot
- Camera ®−îc treo t¹i ®Çu tay n¾m end- effector cña Robot.
Trong bµi b¸o nµy c¸c t¸c gi¶ ®Ò cËp ®Õn m« h×nh thÝ nghiÖm nhËn d¹ng vËt thÓ ®éng vµ
®iÒu khiÓn R«bèt víi Camera ®Æt cè ®Þnh trong kh«ng gian lµm viÖc cña R« bèt
2. M« h×nh ®iÒu khiÓn Robot víi víi Camera ®Æt cè ®Þnh trong
kh«ng gian lµm viÖc cña R« bèt
M« h×nh ®iÒu khiÓn Robot víi Camera ®Æt cè ®Þnh trong kh«ng gian lµm viÖc cña R«
bèt cho phÐp ta thùc hiÖn hÖ ®iÒu khiÓn kÝn víi qu¸ tr×nh quan s¸t (®o vÞ trÝ vµ h−íng cña vËt
thÓ th«ng qua thiÕt bÞ ®o quang). ë ®©y c¸c tÝn hiÖu ®o ®−îc thùc hiÖn qua ®Çu ®o (visual
sensor ) vµ ®−îc ®Æt trong hÖ kÝn víi viÖc nhËn d¹ng vËt thÓ trong thêi gian thùc. M« h×nh ®iÒu
khiÓn víi c¸c phÐp ®o nh×n trong m¹ch ph¶n håi kÝn ®−îc gäi lµ hÖ visual sensor system. Víi
hÖ visual sensor system ®−îc ph©n ra hai nhãm:
. §iÒu khiÓn Robot trªn c¬ së camera th«ng qua viÖc x¸c lËp vÞ trÝ cña vËt thÓ [1], [2],
[3]
. §iÒu khiÓn Robot víi camera nh»m x¸c lËp c¸c tÝnh chÊt cña vËt thÓ [1], [2],[3]
2
3. Bµi to¸n ®iÒu khiÓn Robot víi qu¸ tr×nh nhËn d¹ng ®éng
3.1 Dù b¸o vÒ vÞ trÝ vµ h−íng cña vËt thÓ
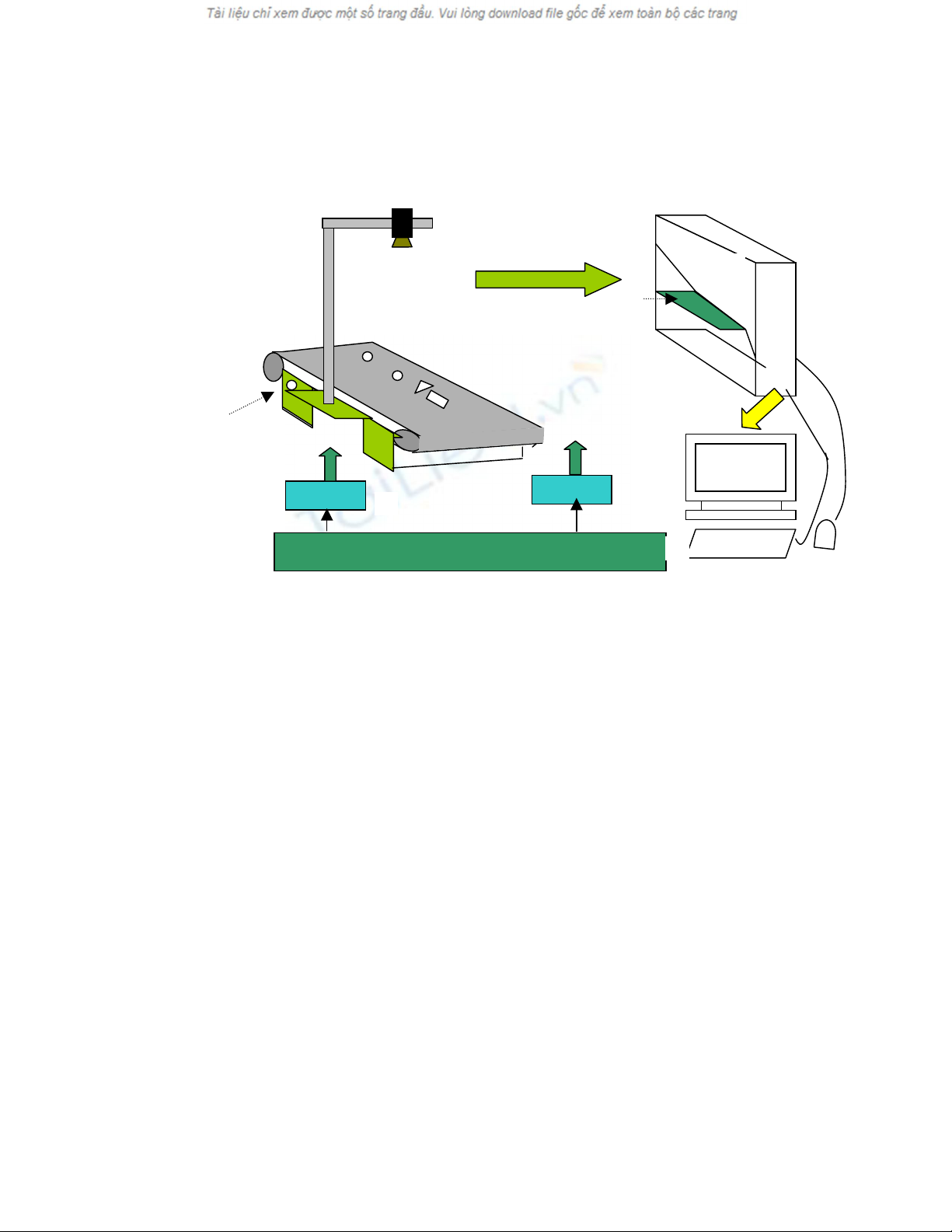
H×nh 1 S¬ ®å hÖ thÝ nghiÖm
C¸c th«ng tin tõ c¸c ®Çu ®o ®−îc chÝnh x¸c ho¸ th«ng qua c¸c phÐp nhËn d¹ng. C¸c vËt
thÓ chuyÓn ®éng ®−îc x¸c ®Þnh b»ng c¸c ph−¬ng ph¸p ¶nh tr«i (optic flow method), ë ®©y
kh«ng xÐt cô thÓ c¸c ®iÓm ¶nh mµ vÞ trÝ vµ tèc ®é ¶nh coi nh− lµ c¸c gi¸ trÞ gi¸n tiÕp. NÕu vÞ trÝ
cña vËt thÓ chuyÓn ®éng ®−îc x¸c ®Þnh tõ ¶nh, th× gi¸ trÞ vÞ trÝ ®ã khi tÝnh to¸n ®· lµ gi¸ trÞ cò
cña mét vµi thêi ®iÓm c¾t mÉu tr−íc ®ã. Do ®ã ®Ó cã thÓ cã ®−îc gi¸ trÞ tÝnh to¸n vÞ trÝ vµ tèc
®é mét c¸ch chÝnh x¸c, hay ta cßn gäi lµ vÞ trÝ vµ tèc ®é cña vËt thÓ t−¬ng ®èi víi camera, trong
tr−êng hîp nµy chóng ta cÇn ph¶i x©y dùng mét m« h×nh dù b¸o. Th«ng sè dù b¸o ®−îc x¸c
®Þnh th«ng qua chuyÓn ®éng cña vËt thÓ. Tõ ®ã cã thÓ thiÕt kÕ ®−îc quü ®¹o theo thêi gian thùc
tÕ cña chuyÓn ®éng Robot vµ thiÕt kÕ thuËt ®iÒu khiÓn
Gi¶ sö vËt thÓ víi vÞ trÝ vµ tèc ®é ®−îc x¸c ®Þnh liªn tôc. NÕu ë thêi ®iÓm kTV cã vÞ trÝ lµ
P0(kTV) vµ h−íng cña vËt thÓ lµ
Φ
0(kTV), nh− vËy chuyÓn ®éng cña vËt thÓ trong qu¸ tr×nh nh×n
thÊy qua c¸c thêi ®iÓm kTV (k = 1 ...) ®−îc x¸c ®Þnh
W0(kTV)= [P0
x(kTv), P0
y(kTv), P0
z(kTv),
Φ
0
x(kTv),
Φ
0
y(kTv),
Φ
0
z(kTv)]T (1)
Víi TV thêi gian quan s¸t
x,y,z lµ to¹ ®é §Ò C¸c cña hÖ
T.... miªu t¶ chuyÓn vÞ
ë ®©y cã thÓ hiÓu lµ:
Vector vÞ trÝ bao gåm vÞ trÝ vµ h−íng cña Robot
PhÇn mÒm
Nguån ®iÖn
Ada
p
te
K
e
y
boar
d
1
2
4
5
6
9
1
11
1
1
11
Ada
p
te
3
Vector tèc ®é bao gåm phÐp quay vµ phÐp tÞnh tiÕn
Tõ viÖc x¸c ®Þnh vÞ trÝ vËt thÓ qua ¶nh. C¸c gi¸ trÞ ®o ®−îc sö dông cho viÖc ®iÒu khiÓn
lµ vÞ trÝ ®−îc −íc l−îng ë thêi ®iÓm Tv + mTc th«ng qua c¸c th«ng tin ë thêi ®iÓm (k -1)Tv víi
Tc lµ chu kú c¾t mÉu cña vßng ®iÒu khiÓn (Tv >Tc) vµ m = 1....T/Tv lµ sè nguyªn
Tèc ®é chuyÓn ®éng vËt thÓ ®−îc tÝnh to¸n qua vÞ trÝ t©m ®iÓm cña vËt thÓ ®−îc x¸c
®Þnh ë thêi ®iÓm hiÖn t¹i vµ thêi ®iÓm tr−íc ®ã. Gäi v0(kTv) lµ vËn tèc cña vËt thÓ ë thêi ®iÓm k
Tc ®−îc x¸c ®Þnh b»ng
v
0(kTv) = {W0(kTv) - W0[(k-1)Tv]}/Tv (2)
Víi v0(kTv) tèc ®é ë thêi ®iÓm kTv cã thÓ viÕt d−íi d¹ng sau
v0(kTv) = [v0
x(kTv) v0
y(kTv) v0
z(kTv), ω0
x(kTv) ω 0
y(kTv) ω 0
z(kTv) ]T
3 thµnh phÇn ®Çu lµ tèc ®é chuyÓn ®éng th¼ng.
3 thµnh phÇn sau lµ tèc ®é chuyÓn ®éng quay.
Víi qu¸ tr×nh chuyÓn ®éng cña vËt thÓ, tèc ®é trong (2) ®−îc x¸c ®Þnh th«ng qua m«
h×nh AR vµ m« h×nh AR ®−îc chän nh− sau theo [9]:
)()()()( 0010
vvv
okTekTvzAkTv += − (3)
vector eo(kTv) lµ sai sè m« h×nh vµ ma trËn Ao(z-1) ®−îc ®Þnh nghÜa
n
n
ozAzAzAzA −−−− +++= 020
2
10
1
1...)( (4)
Ma trËn vu«ng A0
i , i=1,2,...,n chøa c¸c gi¸ trÞ ch−a biÕt, z-1 lµ to¸n tö trÔ liªn quan ®Õn
chu kú cÊt mÉu quan s¸t vµ z-1v0(kTi)=v0[(k-1)T] ; n- sè nguyªn lµ ®é lín cña Ma trËn
víi i=1,2,...,6
T- chu kú c¾t mÉu
§Ó −íc l−îng c¸c th«ng sè ch−a biÕt cña (3) ta sö dông ph−¬ng ph¸p trong [5]
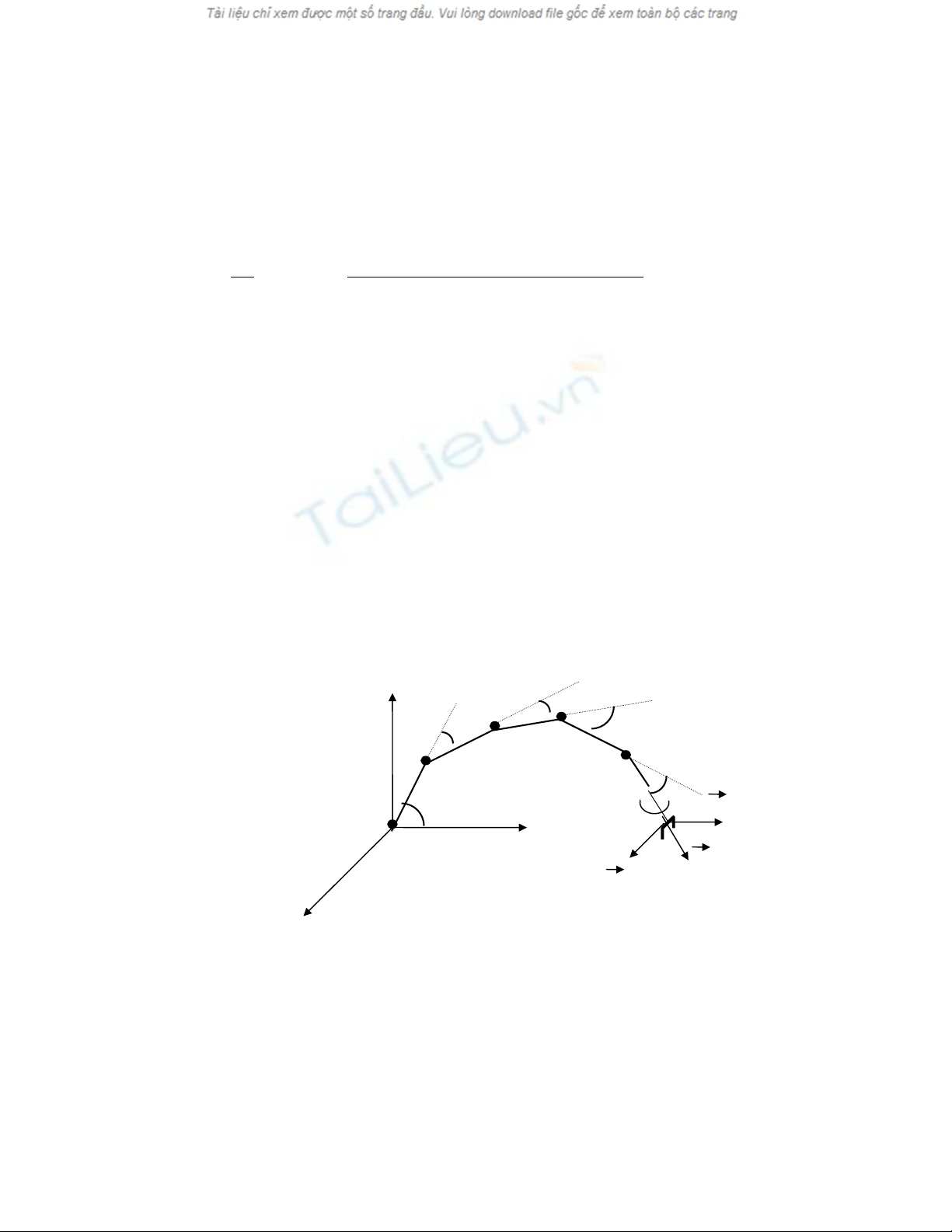
(k-1)TV kTV (k+1)TV
kTV+TC kTV+2TC
H
×nh 2 Qu¸ tr×nh c¾t mÉu
[
]
[][]
[]
T
n
i
n
iiii
T
n
T
TTT
aaaa
AAA
nkvkvkvkM
0
6
0
1
10
6
10
1
0
0
6
0
2
0
1
00
2
0
1
0
0000
.........
......
))(.....())2(())1(()1(
=
==
−−−=−
α
αααα
(5)
(6
(7)
4
)()1()()( 0000 kekMkv T+−=
α
(8)
víi ph−¬ng ph¸p b×nh ph−¬ng tèi thiÓu, −íc l−îng gi¸ trÞ vector
α
0 trong [5]
[]
[]
10
)9(
)1()1()1(
)1()1()1()1(
)1(
1
)(
))1()1(
0
)()(1(*)()1(
0
)(
0
0
0000
0000
0
0
0
0000
≤<
−−−+
−−−−
−−=
−
−−−+−=
∧∧
∧
µ
µ
µ
αα
α
kMkPkM
kPkMkMkP
kPkP
kMk
i
kvkMkPk
i
k
j
T
T
T
i
VÞ trÝ vËt thÓ cã thÓ viÕt tõ (2)
[ ][][]
)10()1/()1/()1/( 000
CVVVVVC mTTkkTvTkkTWTkmTkTW −+−=−+ ∧∧∧
3.2 ThiÕt kÕ bé ®iÒu khiÓn:
3.2.1 Mét sè vÊn ®Ò c¬ b¶n cña ®éng häc vÞ trÝ
Mét vËt thÓ trong kh«ng gian th−êng ®−îc m« t¶ b»ng s¸u tham sè sau nh− [8]:
- 3 tham sè vÒ vÞ trÝ (position): x, y, z hoÆc px, py, pz, nh− biÓu diÔn ë (1)
- 3 tham sè vÒ h−íng (orientation):
φ
x ,
φ
y ,
φ
z.
XÐt robot trong hÖ to¹ ®é §Òc¸c víi lo¹i robot nèi khíp (chØ cã khíp quay mµ kh«ng cã
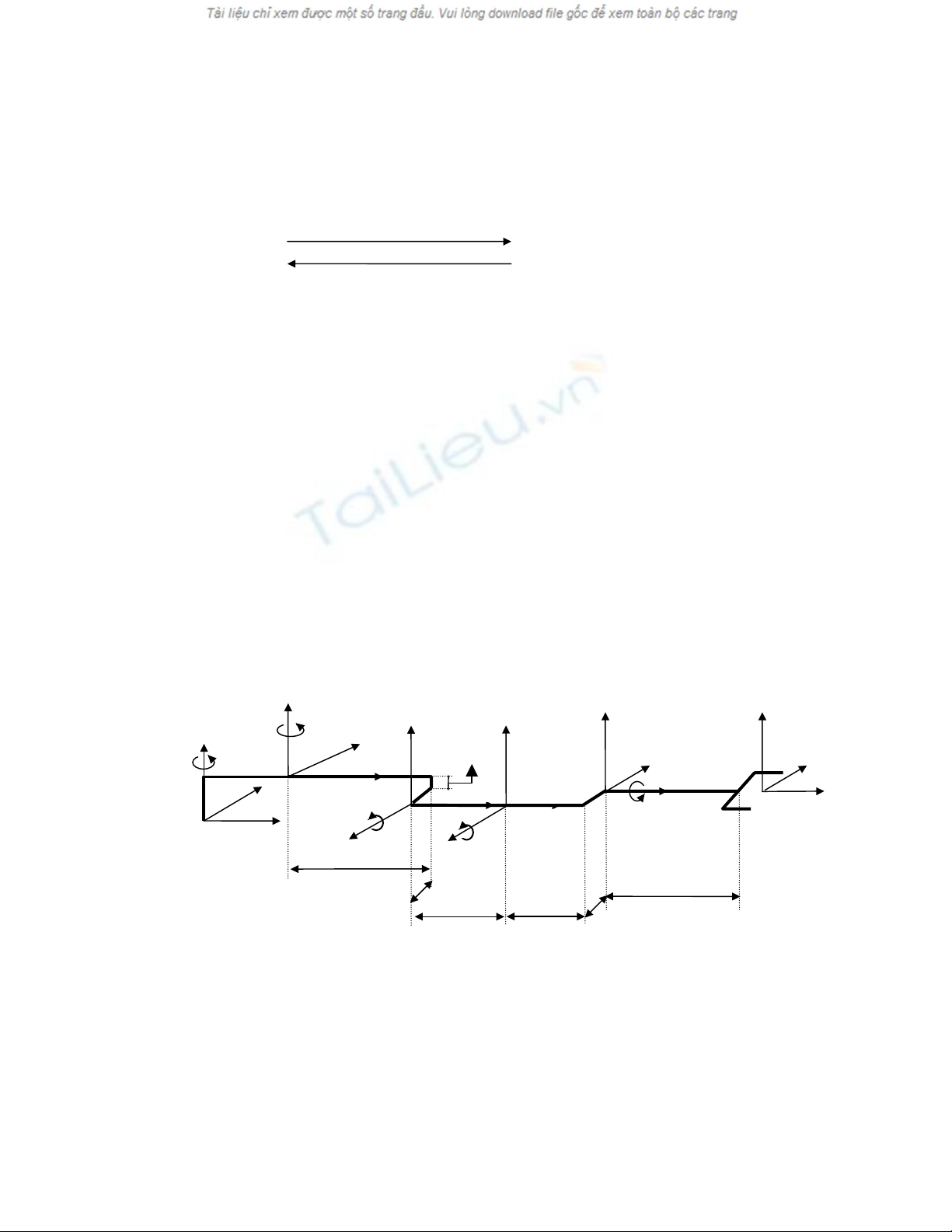
khíp tÞnh tiÕn) víi gi¶ thiÕt robot co 6 khíp quay
H×nh 3 R«bèt chØ cã kíp quay
C¸c biÕn trong
θ
1 ,
θ
2 ,
θ
3 ,
θ
4 ,
θ
5 ,
θ
6 lµ c¸c gãc chuyÓn ®éng t−¬ng ®èi cña c¸c khíp (so
víi vÞ trÝ cò).
C¸c biÕn ngoµi x, y, z,
φ
x ,
φ
y ,
φ
z lµ vÞ trÝ h×nh häc cña tay n¾m robot.
- x, y, z lµ to¹ ®é cña tay n¾m robot.
-
φ
x ,
φ
y ,
φ
z lµ c¸c gãc quay cña tay n¾m robot quanh c¸c trôc x, y, z.
x
y
z
θ6
θ5
θ4
θ
3
θ2
θ1
n
o
a
5
Sù biÕn ®æi qua l¹i gi÷a c¸c biÕn ngoµi vµ biÕn trong thÓ hiÖn nh− sau:
θ
=
θ
θ
θ
θ
θ
θ
1
2
3
4
5
6
x
y
z
x
y
z
φ
φ
φ
VÊn ®Ò c¬ b¶n cña bµi to¸n g¾p vËt trªn sµn lµ tõ vÞ trÝ (x, y, z,
φ
x ,
φ
y ,
φ
z) x¸c ®Þnh cña vËt, ta
ph¶i tÝnh to¸n ®éng häc ng−îc ®Ó x¸c ®Þnh c¸c gãc quay (
θ
1 ,
θ
2 ,
θ
3 ,
θ
4 ,
θ
5 ,
θ
6) cña c¸c khíp
vµ ®iÒu khiÓn c¸c khíp quay cña robot theo c¸c gãc ®· tÝnh to¸n ®Ó di chuyÓn tay n¾m robot
®Õn ®óng vÞ trÝ vµ h−íng cña vËt. ViÖc tÝnh to¸n bé th«ng sè c¸c gãc quay (
θ
1 ,
θ
2 ,
θ
3 ,
θ
4 ,
θ
5 ,
θ
6) cña c¸c khíp tuú thuéc vµo hÖ ph−¬ng tr×nh ®éng häc ng−îc ®· x©y dùng cã tèi −u hay
kh«ng. NhiÒu khi ph¶i gi¶i hÖ ph−¬ng tr×nh siªu viÖt trong bµi to¸n ng−îc víi thêi gian rÊt l©u,
®«i khi lêi gi¶i kh«ng ®¹t sù héi tô. §iÒu nµy kh«ng ®¶m b¶o thêi gian thùc trong ®iÒu khiÓn
tay m¸y. Do ®ã viÖc gi¶i bµi to¸n ®éng häc ng−îc ®−a ra ®−îc hÖ ph−¬ng tr×nh tèi −u cã ý
nghÜa võa khoa häc võa thùc tiÔn. Khi ¸p dông vµo thùc tiÔn th× tuú theo tõng lo¹i robot mµ ta
cã thÓ x©y dùng ®−îc hÖ ph−¬ng tr×nh ®éng häc ng−îc theo cÊu tróc hÖ thèng cña nã.
3.2.2 Mét ph−¬ng ph¸p tÝnh to¸n ®éng häc ng−îc cho robot 5 bËc tù do cña hÖ
1. CÊu tróc hÖ thèng cña robot 5 bËc tù do
H×nh 4 CÊu tróc R«Bèt 5 bËc tù do
2. §éng häc thuËn robot 5 bËc tù do theo [8]
Ma trËn biÕn ®æi ®ång nhÊt cña tay n¾m robot nh×n trong hÖ to¹ ®é gèc R
§én
häc n
−îc
§én
g
häc thuËn
z0
θ
2
O
1
y0
z
x0
O
y
1
θ
3
z2
y
2
x
2
O2
x
1
θ
1
z3
y
3
x3
O3
θ
θ
z
4
y
4
x
4
O4
on
a
O
hand
170 mm
93 mm
75 mm
28 mm
10 mm
38 mm 70 mm
10 mm
55 mm
R
H