C2 CAD-CAM> CO SO MHHHH 1 GVC NGUYỄN THẾ TRANH
Chương 2
CƠ SỞ CỦA MÔ HÌNH HOÁ HÌNH HỌC
Trong chương này trình bày tóm tắt các kết quả cơ bản của hình học vi phân và
phép biến đổi toạ độ sử dụng trong mô hình hoá hình học.
2.1 HÌNH HỌC ĐƯỜNG CONG.
Về mặt trực quan, đường cong được định nghĩa như là quĩ đạo điểm thoả mãn
một số điều kiện.
2.1.1 Biểu diễn đường cong.
Về toán học, đường cong có thể dược biểu diễn dưới các dạng:
- Phương trình ẩn.
- Phương trình tường minh.
- Phương trình tham số.
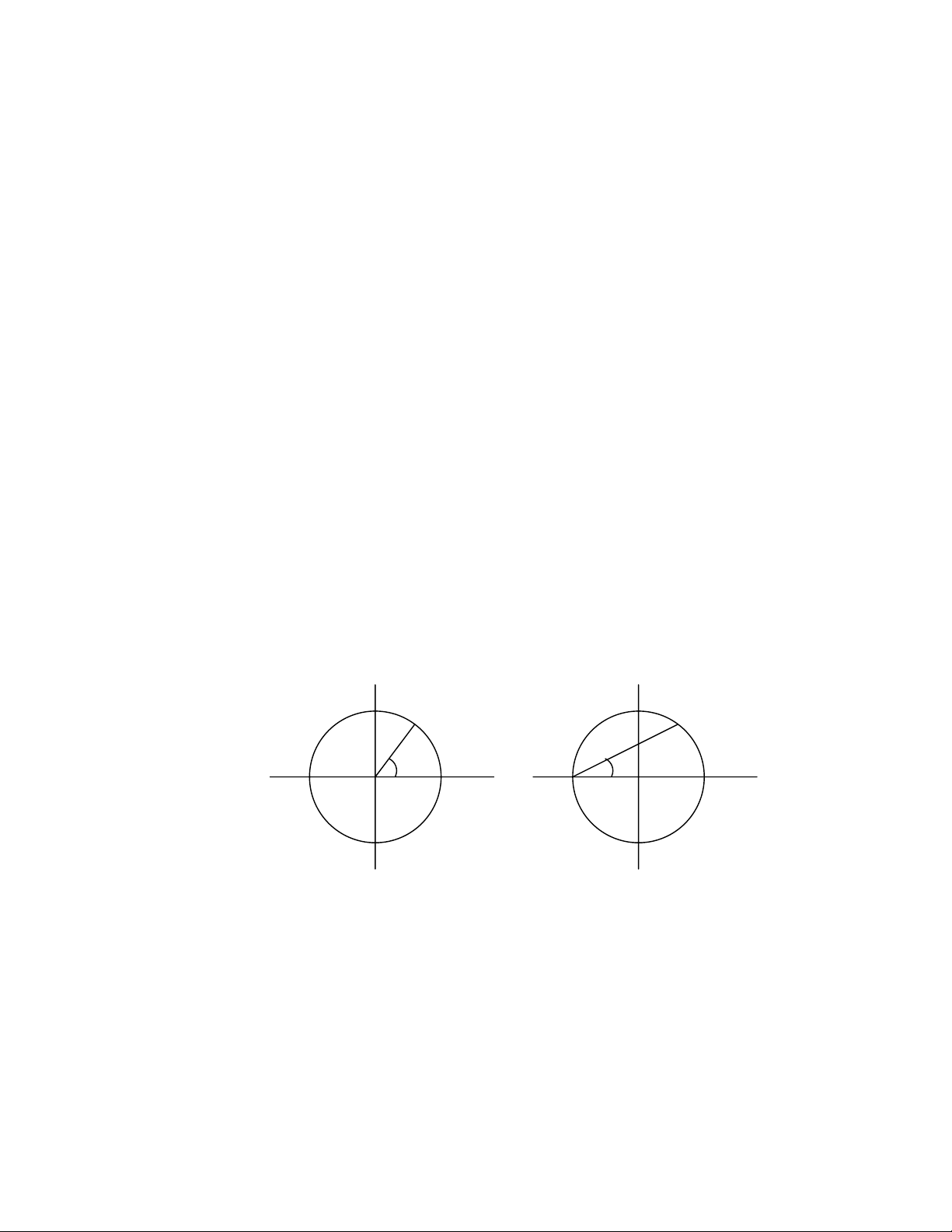
Xét đường tròn đơn vị trên mặt phẳng (x - y), có tâm trùng với gốc hệ toạ độ
trên hình 2.1. Mối quan hệ giữa các toạ độ x và y được mô tả bởi phương trình:
01),( 22 =−+= yxyxf : Phương trình ẩn (2.1)
Nếu chỉ xét phần nửa trên của đường tròn, phương trình biểu diễn là:
2/1
)1()( xxgy −== : Phương trình tường minh (2.2)
Nếu đặt góc θ giữa đoạn thẳng PO và trục x là tham số của đường tròn, ta có:
θ
θ
cos)( == xx ;
θ
θ
sin)(
=
=
yy : Phương trình tham số (2.3)
Trường hợp đặt góc α tạo bởi PQ và trục x là tham số, thì )1/(
+
== xytgt
α
Kết hợp với phương trình (2.1) ta có:
)1/()1()( 22 tttxx +−== ; )1/(2)( 2
tttyy +== (2.4)
Đây cũng là phương trình tham số của đường tròn và được gọi là phương trình
tham số đa thức hữu tỷ. Quá trình thiết lập phương trình tham số hữu tỷ của đường
cong và mặt cong từ phương trình đa thức ẩn được gọi là tham số hoá.
Nên biểu diễn đường cong 3D thích hợp dưới dạng phương trình tham số:
)(txx =; )(tyy
=
; )(tzz
=
hay dưới dạng vectơ: )](),(),([)( tztytxtr
=
y
x
y
P(x,y)
o
θ
o
y
x
y
P(x,y)
o
Q
Hình 2.1 : Tham số hoá đường tròn đơn vị
C2 CAD-CAM> CO SO MHHHH 2 GVC NGUYỄN THẾ TRANH
Theo dạng phương trình tham số, đường cong được định nghĩa một cách dễ
dàng bằng cách xác định miền giới hạn của tham số. Không thể xác định đường cong
3D bởi phương trình ẩn hay tường minh, bởi vì phương trình ẩn g(x,y,z)=0 biểu diễn
mặt cong, do đó cần hai phương trình để xác định đường cong 3D. Trong trường hợp
này, đường cong được định nghĩa như giao tuyến giữa hai mặt cong.
2.1.2 Đặc tính của đường cong.
Trong phần này để biểu diễn đường cong, ta sử dụng phương trình tham số
chuẩn tắc: )](),(),([)( tztytxtrr
=
=
Đặc tính cơ bản của đường cong, bao gồm:
a. Độ chảy của đường cong.
b. Vectơ tiếp tuyến đơn vị.
c. Vectơ pháp tuyến chính.
d. Độ cong và bán kính cong.
1. Độ chảy:
Độ lớn của vectơ đạo hàm )(tr
& được gọi là độ chảy của đường cong:
)()( trts && = (2.5)
Hãy tưởng tượng đường cong là con đường và tham số t tượng trưng cho thời
gian. Như vậy, độ chảy của đường cong tương ứng với tốc độ chạy xe. Đại lượng này
được sử dụng trong thuật toán nội suy hình học theo phương pháp quét hình.
Nếu đặt quãng đường đi được là tham số s, phương trình đường cong dạng r(s)
trở thành phương trình tham số tự nhiên với độ chảy bằng 1. Độ chảy của đường cong
không phải là đặc tính riêng của đường cong, đó là kết quả của phép tham số hoá.
2. Vectơ tiếp tuyến đơn vị:
Cho s là tham số tự nhiên của đường cong r(t), sao cho:
dttrs ∫
=
θ
0
)(
&
Vectơ tiếp tuyến đơn vị của đường cong r(t) được định nghĩa như sau:
dsdrT /= (2.6)
hay dưới dạng vi phân: )(/)( trtrT &&
= (2.7)
3. Vectơ pháp tuyến chính:
Lấy đạo hàm vectơ tiếp tuyến đơn vị T theo t và chuẩn hoá giá trị, chúng ta có
vectơ đơn vị N, được gọi là vectơ pháp tuyến chính của đường cong:
dsdTdsdTdtdtdtdTN //)/(//)/( ≡= (2.8)
Vì T là vectơ đơn vị (T.T=1), do đó
vectơ N vuông góc với vectơ T (Hình 2.2).
Mặt phẳng định nghĩa bởi vectơ T
và N được gọi là mặt phẳng mật tiếp. Vectơ
B vuông góc với vectơ N và T được gọi là
vectơ pháp tuyến đôi xác định bởi quan hệ:
B = TxN
T
N
Đườn
g
t
r
òn
m
ậ
t ti
ếp
Hình 2.2 : Vectơ pháp tuyến chính
và đường tròn mật tiếp
C2 CAD-CAM> CO SO MHHHH 3 GVC NGUYỄN THẾ TRANH
4. Độ cong và bán kính cong:
Hãy cho s là tham số tự hiên và T là vectơ tiếp tuyến đơn vị của đường cong
r(t). Độ cong được định nghĩa như sau:
dsdTk /= (2.9)
hay dưới dạng vi phân:
3
r
rr
k
&
&&& ×
= (2.10)
trong đó: dtrdrdttdrr /;/)( &&&& ≡≡ . Đối với đường cong 2D dạng phương trình tường
minh y = y(x), phương trình trên có dạng:
2/32 )1/( yyk &&& +=
trong đó: dxdyy /≡
& ; dxydy /
&&&
≡
Hãy xét đường tròn trên mặt phẳng mật tiếp (Hình 2.2), đi qua điểm hiện thời
r(t) và độ cong của nó bằng chính độ cong của đường cong tại điểm này. Đường tròn
này được gọi là đường tròn mật tiếp, bán kính của đường tròn mật tiếp được gọi là bán
kính cong và được xác định bởi:
k/1
=
ρ
(2.11)
5. Độ xoắn của đường cong:
Độ xoắn của đường cong 3D được định nghĩa như sau:
NdsdB )./(−=
τ
trong đó N là vectơ pháp tuyến chính; B là vectơ pháp tuyến đôi. Phương trình cơ bản
mô tả đặc tính của đường cong 3D được gọi là phương trình Serret-Frenet:
;/ Tdsdr = kNdsdT
=
/
kTBdsdN
−
=
τ
/; 1
/−
−= NdsdB
τ
(2.12)
2.2 HÌNH HỌC MẶT CONG.
2.2.1 Phương pháp biểu diễn mặt cong:
1. Mô hình mặt cong cong dạng phương trình ẩn.
Hãy xét mặt cầu đơn vị với tâm tại gốc toạ độ Đề các. Các điểm phía trong mặt
cầu thoả bất đẳng thức: 01
222 <−++ zyx
và phương trình: 01
222 =−++ zyx (2.13)
biểu diễn các điểm thuộc mặt cầu.
Xét một cách tổng quát, phương trình ẩn g(x,y,z) = 0 biểu diễn mặt cong giới
hạn bởi hai nửa không gian g(x,y,z) > 0 và g(x,y,z) < 0.
2. Mô hình mặt cong dạng phương trình tham số.
Theo hình học vi phân, mặt cong được định nghĩa như là ảnh của phép ánh xạ
chính qui tập hợp điểm trong không gian 2D vào không gian 3D và được biểu diễn bởi
phương trình:
)],(),,(),,([),( vuzvuyvuxvur = (2.14)
trong đó: u và v là tham số của mặt cong.
Đối với hình cầu đơn vị, ta có thể dễ dàng tham số hoá phương trình (2.13)
bằng cách đặt tham số u là vĩ tuyến và tham số v là kinh tuyến của mặt cầu:
)sin,sincos,cos(cos),( vuvuvvur = (2.15)
C2 CAD-CAM> CO SO MHHHH 4 GVC NGUYỄN THẾ TRANH
với:
π
20 ≤
≤
u và 2/2/
π
π
≤
≤
−
v
Tương tự như đường tròn đơn vị có thể tham số hoá phương trình mặt cầu dưới
hình thức khác, bằng cách sử dụng đa thức hữu tỷ.
3. Mô hình mặt cong dạng phương trình phi tham số.
Khi miền xác định của mặt cong là mặt phẳng x-y của hệ toạ độ Descarte
),( yvxu ≡≡ , mô hình tham số (2.14) trở thành phi tham số:
)),(,,(),( vuzvuvur = hay ),( yxzz
=
(2.16)
Nếu chỉ xét bán cầu trên của mặt cầu đơn vị thì phương trình (2.13) được biểu
diễn dưới dạng tường minh:
2/122 )1( yxz −−= với 1)( 22 ≤+ yx (2.17)
2.2.2 Tiếp tuyến và pháp tuyến của mặt cong.
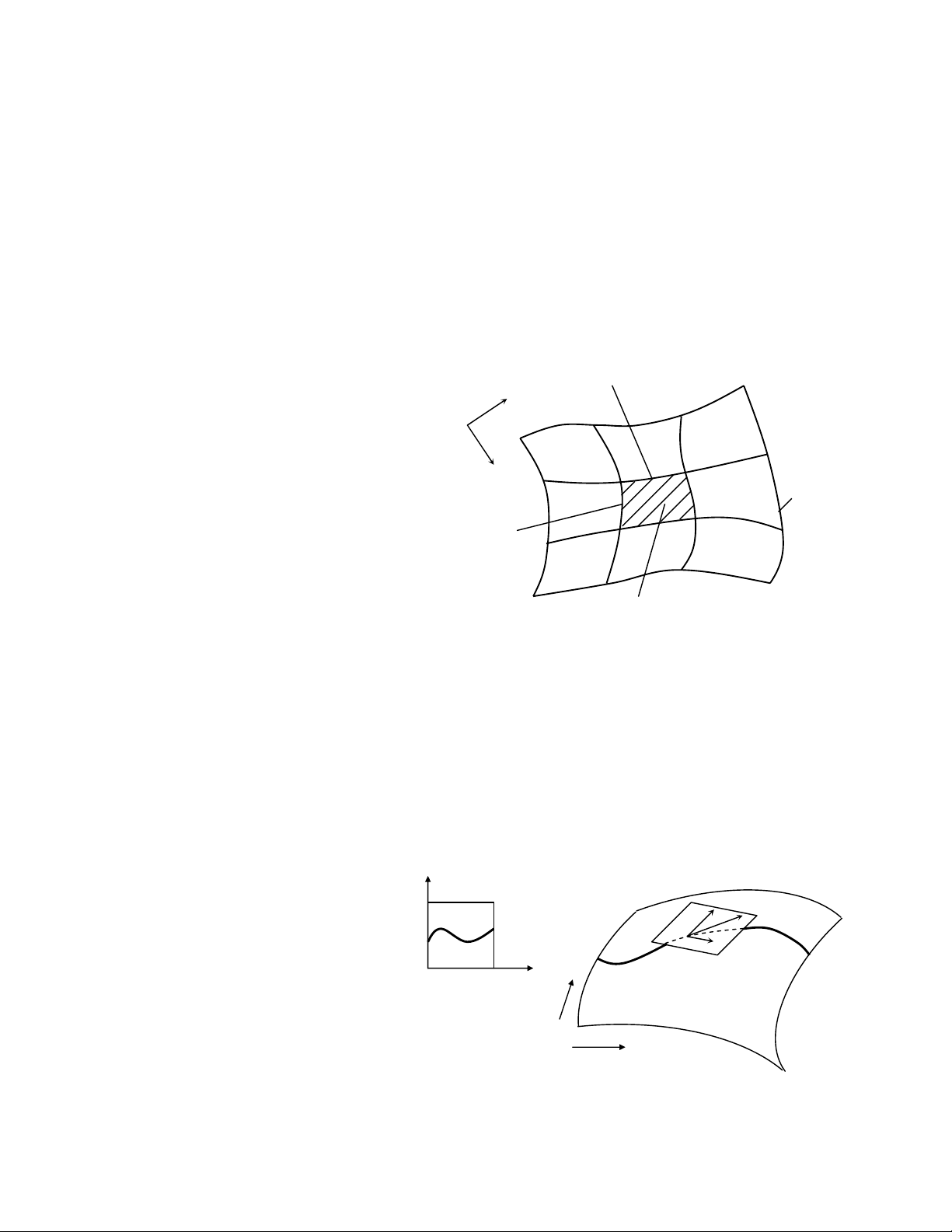
Xét đường cong tham số 2D: q(t) trên miền (u,v) của mặt cong tham số r(u,v)
(Hình 2.4):
T
tvtutq )](),([)( = (2.18)
Hãy cho đường cong r(t) là hình chiếu của đường cong q(t) trên mặt cong
r(u,v), sao cho:
r(t) = r(u(t), v(t))
= (x(u(t), v(t)), y(u(t), v(t)), z(u(t), v(t))) (2.19)
Hình học mặt cong
được minh hoạ trên hình
2.3. Ta thường gọi phần
mặt cong trong miền tham
số giới hạn là mặt lưới. Các
mặt lưới liên kết theo điều
kiện kết nối liên tục tạo
thành mặt cong phức hợp.
u
(u=0,v=0)
v điểm gốc
đường
biên
(u=1,v=1)
đường sinh phương v
đường sinh
phương u
mặt lưới
·
·
·
Hình 2.3 : Hình học mặt cong
q(t)
v
u ru
r(u,v)
r(t)
rv
r
&
u
v
Hình 2.4 - Đường cong trên mặt cong
và mặt phẳng tiếp tuyến
Trường hợp đặc
biệt của (2.19) là đường
cong đẳng tham số:
ttvuu
ttuvv
==
==
)(,
)(,
*
*
C2 CAD-CAM> CO SO MHHHH 5 GVC NGUYỄN THẾ TRANH
Vectơ tiếp tuyến.
Đạo hàm riêng của mặt cong r(u,v) được định nghĩa như sau:
urru∂∂= / ; vrrv
∂
∂= / ; vurruv ∂∂∂= /
2 (2.20)
Lấy đạo hàm phương trình (2.19) theo t, ta có:
vrur
dt
dv
v
r
dt
du
u
r
dt
dr
rvu &&& +=
∂
∂
+
∂
∂
== (2.21)
trong đó:
r
& là vectơ tiếp tuyến của đường cong r(t); ru và rv là vectơ tiếp tuyến của
đường cong đẳng tham số u = u* , v = v*. Ba vectơ tiếp tuyến
r
&, ru, rv xác định mặt
phẳng tiếp tuyến với mặt cong (Hình 2.4).
Vectơ pháp tuyến.
Vectơ pháp tuyến đơn vị n của mặt phẳng tiếp tuyến được gọi là vectơ pháp
tuyến đơn vị của mặt cong tại điểm cho trước và được xác định bởi:
vuvu rrrrn ××= /)( (2.22)
Vectơ pháp tuyến đơn vị rất cần thiết trong các phép khảo sát mặt cong.
Ma trận cơ sở thứ nhất.
Vectơ tiếp tuyến (2.21) có thể được biểu diễn dưới dạng ma trận:
qvrurr vu &&&& Λ=+= (2.23)
trong đó: vu rr ,=Λ ; T
vudtdvdtdudttdqq ][)/,/(/)( &&& === . Giá trị vectơ tiếp tuyến
được tính như sau:
qGqqqrrr TTTT &&&&&&& =ΛΛ== )()(
2 (2.24)
trong đó: ⎥
⎦
⎤
⎢
⎣
⎡
=ΛΛ=
vvvu
vuuu
T
rrrr
rrrr
G..
.. : Ma trận cơ sở thứ nhất. (2.25)
Do đó, vectơ tiếp tuyến đơn vị T được biểu diễn theo G như sau:
2/1
)/()(/ qGqqrrT T&&&&& Λ== (2.26)
Áp dụng ma trận cơ sở thứ nhất, ta có thể tính diện tích mặt cong và diện tích
mặt cắt theo công thức đơn giản sau:
dudvGdudvrrS vu
2/1
∫
∫∫∫ =×= (2.27)
2.2.3 Độ cong.
Ma trận cơ sở thứ hai.
Xét đường cong r(t) trên mặt cong r(u,v) (Hình 2.4). từ (2.21), đạo hàm bậc hai
của r(t) theo t có giá trị như sau:
vuvvvuuvuu rvrurvvrurvruur &&&&&&&&&&&&
+
+
+
+
+
=
)()( (2.28)
Thực hiện phép nhân vô hướng với vectơ pháp tuyến đơn vị n của mặt cong với
chú ý rằng ru.n = rv.n = 0, ta có:
qDqnrvnrvunrunr T
vvuvuu &&&&&&&& =++= .)(.2.)(. 22 (2.29a)
trong đó: ⎥
⎦
⎤
⎢
⎣
⎡
=v
u
q&
&
& ; và ⎥
⎦
⎤
⎢
⎣
⎡
=nrnr
nrnr
D
vvuv
uvuu
..
.. : ma trận cơ sở thứ hai.