III. ĐIỀU KHIỂN LIÊN TỤC
TRONG MIỀN THỜI GIAN
BM Điều Khiển Tự Động
Th.S. Đặng Văn Mỹ
1 Bai 1 - Chuong 3 - DKLT mien t - Mo hinh toan hoc.key - November 12, 2014
III. ĐIỀU KHIỂN LIÊN TỤC TRONG MIỀN THỜI GIAN
3.1 MỘT SỐ CÔNG CỤ TOÁN HỌC
Định nghĩa ma trận
Ma trận hàng, ma trận cột, ma trận đơn vị, ma trận đường chéo
Các phép toán ma trận: cộng, trừ, nhân, chia
Ma trận chuyển vị và các tính chất
Hạng của ma trận
Định thức ma trận
Ma trận nghịch đảo
Với ma trận bù có các ph tử
ĐẠI SỐ MA TRẬN
Amxn
I3x3=
1 0 0
0 1 0
0 0 1
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
Cmxn =Amxn ±Bmxn =(aij +bij )
AB =C⇔cij =aikbkj
k=1
p
∑
AT
(AB)T=ATBT
A(B+C)=AB +AC
A−1=Aadj
det(A)
aij
'=(−1)i+jdet( Aji )
Aadj
my.dangvan@hust.edu.vn
2 Bai 1 - Chuong 3 - DKLT mien t - Mo hinh toan hoc.key - November 12, 2014
III. ĐIỀU KHIỂN LIÊN TỤC TRONG MIỀN THỜI GIAN
3.2 XÂY DỰNG MÔ HÌNH TOÁN HỌC
3.2.1 MÔ HÌNH TRẠNG THÁI
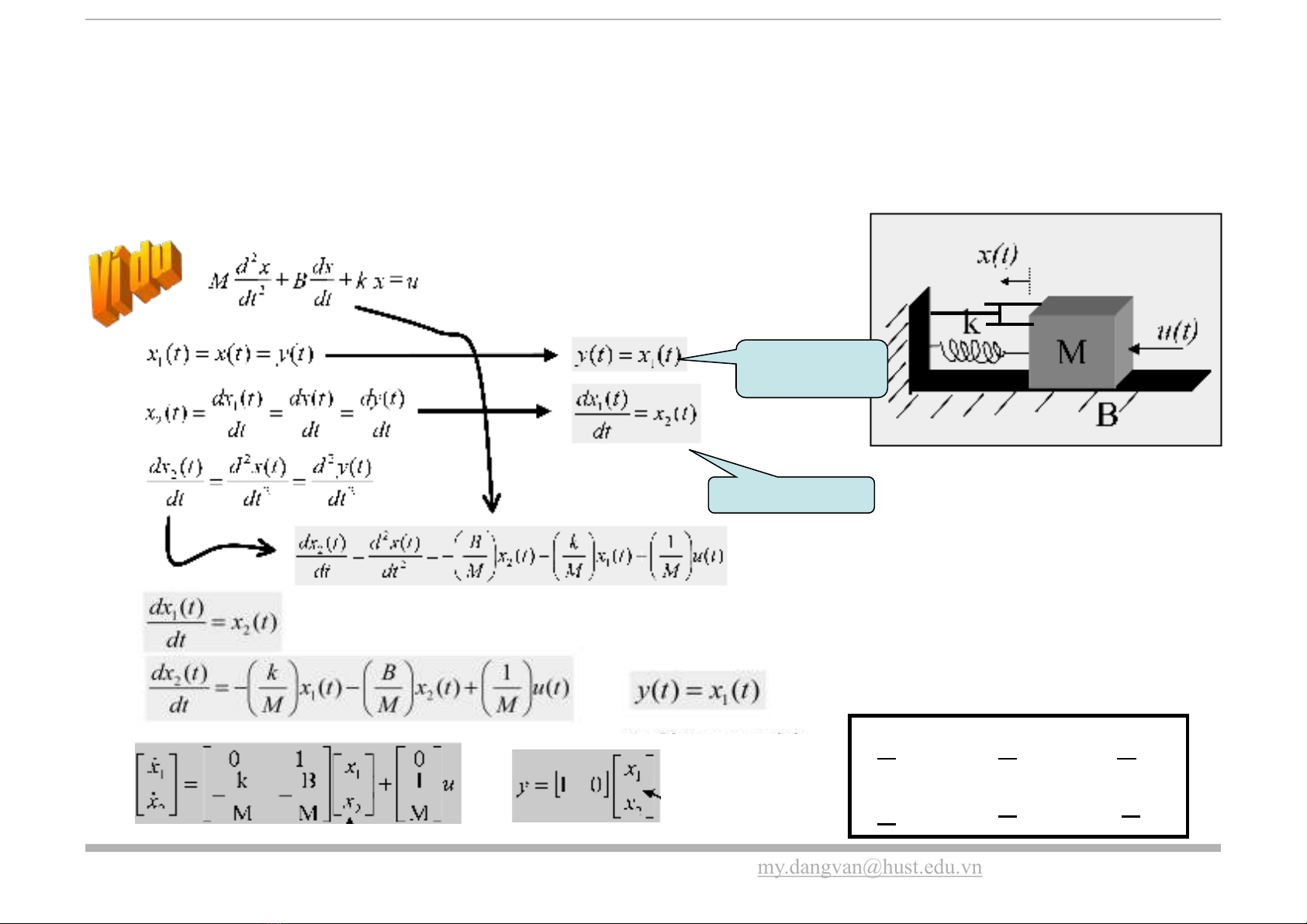
Những hệ thống điều khiển có nhiều đầu vào - nhiều đầu ra (MIMO) thì phương pháp tổng hợp hệ thống trong không
gian trạng thái thường được sử dụng. Phương pháp này cho phép người ta tính được cả các điều kiện khởi tạo để tổng
hợp hệ thống khi cần thiết.
Quãng đường
dịch chuyển
Vận tốc khối vật
&
x(t)=Ax(t)+Bu(t)
y(t)=Cx(t)+Du(t)
⎧
⎨
⎩
B
my.dangvan@hust.edu.vn
3 Bai 1 - Chuong 3 - DKLT mien t - Mo hinh toan hoc.key - November 12, 2014
3.2 XÂY DỰNG MÔ HÌNH TOÁN HỌC
3.2.1 MÔ HÌNH TRẠNG THÁI
Xét hệ gồm có:
m tín hiệu vào
r tín hiệu ra
n biến trạng thái
u(t)={u1(t),...,um(t)}
y(t)={y1(t),..., yr(t)}
x(t)={x1(t),..., xn(t)}
Ưu điểm: So với phương trình hàm truyền, hệ phương trình trạng thái có thể sử dụng
để mô tả hệ MIMO. Ngoài ra, MHTT còn giúp ta khảo sát được trực tiếp các trạng
thái bên trong hệ thống.
&
x(t)=Ax(t)+Bu(t)
y(t)=Cx(t)+Du(t)
⎧
⎨
⎩
A: Ma trận hệ thống (nxn)
B: Ma trận đầu vào (nxm)
C: Ma trận đầu ra (rxn)
D: Ma trận liên thông (rxm)
&
x(t)=A(t)x(t)+B(t)u(t)
y(t)=C(t)x(t)+D(t)u(t)
⎧
⎨
⎩
&
x(t)=A(v)(x(t)+B(v)u(t)
y(t)=C(v)x(t)+D(v)u(t)
⎧
⎨
⎩
Hệ tham số phụ thuộc thời gian Hệ tham số rải (phụ thuộc không gian)
my.dangvan@hust.edu.vn
4 Bai 1 - Chuong 3 - DKLT mien t - Mo hinh toan hoc.key - November 12, 2014
3.2 XÂY DỰNG MÔ HÌNH TOÁN HỌC
3.2.1 MÔ HÌNH TRẠNG THÁI
Xét hệ SISO có một tín hiệu vào u(t) và một tín hiệu ra y(t):
Mô hình được viết lại thành:
Đặt:
XÁC ĐỊNH MÔ HÌNH TRẠNG THÁI TỪ PHƯƠNG
TRÌNH VI PHÂN MÔ TẢ QUAN HỆ VÀO RA
a0y+a1
dy
dt
+... +an−1
dn−1y
dtn−1+dny
dtn=b0u+b1
du
dt
+... +bn−1
dn−1u
dtn−1+bn
dnu
dtn
G(s)=Y(s)
U(s)
=b0+b1s+...+bnsn
a0+a1s+...+an−1sn−1+sn=B(s)
A(s)
X1=U(s)
A(s),X2=sU(s)
A(s),..., Xn=sn−1
U(s)
A(s)
sX1=X2,K,sXn−1=Xn
X1=U(s)
A(s)
⇒A(s)X1=U(s)=a0X1+a1X2+K+an−1Xn+sXn
=a0X1+a1X2+K+an−1Xn+L{dxn
dt }→(*)
⇒dx1
dt
=x2,dx2
dt
=x3,K,dxn−1
dt
=xn
(*) →dxn
dt
=−a0x1−a1x2−K−an−1xn+u
dx
dt
=
0 1 0 K0
0 0 1 K0
M M M O 0
0 0 0 K1
−a0−a1−a2K−an−1
⎛
⎝
⎜
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
⎟
x1
x2
M
xn−1
xn
⎛
⎝
⎜
⎜
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
⎟
⎟
+
0
0
M
0
1
⎛
⎝
⎜
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
⎟
u
Y(s)=U(s)(b0+b1s+... +bnsn)
A(s)
=b0X1+b1X2+...+bn−1Xn+bnsXn
⇔y=(b0−a0bn)x1+(b1−a1bn)x2+...+(bn−1−an−1bn)xn+bnu
⇔y=(b0−a0bn),(b1−a1bn),...,(bn−1−an−1bn)
( )
x1
M
xn
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
+bnu
A(nxn)
B(1xn)
C(nx1)
D(1x1)
my.dangvan@hust.edu.vn
5 Bai 1 - Chuong 3 - DKLT mien t - Mo hinh toan hoc.key - November 12, 2014