III. ĐIỀU KHIỂN LIÊN TỤC
TRONG MIỀN THỜI GIAN
BM Điều Khiển Tự Động
Th.S. Đặng Văn Mỹ
3.4 THIẾT KẾ BỘ ĐIỀU KHIỂN
III. ĐIỀU KHIỂN LIÊN TỤC TRONG MIỀN THỜI GIAN
my.dangvan@hust.edu.vn
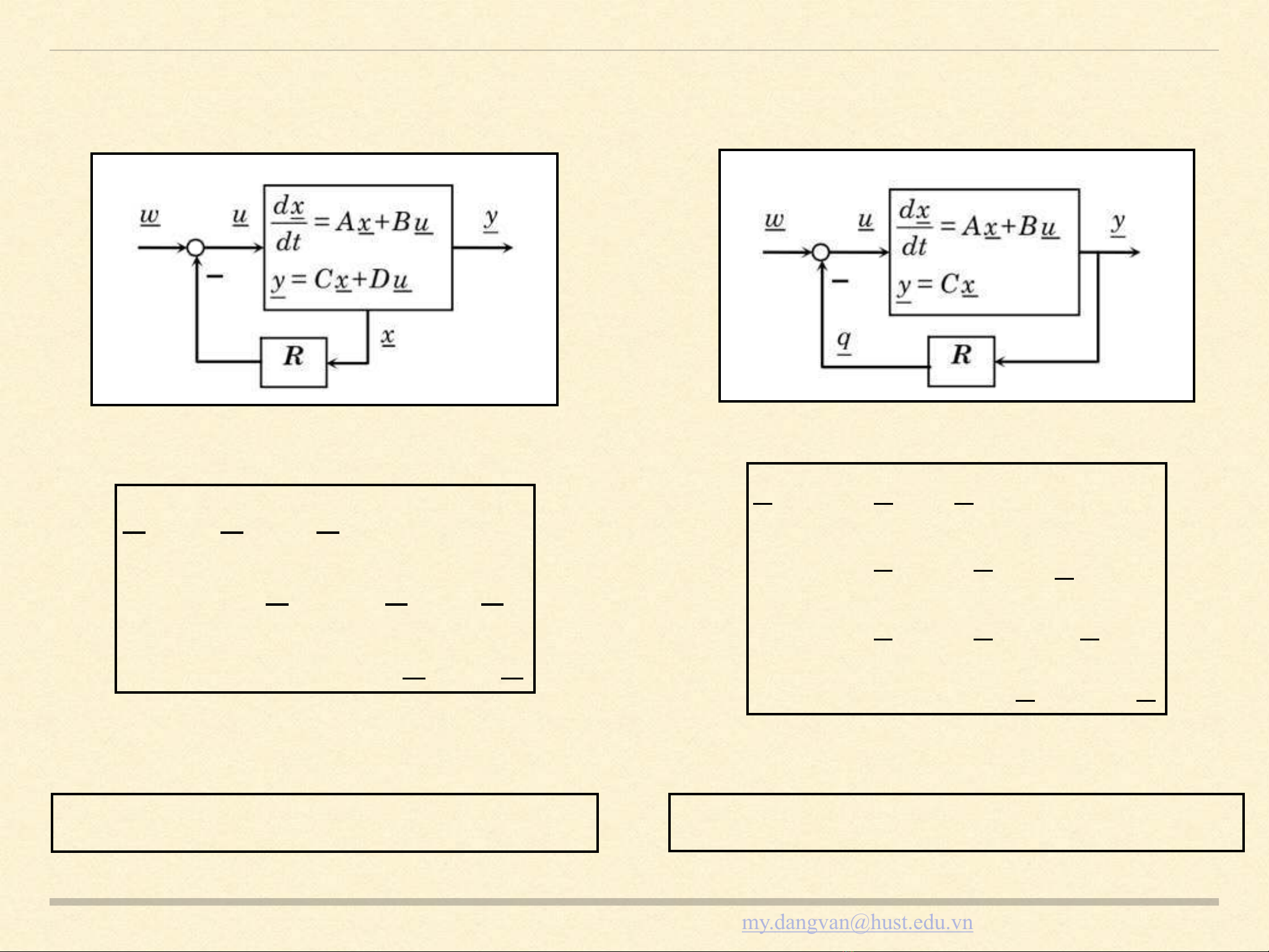
3.4 THIẾT KẾ BỘ ĐIỀU KHIỂN
Phản hồi trạng thái Phản hồi đầu ra
&
x=Ax+Bu
=Ax+B w −Rx
( )
=A−BR
( )
x+Bw
&
x(t)=Ax+Bu
=Ax+B w −Ry
( )
=Ax +B w −RCx
( )
=A−BRC
( )
x(t)+Bw
det sI −A+BR
( )
=(s−s1)(s−s2)K
det sI −A+BRC
( )
=(s−s1)(s−s2)K
Cần xác định ma trận R thỏa mãn:
3.4 THIẾT KẾ BỘ ĐIỀU KHIỂN
my.dangvan@hust.edu.vn
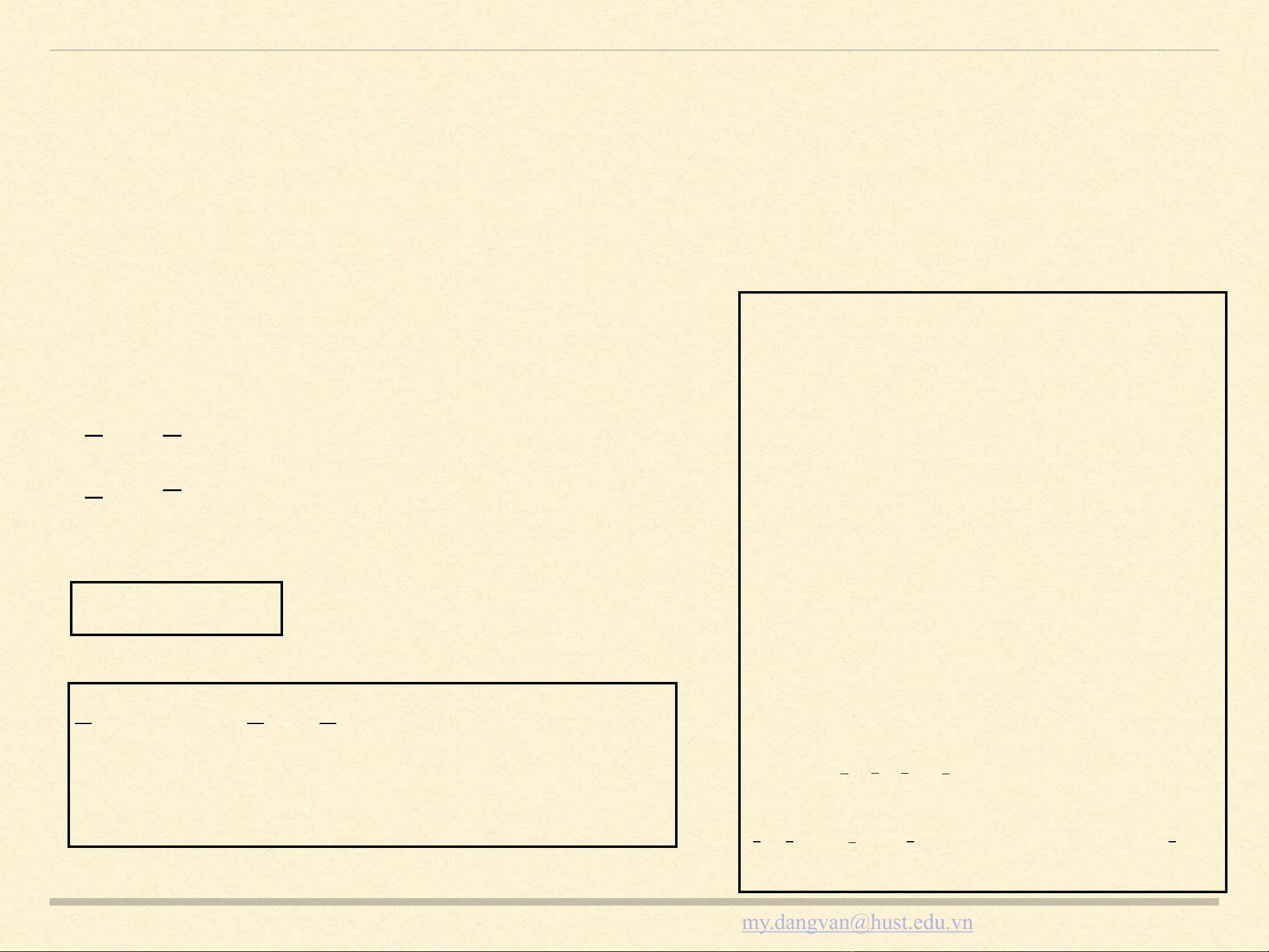
PHƯƠNG PHÁP ACKERMANN
Bước 2: Đưa MHTT về dạng chuẩn điều khiển
&
x=Ax+Bu
y=Cx +Du
⎧
⎨
⎩
Nguyên lý đặt điểm cực là phương pháp xác định ma trận R sao cho hệ
kín có các điểm cực mong muốn.
Đối tượng là hệ một đầu vào và điều khiển được
sT=(0,K,0,1)(B,AB,K,An−1B)−1
⇔sT(B,AB,K,An−1B)=(0,K,0,1)
S=
sT
sTA
M
sTAn−1
⎛
⎝
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
⇒SB =
sTB
sTAB
M
sTAn−1B
⎛
⎝
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
=
0
0
M
1
⎛
⎝
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
SA =
sTA
sTA2
M
sTAn
⎛
⎝
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
=
sTA
sTA2
M
−a0sT−a1sTA−K−an−1sTAn−1
⎛
⎝
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
0 1 0 K0
0 0 1 K0
M M M O 0
0 0 0 K1
−a0−a1−a2K−an−1
⎛
⎝
⎜
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
⎟
S=
010K0
001K0
M M M O 0
000K1
−a0−a1−a2K−an−1
⎛
⎝
⎜
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
⎟
sTA
sTA2
M
sTAn
⎛
⎝
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
=
sTA
sTA2
M
−a0sT−a1sTA−K−an−1sTAn−1
⎛
⎝
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
=SA
z=Sx ⇒&
x=S−1&
z
&
x=Ax+Bu ⇔&
z=SAS−1x+SBu =
0 1 0 K0
0 0 1 K0
M M M O 0
0 0 0 K1
−a0−a1−a2K−an−1
⎛
⎝
⎜
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
⎟
x+
0
0
M
1
⎛
⎝
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
u
Bước 3: Xác định ma trận điều khiển R
&
x=A−BR
( )
x+Bw
⇒det sI −A+BR
( )
=(s−s1)(s−s2)K
=a0+r
1
( )
+a1+r
2
( )
s+K+an−1+r
n
( )
sn−1+sn
Đặt
Đặt ma trận
Ta có
Đổi biến
R=r
1,r
2,..., r
n
( )
Bước 1: Kiểm tra tính ĐK được của đối tượng
Từ phân tích
BỘ ĐIỀU KHIỂN PHẢN HỒI TRẠNG THÁI GÁN ĐIỂM CỰC
3.4 THIẾT KẾ BỘ ĐIỀU KHIỂN
my.dangvan@hust.edu.vn
PHƯƠNG PHÁP ACKERMANN
Bước 2: Đưa MHTT về
dạng chuẩn điều khiển
Đặt
Đặt ma trận
Ta có
Đổi biến
III. ĐIỀU KHIỂN LIÊN TỤC TRONG MIỀN THỜI GIAN
my.dangvan@hust.edu.vn
Hãy tìm ma trận phản hồi trạng thái K sao cho hệ kín có được các điểm
cực mong muốn là