Chương 1
Biến cố ngẫu nhiên và xác suất
Bài 1. Phép thử: 12 hành khách lên 3 toa. Sô TH
có thể: 312
a) A={I: 4, II: 5}. Số TH thuận lợi cho A:C4
12C5
8.
P(A) = C4
12C5
8
312 = 0,05216
b) B={mỗi toa có 4 người lên}. Số TH thuận lợi
cho B:C4
12C4
8.P(B) = C4
12C3
8
312 = 0,0652
c) C={2 người A, B cùng lên 1 toa}. Số TH
thuận lợi cho C:3·1·310.P(C) = 3·1·310
312 =1
3
Chú ý: Trong Mathematica, để tính Ck
n, dùng lệnh
Binomial[n, k]
Bài 2. Phép thử: lấy 5 bi. Số TH có thể: C5
13
A={≥2T}. A={≤1T}. Xét 2 TH
*TH1: 0T. Số TH: C5
7
*TH2: 1T. Số TH: 6·C4
7
Số TH thuận lợi cho A:C5
7+ 6 ·C4
7.PA=
C5
7+ 6 ·C4
7
C5
13
=7
39 = 0,1795.P(A) = 1 −PA=
1−0,1795 = 0,8205
Bài 3. Phép thử: nngười ngỗi ngẫu nhiên vào bàn
(nchỗ). Số TH có thể: n!
a) A={2 người xác định ngồi cạnh nhau}.
Số TH thuận lợi cho A:n·2·(n−2)!.P(A) =
n·2·(n−2)!
n!=2
n−1
b) TH bàn dài. Xét 2 TH:
*TH1: người thứ 1 ngồi đầu bàn. Số TH: 2·1·
(n−2)!
*TH2: người thứ 1 ngồi giữa bàn. Số TH: (n−2) ·
2·(n−2)!
Số TH thuận lợi cho A:2·1·(n−2)! + (n−2) ·
2·(n−2)! = 2 (n−1)!.P(A) = 2 (n−1)!
n!=2
n
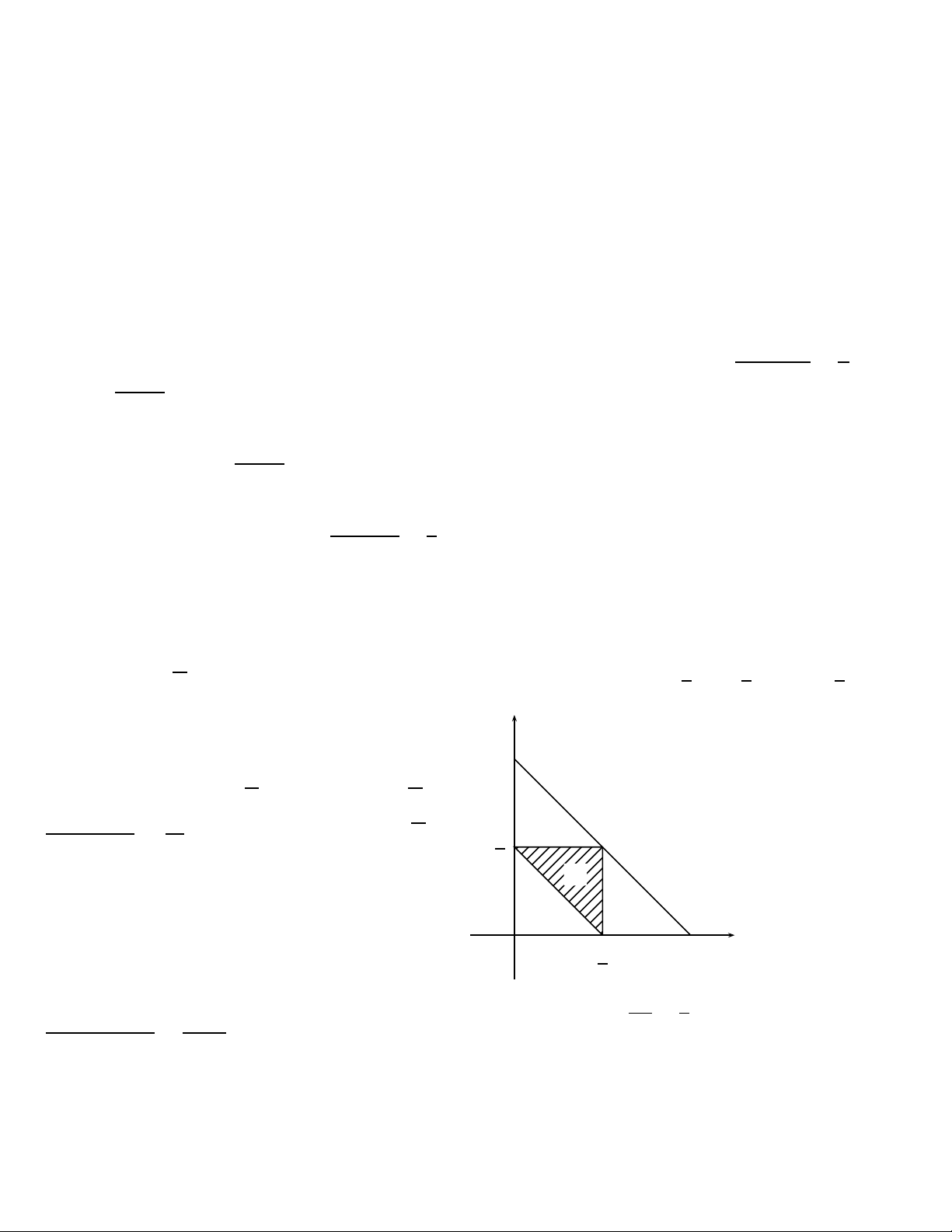
Bài 4. Gọi llà độ dài của thanh; x, y là độ dài 2
đoạn nào đó; đoạn còn lại là l−x−y. Ta có
Ω = {(x, y)∈R2:x, y ≥0, x +y≤l}
Gọi A={(x, y)∈R2:x, y, l −x−ylập thành tam
giác}. Ta có
x < y +l−x−y;y < x +l−x−y;l−x−y < x +y
hay
A={(x, y)∈R2:x < l
2, y < l
2, x +y > l
2}
x
y
Ol
2
l
l
2
l
A
Dễ thấy P(A) = SA
SΩ
=1
4
Bài 5. Ai={người ibắn trúng}, i= 1,2,3,4.
P(A1) = 0,6, P (A2) = 0,7, P (A3) =
0,8, P (A4) = 0,9
A={trên bia có 3 vết đạn}. B={người 1, 2, 3
bắn trúng, người 4 trượt}. Cần tìm P(B|A)
1
B⊂A⇒AB =B=A1A2A3A4.P(AB) =
0,6·0,7·0,8·0,1 = 0,0336
A=A1A2A3A4+A1A2A3A4+A1A2A3A4+
A1A2A3A4
P(A) = 0,6·0,7·0,8·0,1 + 0,6·0,7·0,2·0,9 +
0,6·0,3·0,8·0,9 + 0,4·0,7·0,8·0,9 = 0,4404
P(B|A) = P(AB)
P(A)=0,0336
0,4404 = 0,07629
Bài 6. Ai={người ibắn trúng}, i= 1,2,3.
P(A1) = 0,6, P (A2) = 0,7, P (A3) = 0,8
a) A={chỉ người 2 bắn trúng} = A1A2A3.
P(A) = 0,4·0,7·0,2 = 0,056
b) B={có đúng 1 người bắn trúng} = A1A2A3+
A1A2A3+A1A2A3
P(B) = 0,6·0,3·0,2+0,4·0,7·0,2+0,4·0,3·0,8 =
0,188
c) C={cả 3 đều bắn trúng} = A1A2A3.P(C) =
0,6·0,7·0,8 = 0,336
d)1D={≥1người bắn trúng}
D={cả 3 bắn trượt} = A1A2A3⇒P(D) =
1−PD= 1 −0,4·0,3·0,2 = 0,976
Bài 7. (xem vd3 tr18)Ai={sv ilấy đúng áo}, i=
1,2,3,4
A={≥1 sv lấy đúng áo} = A1+A2+A3+A4
P(Ai) = 1·3!
4! =1
4
P(AiAj) = 1·1·2!
4! =1
12,i < j
P(AiAjAk) = 1·1·1·1
4! =1
24,i < j < k
P(A1A2A3A3) = 1
4! =1
24
P(A) = P(A1) + P(A2) + P(A3) + P(A4)−
P(A1A2)−P(A1A3)−P(A1A4)−P(A2A3)−
P(A2A4)−P(A3A4) + P(A1A2A3) + P(A1A2A4) +
P(A1A3A4)+P(A2A3A4)−P(A1A2A3A4) = 4·1
4−
6·1
12 + 4 ·1
24 −1
24 =5
8= 0,625
1cách 2: D=A1+A2+A3
Bài 8. (sửa “có ≥1 người lấy đúng mũ”: tương tự
bài 7, đáp án: 177
280 = 0,6321)
Bài 9. tương tự bài 2, đáp án: 1−C4
23 + 5C3
23
C4
28
=
79
585 = 0,135
Bài 10. áp dụng 2 kết quả:
*A, B độc lập ⇔P(AB) = P(A)P(B)
*P(A) = 1 −PA
Bài 11. Ai={máy ihỏng}, i= 1,2,3.P(A1) =
0,3, P (A2) = 0,2, P (A3) = 0,1
A={≥2 máy không hỏng} = A1A2A3+A1A2A3+
A1A2A3+A1A2A3
P(A) = 0,7·0,8·0,1 + 0,7·0,2·0,9 + 0,3·0,8·
0,9 + 0,7·0,8·0,9 = 0,902
Bài 12. *H1={lần 1: Đ}, H2={lần 1: T}
P(H1) = 4
9, P (H2) = 5
9
*A={lần 2: Đ, lần 3: T}
P(A|H1) = 3·5
8·7=15
56,P(A|H2) = 4·4
8·7=2
7
P(A) = P(H1)P(A|H1) + P(H2)P(A|H2) = 4
9·
15
56 +5
9·2
7=5
18 = 0,2778
Bài 13. *A1={bi 1 và 2: Đ}, A2= {bi 1 và 2: T},
A={bi 1 và 2 cùng màu} = A1+A2
P(A) = P(A1) + P(A2) = 5·4
11 ·10 +6·5
11 ·10 =5
11
*B={bi 3: Đ}.
P(AB) = P((A1+A2)B) = P(A1B) +
P(A2B) = 5·4·3
11 ·10 ·9+6·5·5
11 ·10 ·9=7
33
Cần tính P(B|A) = P(AB)
P(A)=7/33
5/11 =7
15 =
0,4667
Bài 14. a) * H1={hộp I sang hộp II: 2Đ}
H2={hộp I sang hộp II: 1Đ, 1T}
H3={hộp I sang hộp II: 2T}
P(H1) = C2
6
C2
10
=1
3,P(H2) = 6·4
C2
10
=8
15,
P(H3) = C2
4
C2
10
=2
15
*A={2 bi lấy ở hộp II cùng màu}
P(A|H1) = C2
9+C2
3
C2
12
=13
22,P(A|H2) =
C2
8+C2
4
C2
12
=17
33,P(A|H3) = C2
7+C2
5
C2
12
=31
66
P(A) = P(H1)P(A|H1) + P(H2)P(A|H2) +
P(H3)P(A|H3) = 1
3·13
22 +8
15 ·17
33 +2
15 ·31
66 =
529
990 = 0,5343
b) B={2 bi lấy ở hộp II: 2Đ}. Tương tự a)
P(B|H1) = 6
11,P(B) = 223
495
Cần tính P(H1|B) = P(H1)P(B|H1)
P(B)=
1
3·6
11
223
495
=90
223 = 0,4036
c) Cần tính P(H2A) = P(H2)P(A|H2) = 8
15 ·
17
33 =136
495 = 0,2747
Bài 15. *H1={sp thuộc nm I}, H2={sp thuộc
nm II}, H3={sp thuộc nm III}
P(H1) = 0,4, P (H2) = 0,3, P (H3) = 0,3
*A={sp là phế phẩm}
P(A|H1) = 0,1, P (A|H2) = 0,2, P (A|H3) =
0,15
P(A) = P(H1)P(A|H1) + P(H2)P(A|H2) +
P(H3)P(A|H3) = 0,4·0,1 + 0,3·0,2 + 0,3·0,15 =
0,145
* Cần tính P(H3|A) = P(H3)P(A|H3)
P(A)=
0,3·0,15
0,145 = 0,3103
Bài 16. A4={máy bay có 4 động cơ bay được} =
{≥2 động cơ không hỏng} = {≤2 động cơ hỏng}
P(A4) = C0
4(1 −p)4+C1
4p(1 −p)3+
C2
4p2(1 −p)2= 1 −4p3+ 3p4
Tương tự P(A2) = C0
2(1 −p)2+C1
2p(1 −p) =
1−p2
Máy bay 4 động cơ an toàn hơn 2 động cơ ⇔
P(A4)> P (A2)⇔1−4p3+ 3p4>1−p2⇔p < 1
3
Bài 17. Đặt A={sinh con trai}, p=P(A)
* Trong các gia đình 2 con: B={sinh có trai, có
gái}, C={sinh con 1 bề}
P(B) = C1
2p(1 −p) = 2p(1 −p),P(C) =
C0
2(1 −p)2+C2
2p2=p2+ (1 −p)2
Dễ thấy P(B)≤P(C)(đpcm)
* Trong các gia đình 3 con: tương tự P(B) =
C1
3p(1 −p)2+C2
3p2(1 −p) = 3p(1 −p),P(C) =
C0
3(1 −p)3+C3
3p3= 1 −3p(1 −p)
Với p=1
2thì P(B) = 3
4, P (C) = 1
4nên khẳng
định không còn đúng
Bài 18. Ai={lần ixh mặt sấp}, i= 1,...,10.
P(Ai) = 1
2
A={có 2 chữ giống nhau liền kề nhau}
A=A1A2A3A4. . . A9A10 +A1A2A3A4. . . A9A10
PA=1
29, P (A) = 1 −1
29= 0,998
Bài 19. Phép thử: ncon thỏ vào nlồng. Số TH có
thể: n!
a) A={kthỏ nâu vào klồng màu nâu, n−kthỏ
trắng vào n−klồng trắng}
Số TH thuận lợi cho A:k! (n−k)!
P(A) = k! (n−k)!
n!=1
Ck
n
b) Ai={con thỏ thứ ivào đúng lồng}, i=
1,...,n
A={≥1 con vào đúng lồng} = A1+A2+...+An
(xem vd3 tr18)
đáp án: P(A) = 1 −1
2! +1
3! −...+(−1)n−1
n!
Bài 20. Phép thử: chọn 5 người. Số TH có thể: C5
26
a) A={≥1 bác sĩ}
A={không có bác sĩ}. Số TH thuận lợi cho A:
C18
5
PA=C5
18
C5
26
,P(A) = 1 −PA= 0,8697
b) B={1 bác sĩ, 1 hộ lí, 3 y tá}. Số TH thuận lợi
cho B:8·6·C3
12
P(B) = 8·6·C3
12
C5
26
=48
299 = 0,1605
Bài 21. a) * H1={sp thuộc px 1}, H2={sp thuộc
px 2}, H3={sp thuộc px 3}
P(H1) = 7
16, P (H2) = 5
16, P (H3) = 4
16
*A={sp là chính phẩm}
P(A|H1) = 0,95, P (A|H2) = 0,91, P (A|H3) =
0,85
P(A) = P(H1)P(A|H1) + P(H2)P(A|H2) +
P(H3)P(A|H3) = 7
16 ·0,95+ 5
16 ·0,91+ 4
16 ·0,85 =
0,9125
b) Cần tính P(H1|A) = P(H1)P(A|H1)
P(A)=
7/16 ·0,95
0,9125 = 0,455479
Bài 22. A={lấy được bi đỏ trong kho}, p=
P(A) = 0,5
Số lần thử n= 12
Hi={lấy được ibi đỏ} = {Axảy ra ilần}, i=
0,12
P(Hi) = Ci
npi(1 −p)n−i=Ci
120,512
B={7 lần lấy được 7 bi đỏ} (trong 12 bi, có hoàn
lại)
P(B|Hi) = i
127
P(B) =
12
X
i=0
P(Hi)P(B|Hi) =
12
X
i=0
Ci
120,512 i
127
= 0,0272636
P(H12|B) = P(H12)P(B|H12)
P(B)=C12
12 0,512 ·1
0,0272636 =
0,00895481
Bài 23. P(A+B+C) = P(A) + P(B) +
P(C)−P(AB)−P(AC)−P(BC) + P(ABC) =
P(A)+P(B)+P(C)−P(A)P(B)−P(A)P(C)−
P(B)P(C)+P(A)P(B)P(C) = 0,4+0,5+0,6−
0,4·0,4−0,4·0,6−0,5·0,6 + 0,4·0,5·0,6 = 0,88
Chú ý. Có thể dùng CT P(A+B+C) = 1 −
PA+B+C= 1 −PA B C
Bài 24. *H1={xe lấy được là xe ca}, H2={xe
lấy được là xe con}
P(H1) = 4
7, P (H2) = 3
7
*A={xe lấy được hoạt động tốt}
P(A|H1) = 0,8, P (A|H2) = 0,75
P(A) = P(H1)P(A|H1) + P(H2)P(A|H2) = 4
7·
0,8 + 3
7·0,75 = 0,7786
* Cần tính P(H1|A) = P(H1)P(A|H1)
P(A)=
4/7·0,8
0,7786 = 0,5871
Bài 25. A={một người ủng hộ dự luật}, p=
P(A) = 0.75
B={đa số trong 11 người ủng hộ dự luật} = {A
xảy ra ≥6lần}
P(B) =
n
X
k=6
Ck
npk(1 −p)n−k=
11
X
k=6
Ck
11 ·0,75k·0,2511−k= 0,9657
Chú ý: Trong Math, để tính tổng trên, dùng lệnh
11
X
k=6
Binomial[11,k]∗0.75k∗0.2511−k
Bài 26. *H1={lấy được hộp I}, H2={lấy được
hộp II}, H3={lấy được hộp III}
P(H1) = P(H2) = P(H3) = 1
3
* Phép thử: lấy 1 bi trong hộp chọn được, n= 4
lần thử, A={lấy được bi đen}
P(A|H1) = 3
6= 0,5, P (A|H2) = 2
4=
0,5, P (A|H3) = 2
5= 0,4
*B={≥2Đ}
P(B|H1) = C2
4·0,52·0,52+C3
4·0,53·0,5 + C4
4·
0,54= 0,6875
P(B|H2) = C2
4·0,52·0,52+C3
4·0,53·0,5 + C4
4·
0,54= 0,6875
P(B|H3) = C2
4·0,42·0,62+C3
4·0,43·0,6 + C4
4·
0,44= 0,5248
*P(B) = P(H1)P(B|H1) + P(H2)P(B|H2) +
P(H3)P(B|H3) = 1
3·0,6875 + 1
3·0,6875 + 1
3·
0,5248 = 0,6333
Bài 27. Phép thử: lấy 1 điểm trong hình tròn (O),
n= 5 lần thử, A={điểm nằm trong ∆ABC}
p=P(A) = S∆ABC
S(O)
=
3√3R2
4
πR2=3√3
4π= 0,4134
*B={≥1 điểm nằm trong ∆ABC} = {Axảy
ra ≥1 lần}
B={Akhông xảy ra}. PB= (1 −p)5=
0,0694
P(B) = 1 −PB= 0,9306
Bài 28. Đặt Ai={quả cầu lấy từ hộp ilà đỏ},
i= 1,2,...
P(A1) = m
m+k, P A1=k
m+k
P(A2|A1) = m+ 1
m+k+ 1, P A2|A1=m
m+k+ 1
P(A2) = P(A1)P(A2|A1) + PA1PA2|A1=
m
m+k·m+ 1
m+k+ 1 +k
m+k·m
m+k+ 1 =m
m+k
PA2= 1 −P(A2) = k
m+k
Tương tự, ta dễ dàng quy nạp và kết luận P(Ai) =
m
m+k∀i