QUY LUẬT PHÂN
PHỐI XÁC SUẤT
THƯỜNG GẶP
1
Chương 3
Chương 3
2
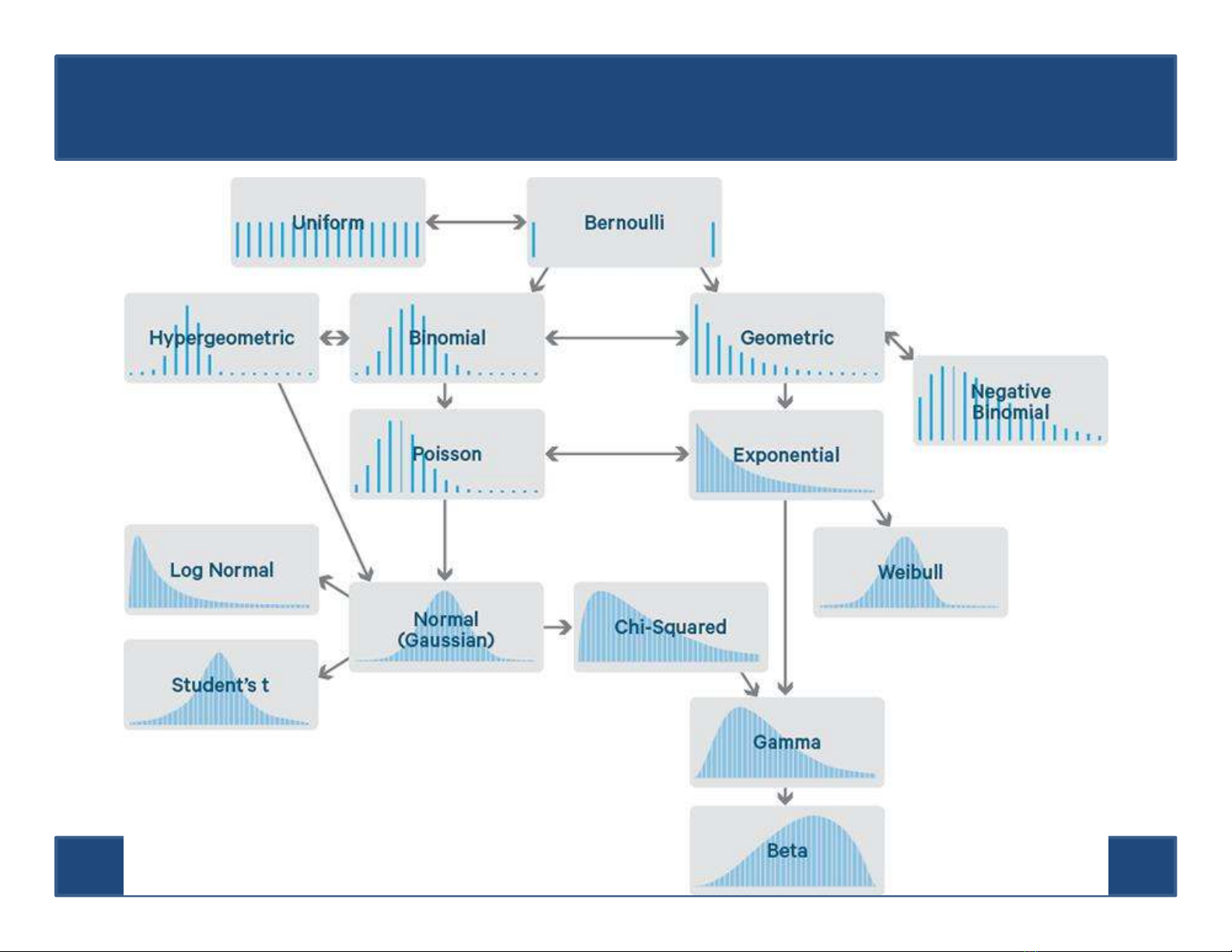
3.1. Biến ngẫu nhiên rời rạc
•Luật “không - một” A(p) Bernoulli
•Luật nhị thức B(n,p) Binomial
•Luật Poisson P() Poisson
•Luật siêu bội H(N,M, n) Hypergeometric
3
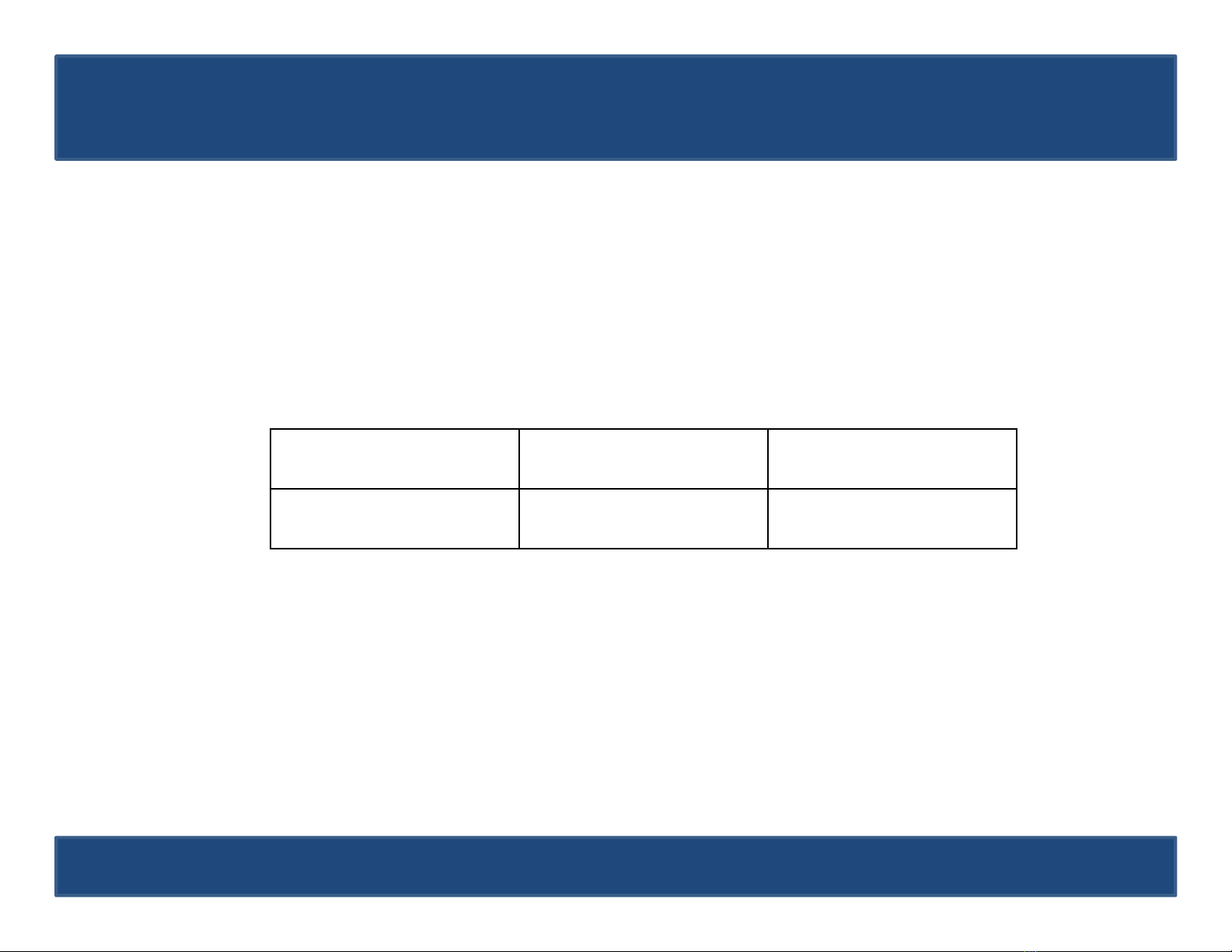
Phân phối Không – một
•Ký hiệu khác: X~A(p)
•Còn gọi là phân phối Bernoulli.
•Bảng ppxs:
•Tham số đặc trưng:
4
X 0 1
P q p
E X p V X pq
Phân phối Nhị thức
Ví dụ mở đầu. Bắn ba viên đạn vào bia. Xác suất bắn
trúng của mỗi viên đều là 0,8. Gọi X là số viên đạn trúng
bia.
Khi đó X nhận giá trị 0,1,2,3. Ta có:
5
1 2
2 1
3 0
0 3
0 0.2 0.2 0.2 1 0.8 0.2
1 3 0.8 0.2 0.2 3 0.8 0.2
2
(
3 0.8 0.8 0.2 3 0.8 0.2
3 0.8 0.8 0.8 1 0.8 0.
)
( )
( )
2( )
P X P
P X P KKT P KTK P TKK
P X P P TKT P KTT
P X P
KKK
TTK
TTT