CHƯƠNG 2
BIẾN NGẪU NHIÊN
MỘT CHIỀU
1
2.1 Khái niệm và phân loại
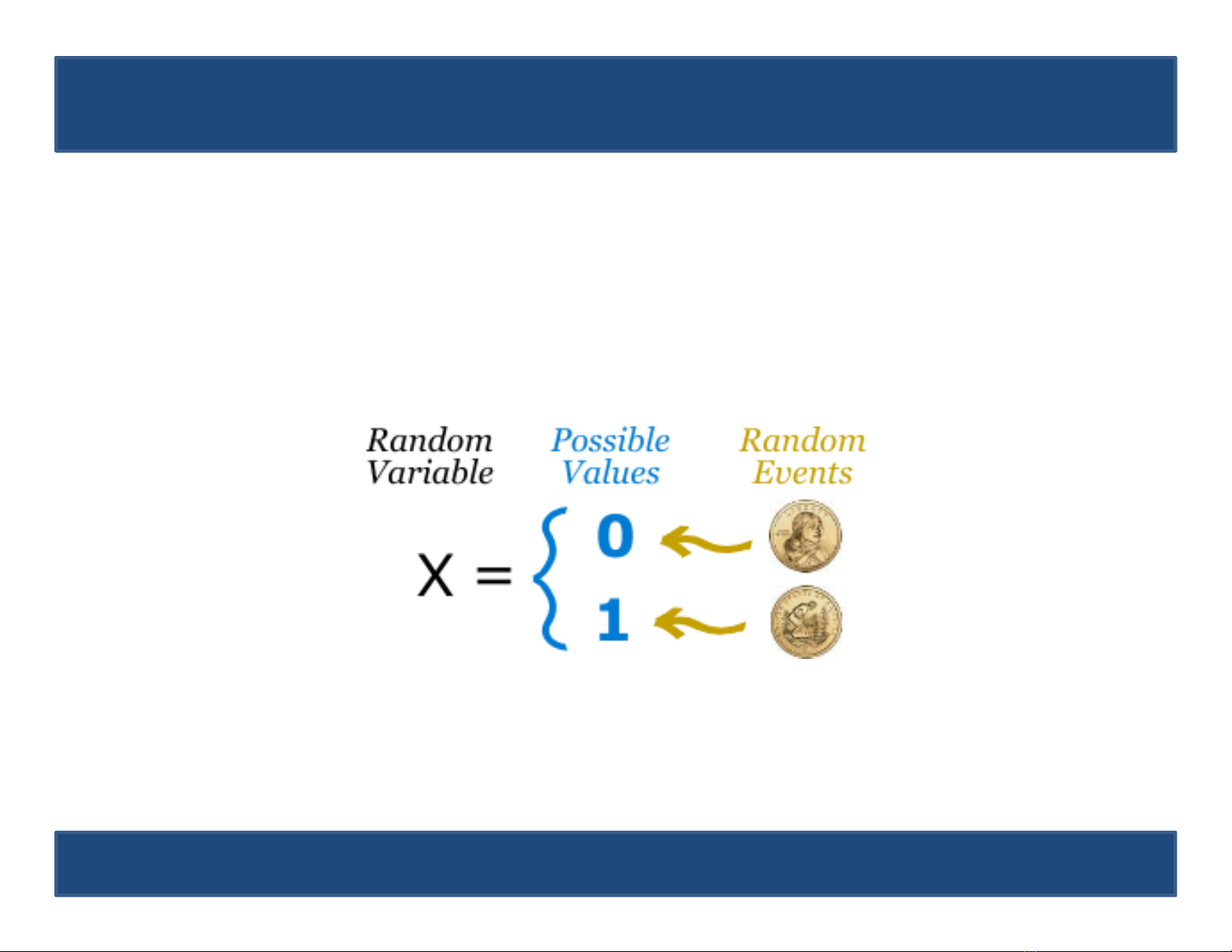
•Khái niệm. Biến số gọi là biến ngẫu nhiên (random
variable) nếu trong kết quả của phép thử nó sẽ
nhận một và chỉ một giá trị có thể có của nó tùy
thuộc vào sự tác động của các nhân tố ngẫu
nhiên.
•Ký hiệu: X, Y, Z … hay X1,X2,…
•Giá trị có thể có của bnn: chữ thường x, y, z, …
•{X≤x} {Y=y} là các biến cố ngẫu nhiên.
2
Ví dụ 1
•X: Lượng khách vào một cửa hàng trong ngày
•Y: Tuổi thọ của một chiếc điện thoại
•Trả ngẫu nhiên 3 mũ bảo hiểm cho 3 người. Gọi Z:
số mũ bảo hiểm được trả đúng người
•T: Số sản phẩm hỏng trong 100 sản phẩm mới
nhập về
•U: Chiều cao của một sinh viên gọi ngẫu nhiên
trong lớp này
3
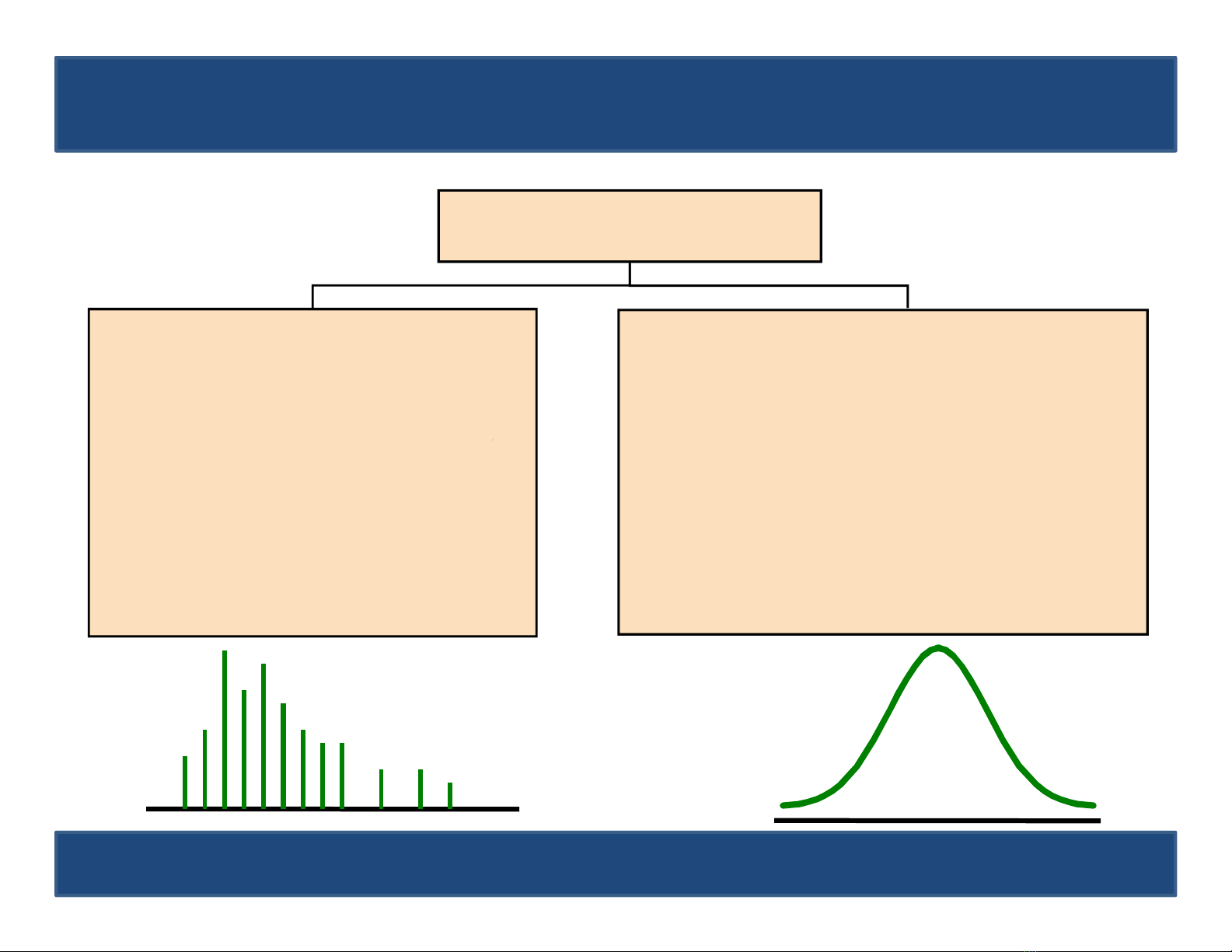
Phân loại bnn
4
Phân loại
5
Rời rạc
- Hữu hạn giá trị
- Vô hạn đếm được giá
trị
- Xác suất tập trung tại
các điểm giá trị
Biến ngẫu nhiên
Liên tục
- Giá trị lấp đầy một hay vài
khoảng hữu hạn hoặc vô hạn
- Xác suất tại từng khoảng giá
trị
- Xác suất không tập trung tại
các điểm
P(X=a)=0 với mọi a