Bài giảng Hàm biến phức và ứng dụng: Chương 1 - Phép tính vi tích phân hàm biến phức

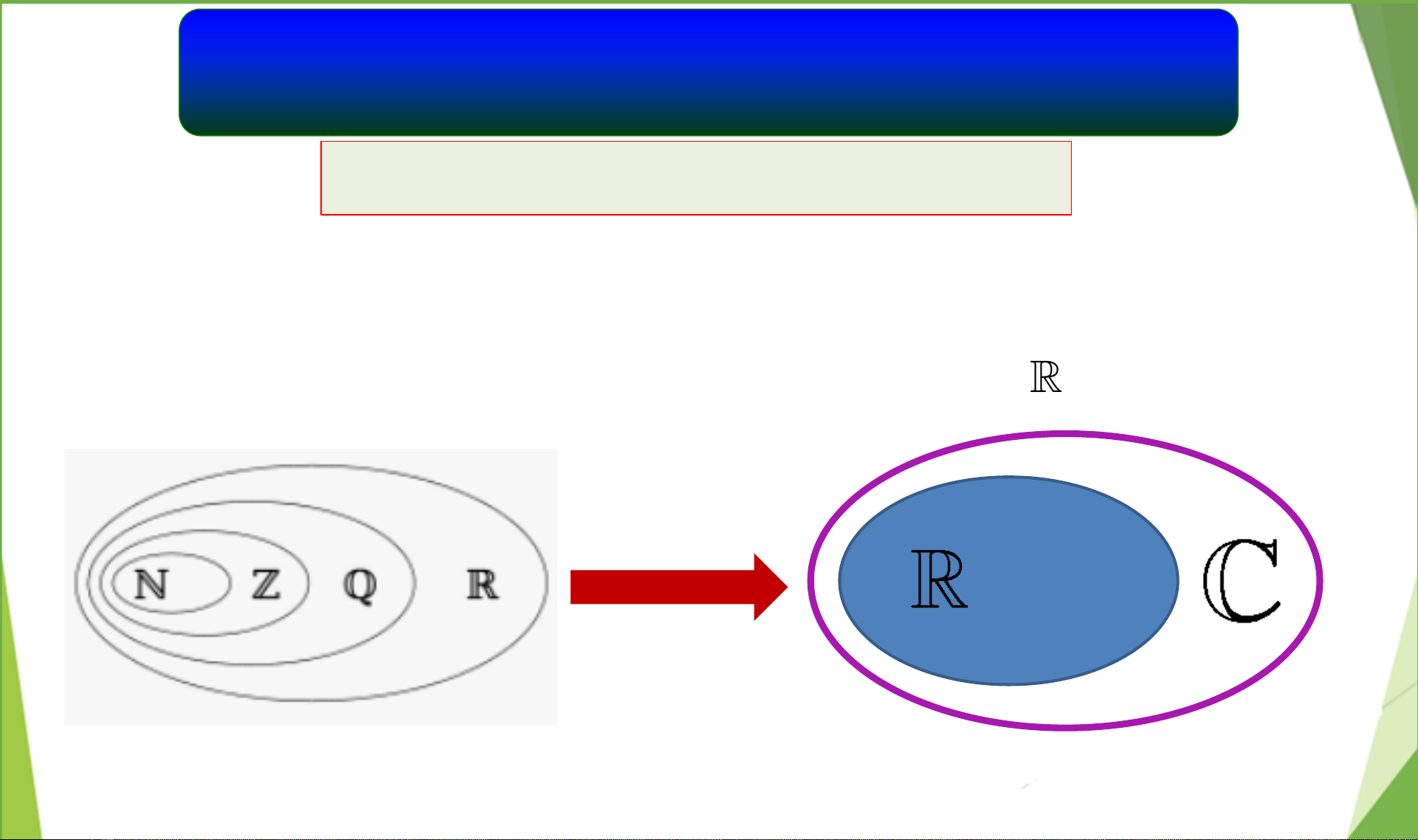
Toán học phổ thông thường giới hạn trong tập hợp số thực, nhưng nhiều bài toán cơ bản, chẳng hạn như giải phương trình đại số như x² + 1 = 0, lại không có nghiệm trong tập số này. Điều này thúc đẩy sự ra đời của số phức, một mở rộng thiết yếu mang đến khung lý thuyết mạnh mẽ hơn cho toán học và các ngành khoa học khác. Tài liệu này cung cấp một cái nhìn tổng quan về các khái niệm cơ bản của hàm biến phức, bắt đầu từ sự cần thiết của việc định nghĩa số phức, các dạng biểu diễn và các phép toán cơ bản. Mục tiêu là trang bị nền tảng vững chắc để người học tiếp cận các ứng dụng sâu rộng của chúng trong nhiều lĩnh vực.

Sinh viên đại học ngành Toán học, Vật lý, Kỹ thuật, Khoa học Máy tính và các ngành khoa học tự nhiên khác đang tìm hiểu về Hàm biến phức và Giải tích phức.

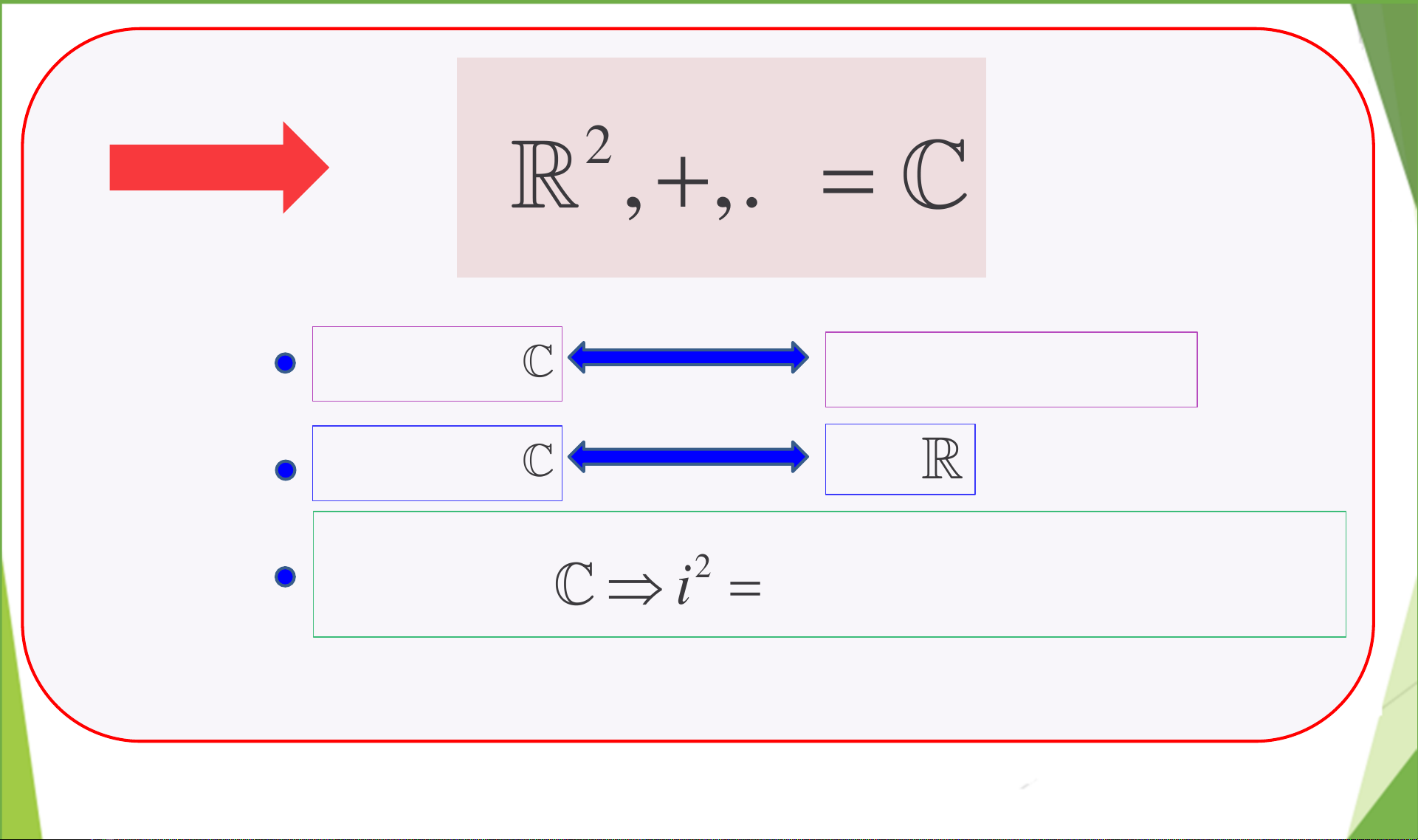
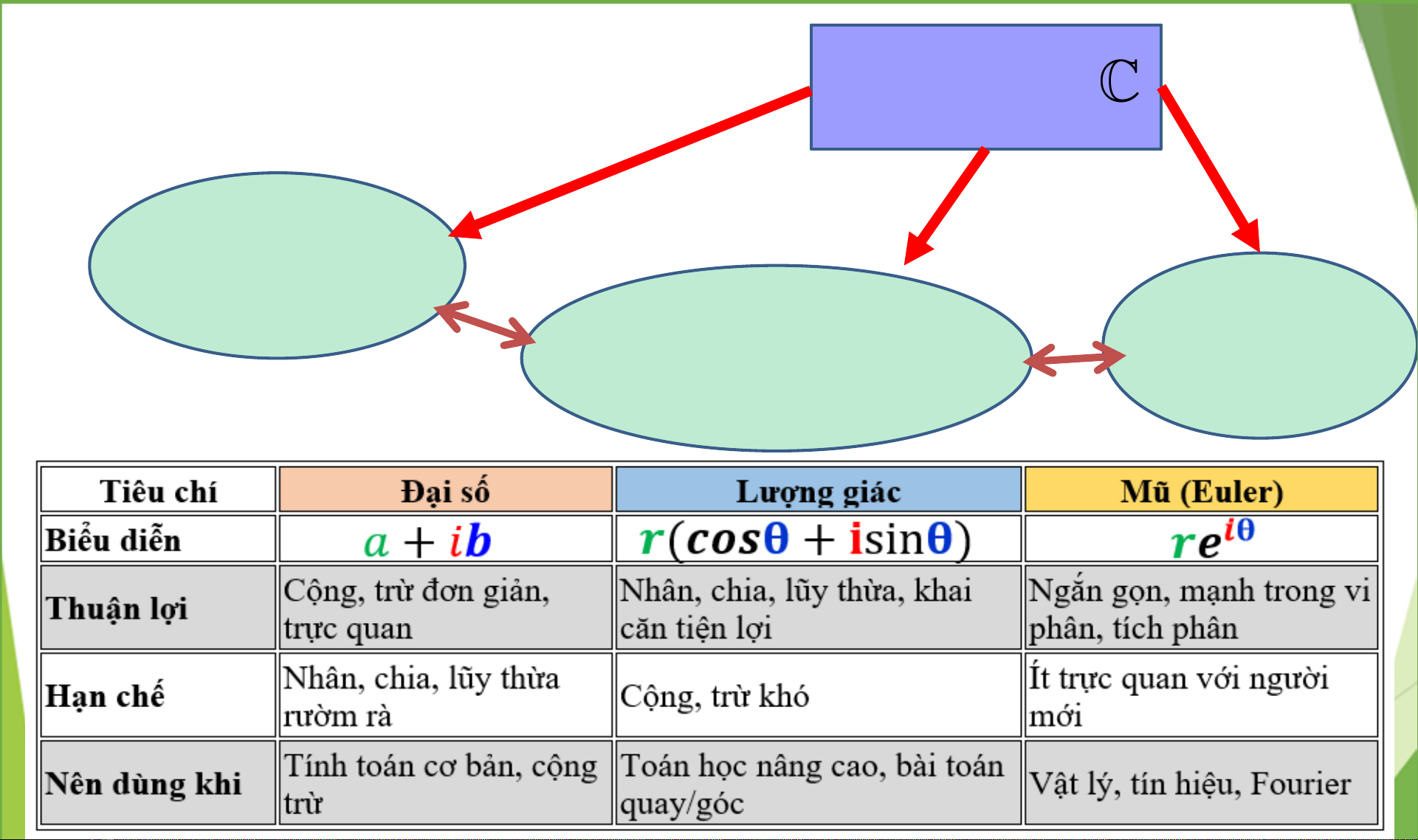
Tài liệu đi sâu vào khái niệm Hàm biến phức, khởi đầu với sự giới thiệu về Số phức như một mở rộng cần thiết của hệ thống số thực, nhằm giải quyết các phương trình không có nghiệm thực. Nó trình bày cách định nghĩa số phức trên không gian R², cùng với các quy tắc cho Phép cộng và Phép nhân. Phần trọng tâm tiếp theo là các Dạng biểu diễn số phức khác nhau: dạng đại số (a+ib), dạng lượng giác (r(cosφ+isinφ)) và dạng mũ Euler (re^iφ), phân tích ưu nhược điểm của từng dạng trong việc thực hiện các phép toán. Tài liệu hướng dẫn chi tiết cách tìm mô đun và argument chính của số phức, yếu tố then chốt để chuyển đổi giữa các dạng biểu diễn. Các ví dụ minh họa cụ thể được cung cấp để thực hành các phép toán cơ bản như cộng, trừ, nhân, chia, cũng như chuyển đổi dạng, tìm căn bậc n và giải phương trình bậc hai với hệ số phức. Đặc biệt, nó ứng dụng Định lý De Moivre để tính lũy thừa và căn của số phức một cách hiệu quả. Nhấn mạnh tầm quan trọng của các phương pháp này trong việc giải quyết các bài toán phức tạp hơn, từ đó cung cấp nền tảng vững chắc cho việc nghiên cứu sâu hơn về giải tích phức và các ứng dụng trong kỹ thuật, vật lý và khoa học máy tính.