Hàm Green
Phương trình Dyson
Trọng Nghĩa
Nội dung
• Định lý Wick
• Giản đồ Feynman
• Phương trình Dyson
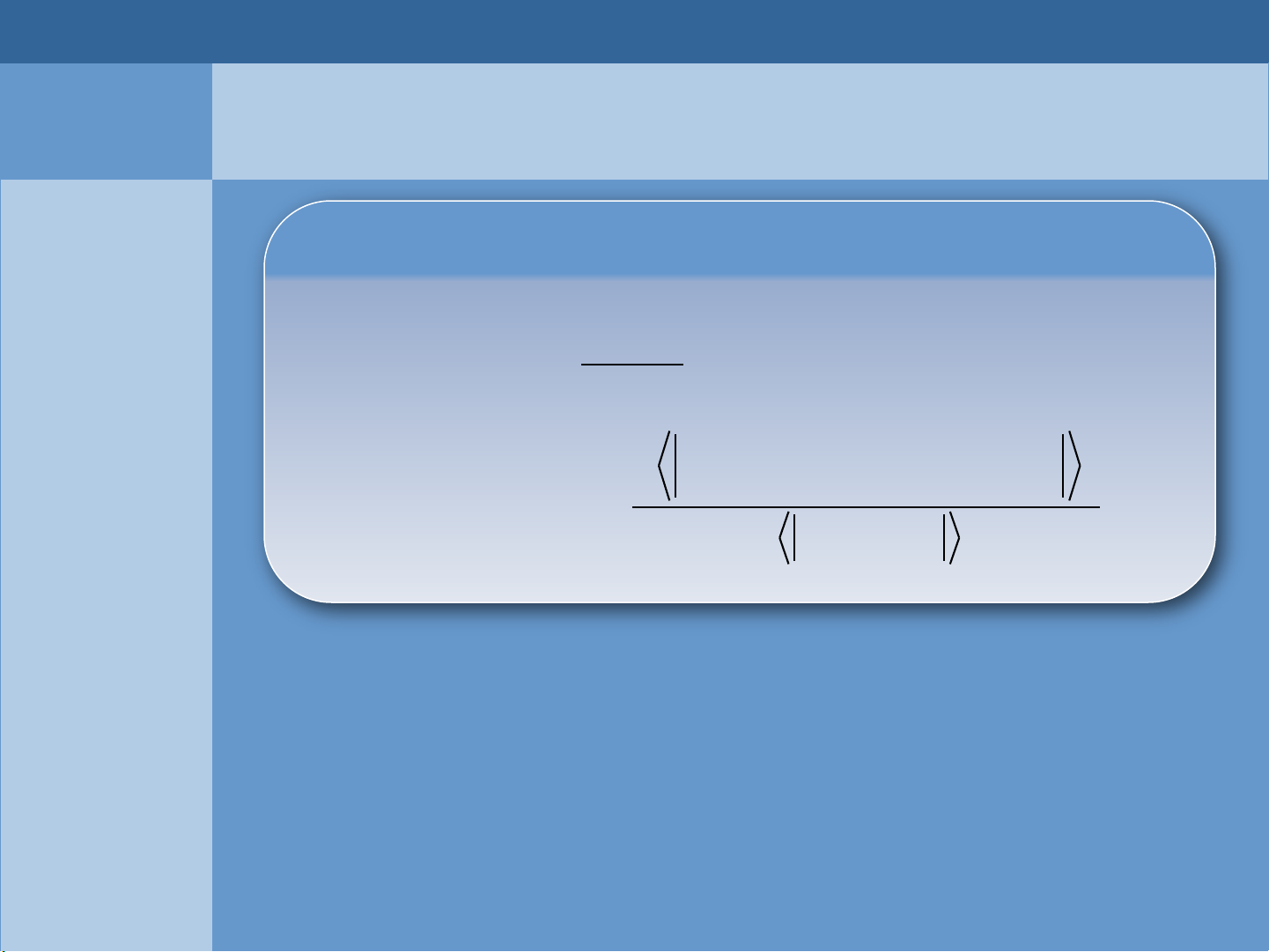
Hàm Green theo khai triển S-Matrận
Định lý Wick
Định lý Wick
Giản đồ
Feynman
Phương trình
Dyson
1
1
0
1
00
00
()
( ; ) ...
!
ˆˆ
ˆˆ
( ) ( )... ( ) ( )
( , )
n
n
n
p n p
i
G p t t dt dt
n
TC t V t V t C t
S





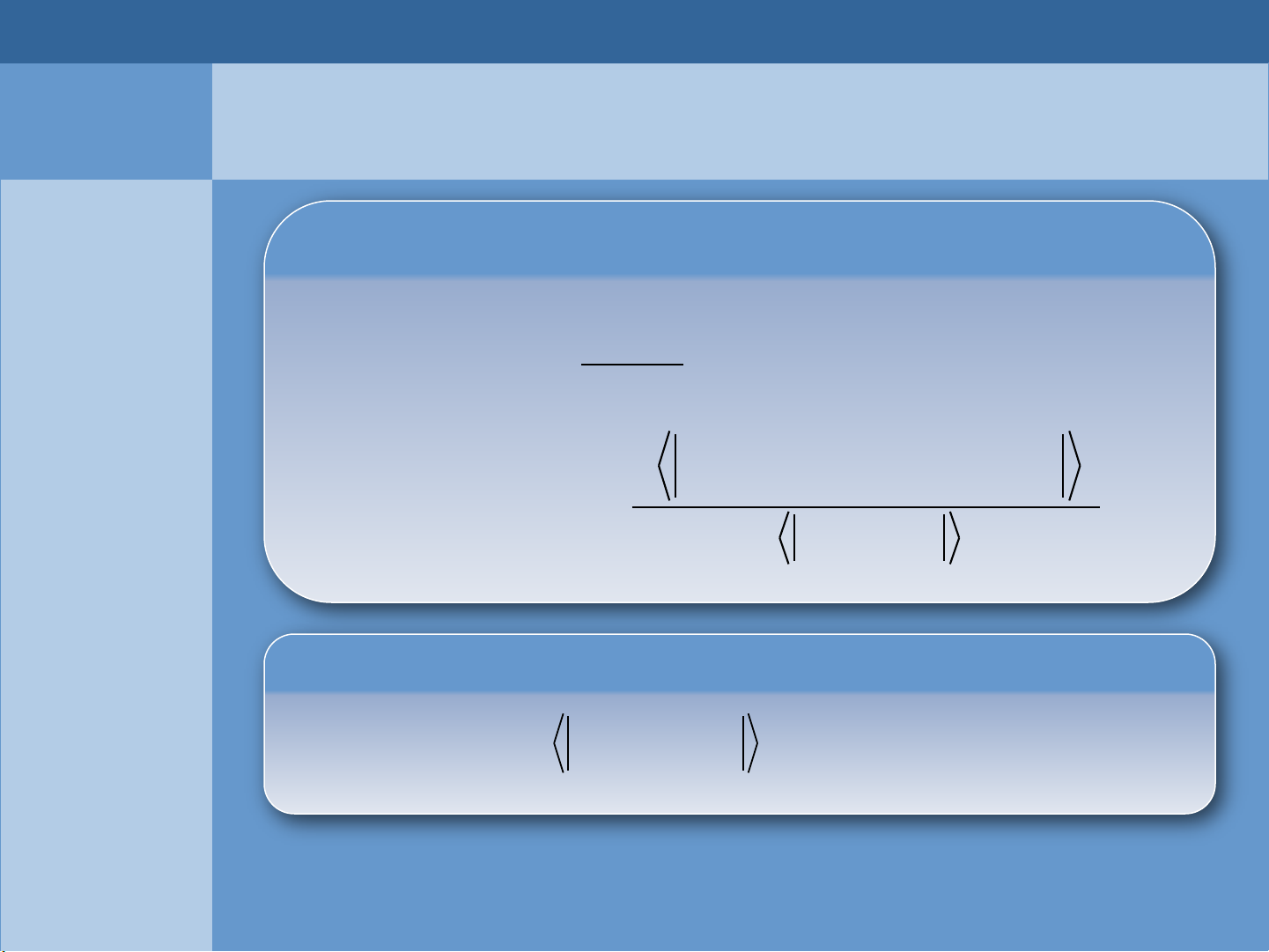
Trong đó
Hàm Green theo khai triển S-Matrận
Định lý Wick
Định lý Wick
Giản đồ
Feynman
Phương trình
Dyson
0
00
ˆˆ
( ) ( ) ( ; )
pp
i TC t C t G p t t

1
1
0
1
00
00
()
( ; ) ...
!
ˆˆ
ˆˆ
( ) ( )... ( ) ( )
( , )
n
n
n
p n p
i
G p t t dt dt
n
TC t V t V t C t
S





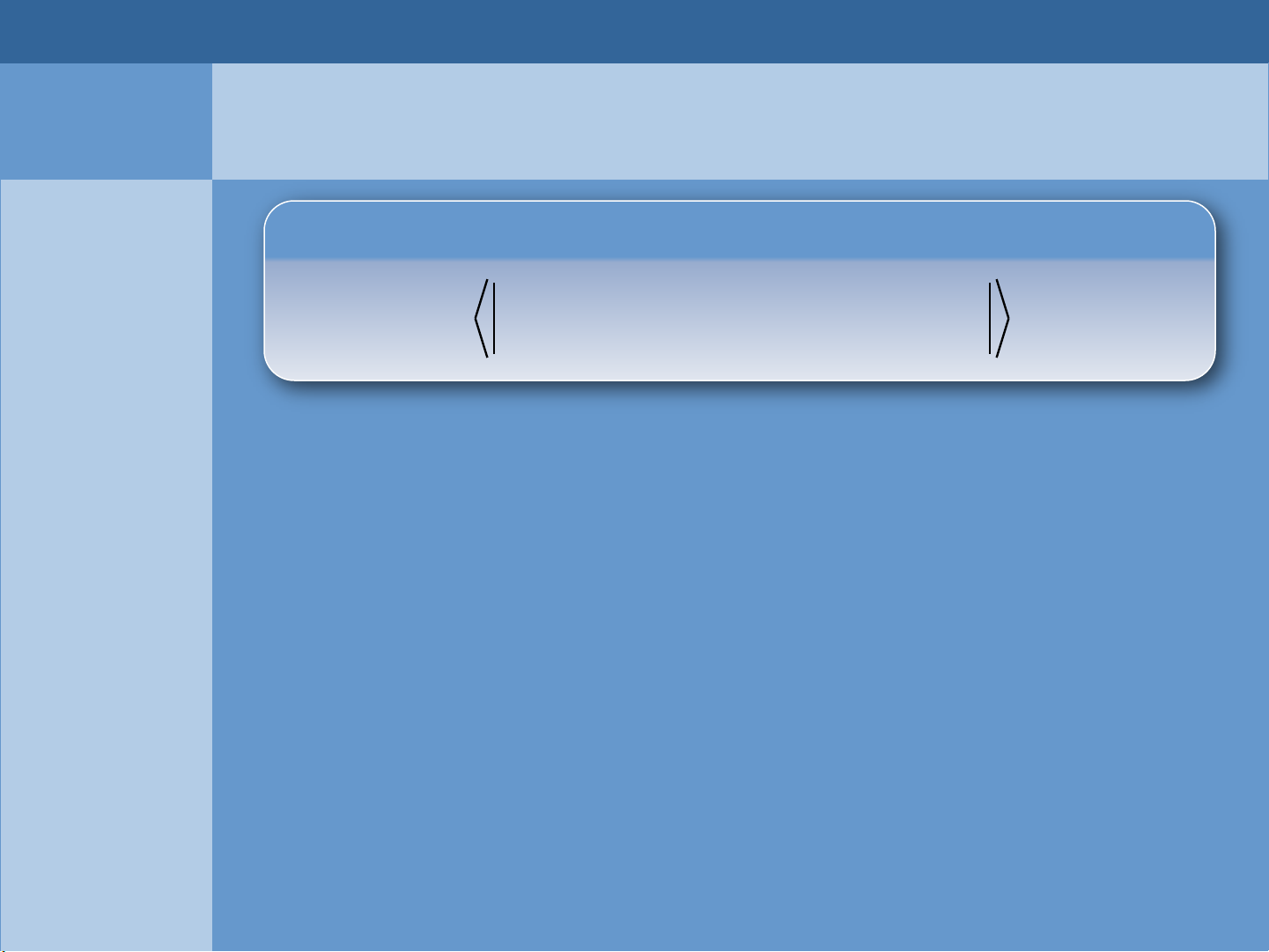
Định lý Wick
Định lý Wick
Giản đồ
Feynman
Phương trình
Dyson
Ta sẽ tập trung vào tính T-tích có dạng như sau
1 2 3
00
ˆˆ
ˆ ˆ ˆ
( ) ( ) ( ) ( ) ( )
pp
TC t V t V t V t C t