Gi¸o ¸n m«n: Lý ThuyÕt §å ThÞ
NguyÔn Minh §øc - §HQG Hµ Néi
60
v1
v2
v10
v5
v8 v9
v6 v7
v3 v4
Chương 6
MỘT SỐ BÀI TOÁN ỨNG DỤNG
(Bài toán tìm đường đi ngắn nhất và bài toán luồng cực đại)
6.1 Bài toán tìm đường đi ngắn nhất
6.1.1 Tìm đường đi ngắn nhất trong đồ thị không có trọng số
Bài toán:
Cho đồ thị không có trọng số G = (V,E) và hai đỉnh u, v ∈V. Tìm đường đi ngắn nhất từ đỉnh u
đến đỉnh v, tức là đường đi từ u đến v có số cạnh (cung) là ít nhất
Để giải quyết bài toán này ta có thể thực hiện theo thuật toán sau đây:
Thuật toán:
Bước 1:
Tại đỉnh u ta ghi số 0
Các đỉnh kề với u (có cạnh đi từ u đến) ta ghi số 1
Các đỉnh kề với các đỉnh đã được ghi số 1 ta ghi số 2
Giả sử ta đã ghi tới i, tức là ta đã đánh số được các tập đỉnh là V(0) = {u}, V(1), V(2),..,V(i). Trong
đó V(i) là tập tất cả các đỉnh được ghi bởi số i. Ta xác định tập các đỉnh được đánh số bởi số i+1 như
sau:
V(i+1) = {x| x ∈V, x∉V(k) với k=0,1,..,i và ∃y∈V(i) sao cho từ y có cạnh (cung) đi tưới x}
Do tính hữu hạn của đồ thị, sau một số hữu hạn bước, thuật toán dừng lại và cho ta tập các đỉnh có
chứa đỉnh v được đánh số bởi m là V(m).
Bước 2:
Do ở bước 1 đỉnh v được đánh số là m, điều này chứng tỏ đường đi từ u đến v có m cạnh (cung) và
là đường đi ngắn nhất từ u tới v. Để tìm tất cả các đường đi có độ dài m ngắn nhất từ u tới v, ta xuất
phát từ v đi ngược về u theo nguyên tắc sau đây:
- Tìm tất cả các đỉnh có cạnh (cung) tới b được ghi số m-1, giả sử đó là xik (k=1,2...).
- Với mỗi đỉnh xik tìm tất cả các đỉnh có cạnh (cung) tới xik được ghi số m-2.
Bằng cách lùi dần trở lại, đến một lúc nào đó gặp đỉnh ghi số 0, đó chính là đỉnh u. Tất cả các đường
đi xác đinh theo các bước trên là đường đi từ u tới v với độ dài m ngắn nhất cần tìm
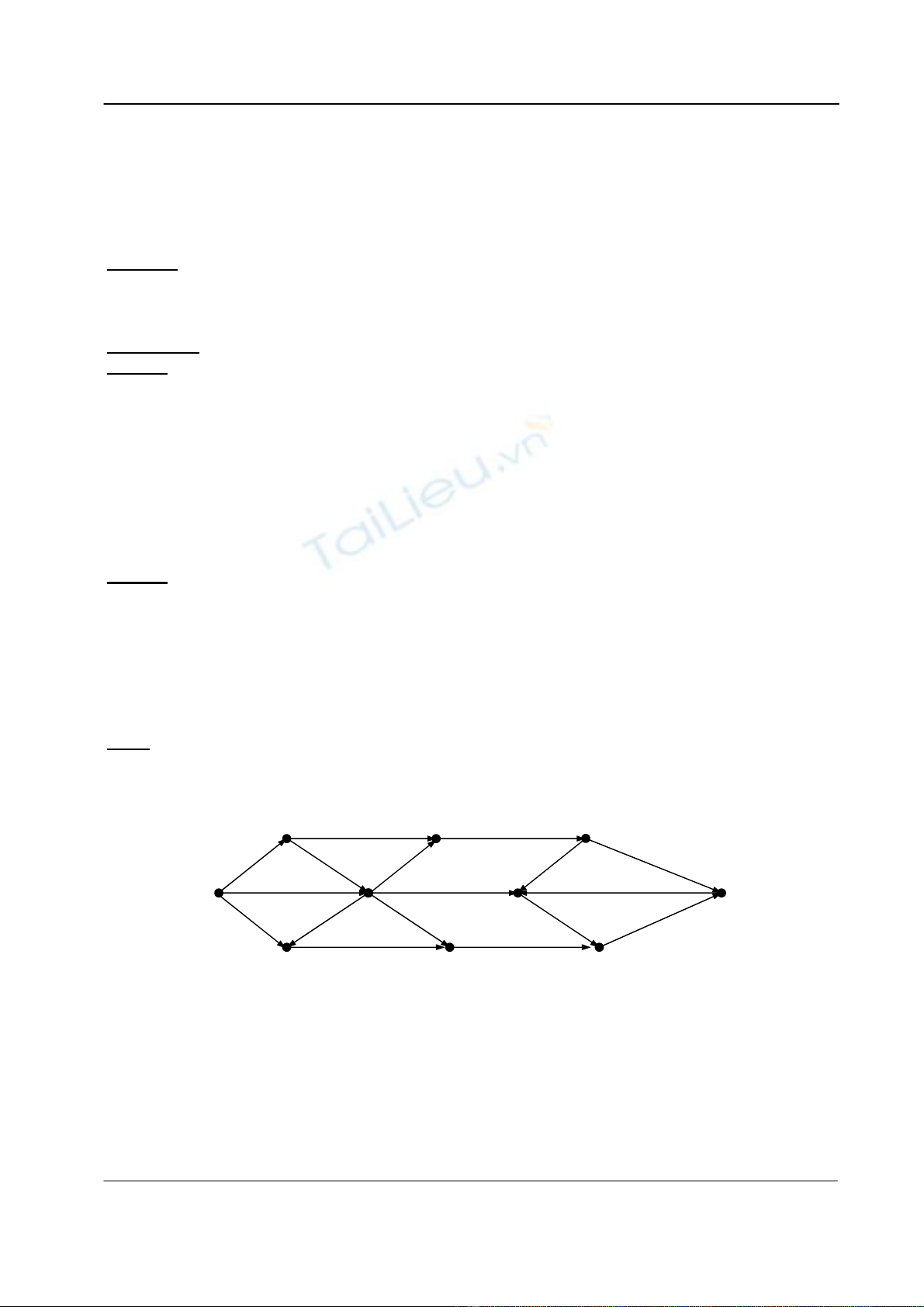
Ví dụ
Xét đồ thị có hướng cho bởi hình dưới đây (Hình 6.1)
Tìm đường đi ngắn nhất từ đỉnh v1 đế
Gi¸o ¸n m«n: Lý ThuyÕt §å ThÞ
NguyÔn Minh §øc - §HQG Hµ Néi
61
Chu ý:
Thuật toán tìm đường đi giữa hai đỉnh u và v trong đồ thị bằng cách áp dụng thuật toán tìm kiếm
theo chiều rộng chính là đường đi ngắn nhất từ u tới v (theo số cạnh).
6.1.2 Tìm đường đi ngắn nhất trong đồ thị có trọng số
Bài toán:
Cho đồ thị có trọng số G = (V,E) và hai đỉnh s, t ∈V. Tìm đường đi ngắn nhất từ đỉnh s đến đỉnh
t, tức là đường đi từ s đến t có tổng trọng số của các cạnh (cung) là nhỏ nhất.
Phần lớn các thuật toán tìm đường đi ngắn nhất từ s đến t được xây dựn trên ý tưởng như sau:
Từ ma trận trọng số c[u,v]; u,v∈V, ta tính cận trên d[v] của khoảng cách từ đỉnh s đến tất cả các
đỉnh v ∈V, mỗi khi phát hiện d[u]+c[u,v]<d[v] thì cận trên d[v] sẽ được làm tốt lên:
d[v]:=d[u]+c[u,v]. Quá trình đó sẽ kết thúc khi tất cả các cận trên d[v] không thể làm tốt lên được
nữa. Khi thực hiện cài đặt trên máy tính, cận trên d[v] được gọi là nhãn của đỉnh v (hay trọng số của
đỉnh v), còn việc làm tốt các cận trên d[v] được gọi là phép gán nhãn cho các đỉnh của đồ thị. Thuật
toán có thể được mô ta như sau:
Bước 1: Đánh trọng số các đỉnh.
Trọng số của đỉnh xuất phát s được đánh trọng số (gán nhãn) d[s] = 0
Tại các đỉnh còn lại ta ghi một số dương đủ lớn sao cho nó lớn hơn trọng số của các đỉnh từ a tới (có
thể dùng ∞)
Bước 2: Thực hiện giảm trọng số các đỉnh
Giả sử tại đỉnh v đang được ghi trọng số d[v]. Nếu tồn tại đỉnh u có trọng số d[u], từ u sang v mà
d[v]>d[u] +c[u,v] thì ta thay trọng số d[v] bởi d’[v]=d[u]+c[u,v]. Trường hợp ngược lại ta giữ
nguyên là d[v]. Quá trình thực hiện cho tới khi trọng số của tất cả các đỉnh đã đạt cực tiểu, tức là
∈∀vV không tồn tại u∈V kề với v mà d[u]+c[u,v]<d[v] .
Bước 3: Xác định đường đi từ s tới t có trọng số nhỏ nhất
Từ bước 2 ta xác định được trọng số của đỉnh t, xuất phát từ t ta đi về đỉnh kề với t, chẳng hạn đó là
đỉnh x có tính chất d[t] = d[x] + c[x,t], nếu không có đỉnh x như vậy thì ta đi về đỉnh kề với t có
trọng số nhỏ nhất, cứ tiếp tục như vậy ta sẽ đi về đến đỉnh y mà đỉnh kề là s sao cho d[y]=d[s]+c[
s,y], với d[s]=0.
Ví dụ
Tuy nhiên, trên thực tế việc tìm đường đi ngắn nhất giữa hai đỉnh lại có rất nhiều trường hợp riêng
biệt mà chưa có một thuật toán nào thực sự tối ưu được tất cả, chẳng hạn đồ thị có trọng số của cạnh
là một số âm, hay đồ thị có chứa chu trình có trọng số âm...Sau đây ta sẽ xét qua môt số trường hợp
riêng.
6.1.2.1 Đường đi ngắn nhất xuất phát từ một đỉnh (Thuật toán Ford – Bellman)
Thuật toán tìm đường đi ngắn nhất từ một đỉnh s đến tất cả các đỉnh còn lại của đồ thị được đưa ra
bởi hai nhà bác học Ford và Bellman, thuật toán này làm việc trong trường hợp trọng số của các
cạnh (cung) là tuỳ ý, nhưng giả thiết rằng trong đồ thị không có chu trình âm.
Gi¸o ¸n m«n: Lý ThuyÕt §å ThÞ
NguyÔn Minh §øc - §HQG Hµ Néi
62
Procedure Ford_Bellman;
(*
Đầu vào: Đồ thị G = (V,E) với n đỉnh,
s
∈V là đỉnh xuất phát, c[u,v] là ma trận trọng số;
Đầu ra: Khoảng cách ngắn nhất từ s đến tất cả các đỉnh còn lại d[v],
Truoc[v] ghi nhận đỉnh đi trước v trong đường đi ngắn nhất từ s đến v;
Giả thiết: Đồ thị không có chu trình âm;
*)
Begin
(* Khởi tạo *)
For v∈V do
Begin
d[v]:=c[s,v];
Truoc[v]:=s;
End;
d[s]:=0;
For k:=1 to n-2 do
For v
∈V\{s} do
For u
∈V do
If d[v]>d[u]+c[u,v] then
Begin
d[v]:=d[u]+c[u,v];
Truoc[v]:=u;
End;
End;
6.1.2.2Tìm đường đi ngắn nhất trong đồ thị có trọng số không âm (thuật toán Dijkstra)
Dijkstra đề nghị một thuật toán tìm đường đi ngắn nhất từ một đỉnh tới tất cả các đỉnh còn lại của đồ
thị. Thuật toán Dijkstra được xây dựng dựa trên cơ sở gán cho các đỉnh các nhãn tạm thời. Nhãn của
mỗi đỉnh cho biết cận trên của độ dài đường đi ngắn nhất từ đỉnh xuất phát đến nó. Các nhãn này sẽ
được biến đổi theo các bước lặp, trong mỗi bước lặp có một nhãn tạm thời trở thành nhãn cố định.
Nếu nhãn của một đỉnh nào đó trở thành cố định thì nó sẽ cho ta độ dài của đường đi ngắn nhất từ
đỉnh xuất phát đến nó. Thuật toán được mô tả cụ thể như sau:
Procedure Dijkstra;
(*
Đầu vào: Đồ thị G=(V,E) với n đỉnh cho bởi ma trận trọng số c[i,j]
s∈V là đỉnh xuất phát
Đầu ra: Khoảng cách từ đỉnh s đến tất cả các đỉnh v còn lại là d[v]
Truoc[v] ghi nhận đỉnh đi trước v trong đường đi ngắn nhất từ s đến v
Giả thiết: Trọng số các cạnh (cung) của đồ thị là không âm
*)
Begin
(* Khởi tao *)
For v∈V do
Begin
d[v]:=c[s,v];
Truoc[v]:=s;
End;
Gi¸o ¸n m«n: Lý ThuyÕt §å ThÞ
NguyÔn Minh §øc - §HQG Hµ Néi
63
d[s]:=0; T:=V\{s}; (* T là tập các đỉnh có nhãn tạm thời *)
(* Bước lặp *)
While T
φ
≠do
Begin
Tìm đỉnh u thuộc T thoả mãn: d[u] = min{d[z]; z thuộc T};
T:=T\{u}; (* Cố định nhãn của đỉnh u *)
for v thuộc T do (*Gán lại nhãn cho các đỉnh *)
if d[v]>d[u] + c[u,v] then
Begin
d[v]:=d[u]+c[u,v];
Truoc[v]:=u;
End;
End;
End;
Ví dụ: