Bài giảng sức bền vật liệu
Chương 2: Lý thuyết về nội lực GV: Lê đức Thanh 06/2015) 1
Chương2
LÝ THUYẾT NỘI LỰC
I. KHÁI NIỆM VỀ NỘI LỰC - P. PHÁP KHẢO SÁT- ỨNG SUẤT
1- Khái niệm về nội lực:
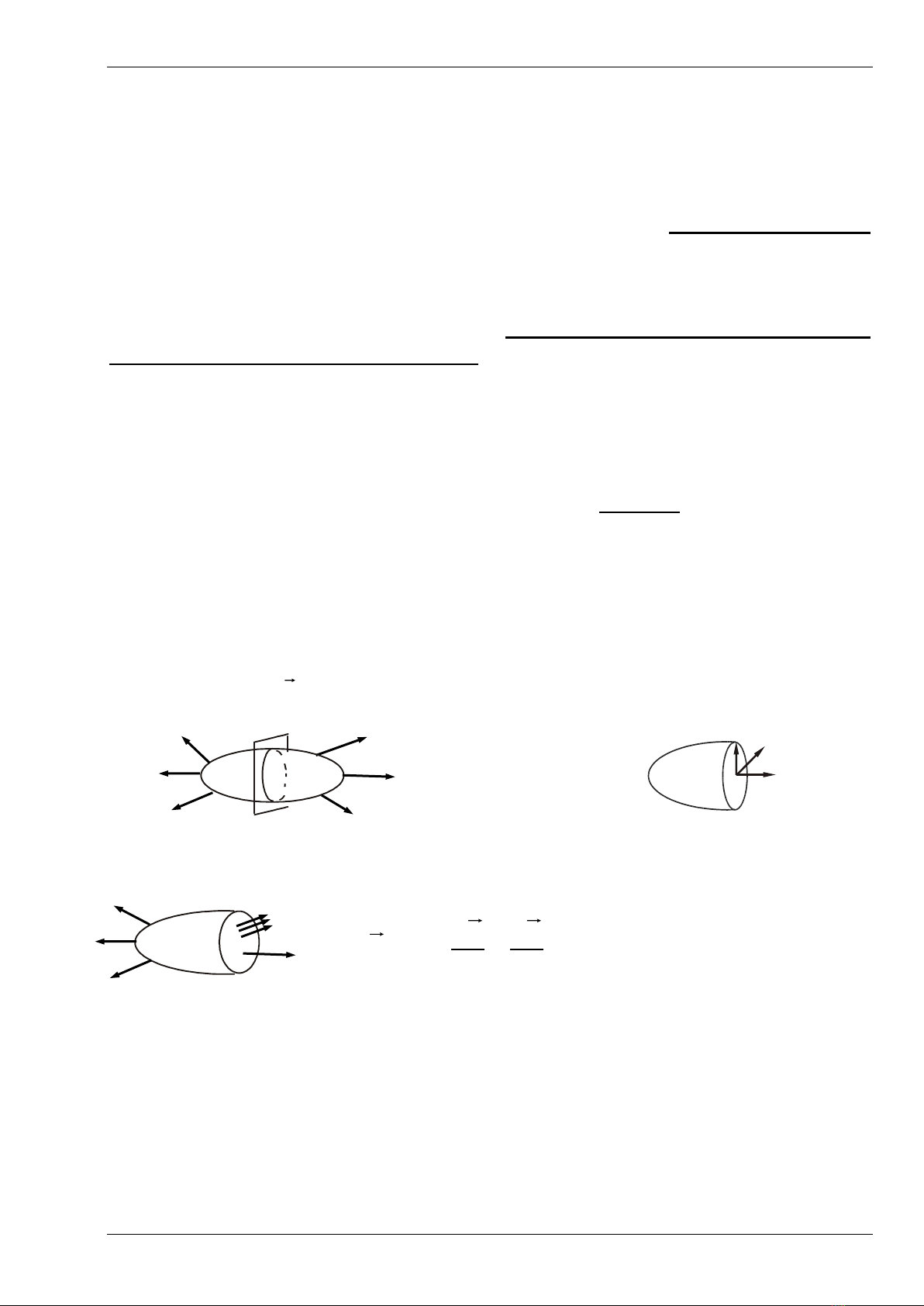
Xét một vật thể chịu tác dụng của ngoại lực và ở trạng thái cân bằng
(H.2.1).Trong vật thể giữa các phân tử luôn có các lực tương tác giữ cho vật thể có
hình dáng nhất định. Khi có ngoại lực tác dụng, các phân tử của vật thể có thể dịch lại
gần nhau hoặc tách xa nhau. Lúc đó, lực tương tác giữa các phân tử của vật thể phải
thay đổi để chống lại các dịch chuyển này. Sự thay đổi của lực tương tác giữa các
phân tử trong vật thể được gọi là nội lực.
Một vật thể không chịu tác động nào từ bên ngoài thì được gọi là vật thể ở trạng
thái tự nhiên và nội lực của nó được coi là bằng không.
2- Khảo sát nội lực bằng phương pháp mặt cắt
Xét vật thể chịu lực cân bằng,để tìm nội lực tại 1 điểm C trong vật thể (H.2.1),Tưởng
tượng một mặt phẳng cắt qua C và chia vật thể thành hai phần A và B; hai phần này
sẽ tác động lẫn nhau bằng hệ lực phân bố trên toàn diện tích mặt tiếp xúc theo định luật
lực và phản lực.Nếu tách riêng phần A thì hệ lực tác động từ phần B vào nó phải cân
bằng với ngoại lực ban đầu (H.2.2).Hệ lực phân bố nầy chính là nội lực trên mặt cắt
đang xét.
3.Ứng suất:
Xét một phân tố diện tích
A bao quanh điểm khảo sát C trên mặt cắt có phương
pháp tuyến v. Gọi
p
là vector nội lực tác dụng trên
A.
Ta định nghĩa ứng suất toàn phần tại điểm khảo sát là :
dA
pd
A
p
pA
0
lim
Thứ nguyên của ứng suất là [lực]/ [chiều dài]2
Thí dụ:(N/cm2, kN/m2…,(1MN/m2 = 1MPa=10daN/cm2)
Ứng suất toàn phần p có thể phân ra hai thành phần:
+ Thành phần ứng suất pháp
v có phương pháp tuyến của mặt phẳng
+ Thành phần ứng suất tiếp
v nằm trong mặt phẳng (H.2.3).
Các đại lượng này liên hệ với nhau theo biểu thức:
222 vvv
p
(2.1)
Ứng suất là một đại lượng cơ học đặc trưng cho mức độ chịu đựng của vật liệu tại
một điểm; ứng suất vượt quá một giới hạn nào đó thì vật liệu bị phá hoại. Do đó,
B
A
P1
P2
P3
P4
Pi
Pn
c
s
n
Hình 2.3 Các thành phần ứng suất
p
t
n
A
A
P
H2.2 Nội lực trên mặt cắt
P1
P2
P3
A
Bài giảng sức bền vật liệu
Chương 2: Lý thuyết về nội lực GV: Lê đức Thanh 06/2015) 2
việc xác định ứng suất là cơ sở để đánh giá độ bền của vật liệu, và chính là một nội
dung quan trọng của môn SBVL.
Thừa nhận (Lý thuyết đàn hồi đã chứng minh)
- Ứng suất pháp
v chỉ gây ra biến dạng dài. (Thay đổi chiều dài)
- Ứng suất tiếp
v chỉ gây ra biến góc. (Thay đổi góc vuông)
II. CÁC THÀNH PHẦN NỘI LỰC TRÊN MẶT CẮT NGANG CỦA THANH &
CÁCH XÁC ĐỊNH
1. Các thành phần nội lực:
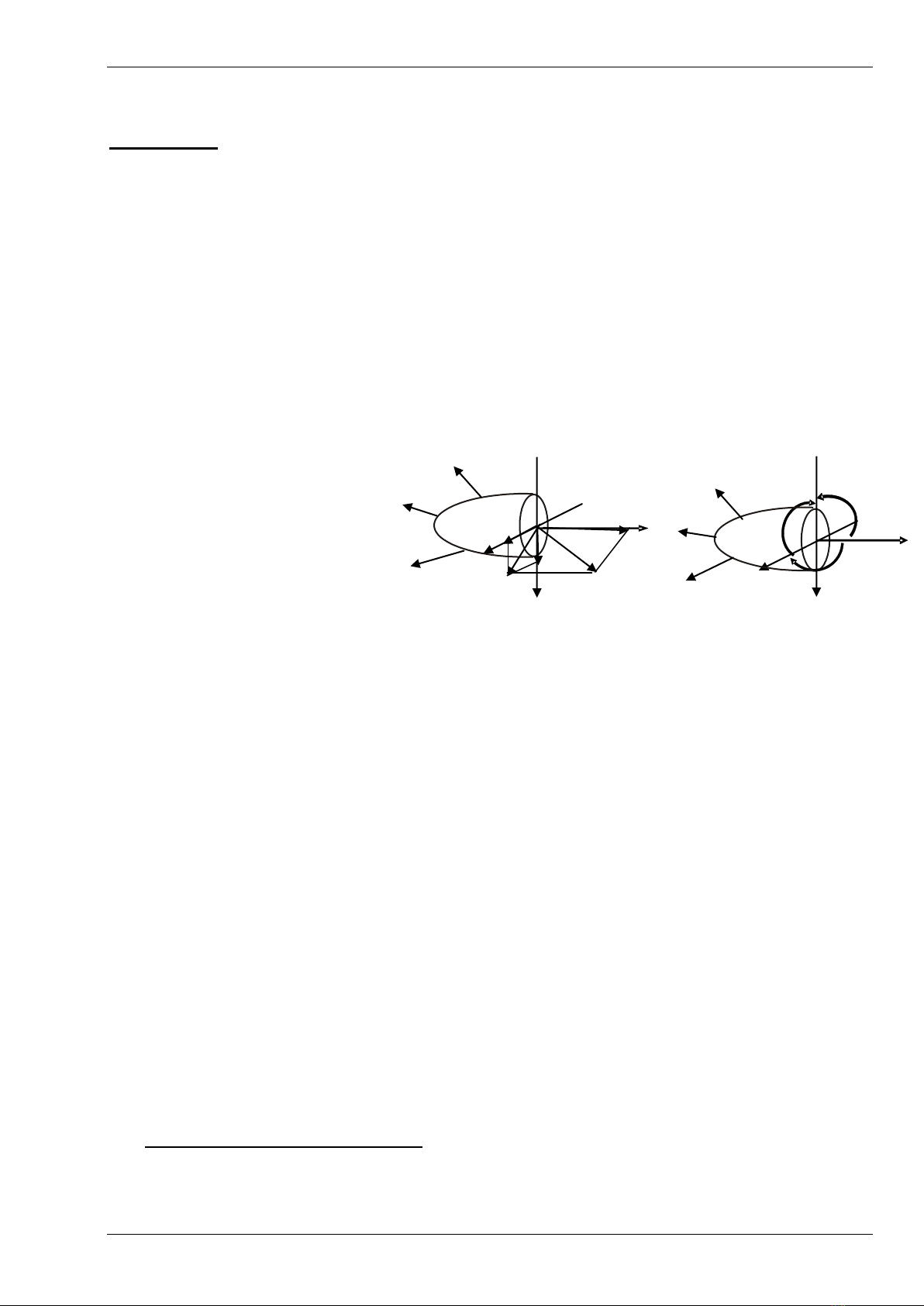
Xét một thanh, đặc trưng bởi mặt cắt ngang A (hay còn gọi là tiết diện) và trục
thanh.
Ở đây ta chưa thể xác định ứng suất ở mỗi điểm trên mặt cắt ngang nhưng hợp lực
của hệ nội lực có thể xác định được (vì tổng hợp lực của nội lực phải cân bằng với tổng
hợp lực của ngoại lực).
Gọi hợp lực của các nội lực
phân bố trên mặt cắt ngang của
thanh là R,với R có điểm đặt và
phương chiều chưa biết.
Đặt một hệ trục tọa độ
Descartes vuông góc ngay tại
trọng tâm mặt cắt ngang, Oxyz,
với trục z trùng pháp tuyến mặt cắt (qui ước theo phương trục thanh,) còn hai trục x, y
nằm trong mặt cắt ngang của thanh (sau nầy sẽ được xác định rõ hơn)
Dời R về trọng tâm 0 của mặt cắt ngang
M Momen
RLuc
có phương bất kỳ
Khi đó, có thể phân tích R ra ba thành phần theo ba trục:
+ Nz theo phương trục z (
mặt cắt ngang) gọi là lực dọc (làm thanh dãn ra, co lại)
+ Qx,và Qy theo phương trục x, hay y (nằm trong mặt cắt ngang) gọi là lực cắt. (vì cắt
ngang thanh)
Mômen M cũng được phân ra ba thành phần xoay quanh 3 trục :
+ Mômen Mx quay quanh trục x gọi là mômen uốn.(Lực tác động
mp(yoz)) làm cho
thanh bị cong trong mp(yoz))
+ Mômen My quay quanh trục y gọi là mômen uốn. (Lực tác động
mp (xoz) làm cho
thanh bị cong trong mp (xoz)
+ Mômen Mz quay quanh trục z gọi là mômen xoắn. (Lực tác động
mp (xoy) làm
cho thanh vặn quanh trục z
Sáu thành phần này được gọi là các thành phần nội lực trên mặt cắt ngang
2- Cách xác định: Sáu thành phần nội lực trên một mặt cắt ngang được xác định từ
sáu phương trình cân bằng độc lập của phần vật thể được tách ra, trên đó có tác dụng
của ngoại lực ban đầu Pi và các nội lực.
Phương trình cân bằng hình chiếu các lực trên các trục tọa độ: trong đó:
Pix, Piy, Piz - là hình chiếu của lực Pi xuống các trục x, y, z.
Các thành phần nội lực
Z
x
R
R/
Qy
Qx
Nz
Mx
Mz
My
z
y
x
y
Bài giảng sức bền vật liệu
Chương 2: Lý thuyết về nội lực GV: Lê đức Thanh 06/2015) 3
Các phương trình cân bằng mômen đối với các trục tọa độ ta có: với:
mx(Pi), my(Pi),mz (Pi) các mômen của các lực Pi đối với các trục x,y, z.
x
n
i
ixx
y
n
i
iyy
z
n
i
izz
QPQX
QPQY
NPNZ
00
00
00
1
1
1
z
n
i
izz
y
n
i
iyy
x
n
i
ixx
MPmMOzM
MPmMOyM
MPmMOxM
0)(/
0)(/
0)(/
1
1
1
3. Liên hệ giữa nội lực và ứng suất:
Các thành phần nội lực liên hệ với các thành phần ứng suất như sau:
- Lực dọc là tổng các ứng suất pháp
- Lực cắt là tổng các ứng suất tiếp cùng phương với nó
- Mômen uốn là tổng các mômen gây ra bởi các ứng suất đối với trục x hoặc y
- Mômen xoắn là tổng các mômen của các ứng suất tiếp đối với trục z
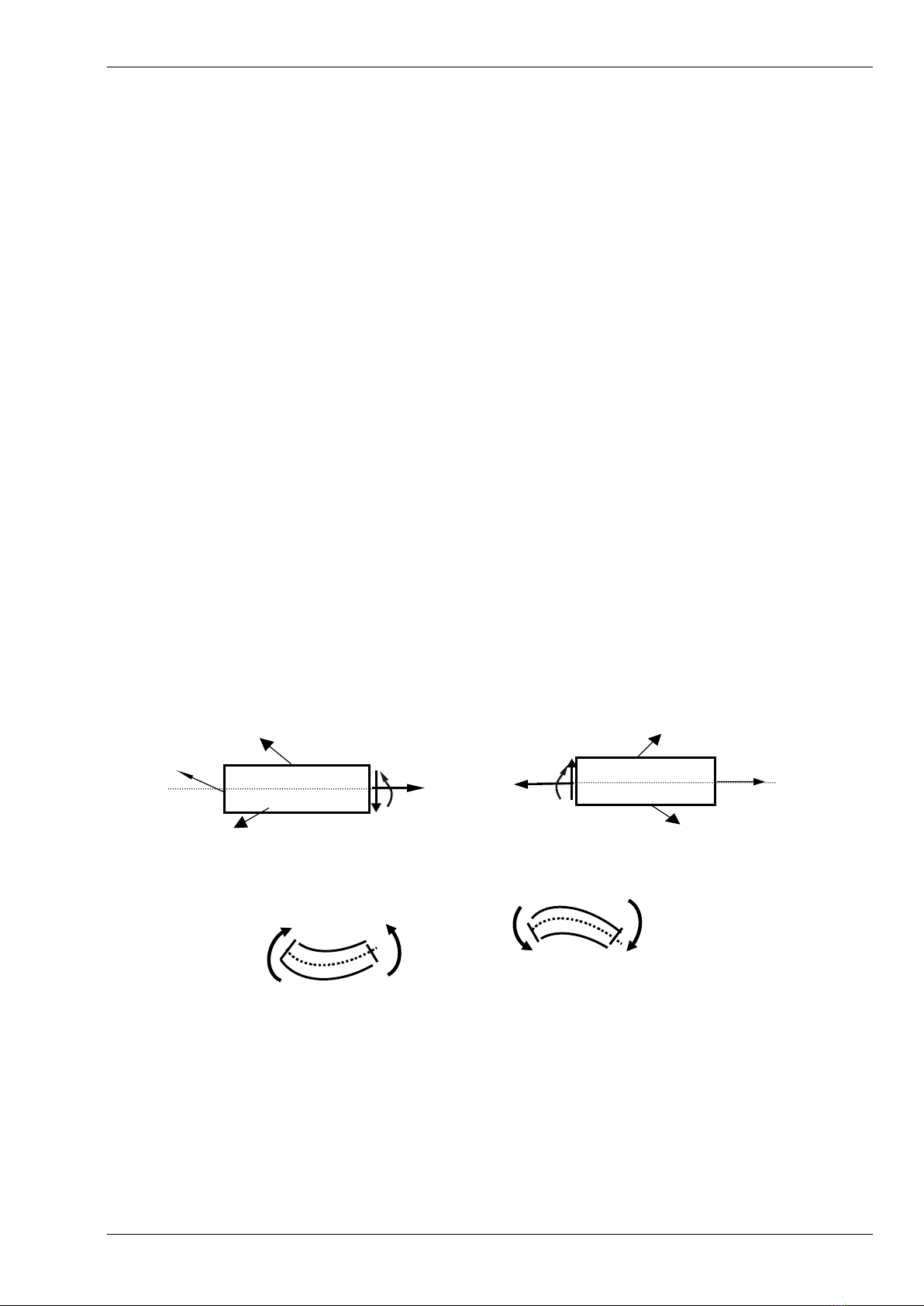
III. BÀI TOÁN PHẲNG (thường gặp)
Trường hợp bài toán phẳng (ngoại lực nằm trong một mặt phẳng (thí dụ mặt phẳng
y0z)), chỉ còn ba thành phần nội lực nằm trong mặt phẳng y0z là : Nz , Qy ,và Mx
Qui ước dấu các thành phần nội lực (H.2.5)
- Lực dọc Nz
0 khi gây kéo đoạn thanh đang xét (có chiều hướng ra ngoài mặt cắt)
-Lực cắt Qy
0 khi làm quay đoạn thanh đang xét theo chiều kim đồng hồ.
- Mômen uốn Mx
0 khi thớ bên dưới thanh bị dãn ra (phía dương của trục y) hay
thớ dưới bị kéo, Và nếu ngược lại là âm. (xét thanh có trục nằm ngang)
Cách xác định:
Dùng 3 phương trình cân bằng tỉnh học, xét cân bằng phần A (hay phần B) bên trái
hay bên phải của mặt cắt để tìm nội lực.
Từ phương trình Z = 0
N
Y = 0 Qy
M/O = 0 Mx
Hình 2.5: Chiều dương các thành phần nội lực
Mx > 0
Nz >o
Qy > 0
P1
P2
A
B
O
O
P3
P4
Pn
Mx > 0
Nz >o
Qy > 0
Mx 0
Mx 0
Mx 0
Mx 0
Mômen M x
0 ,Thanh bị
cong xuống phía dưới
Mômen M x
0 ,Thanh bị
cong lên phía trên
Pi
Bài giảng sức bền vật liệu
Chương 2: Lý thuyết về nội lực GV: Lê đức Thanh 06/2015) 4
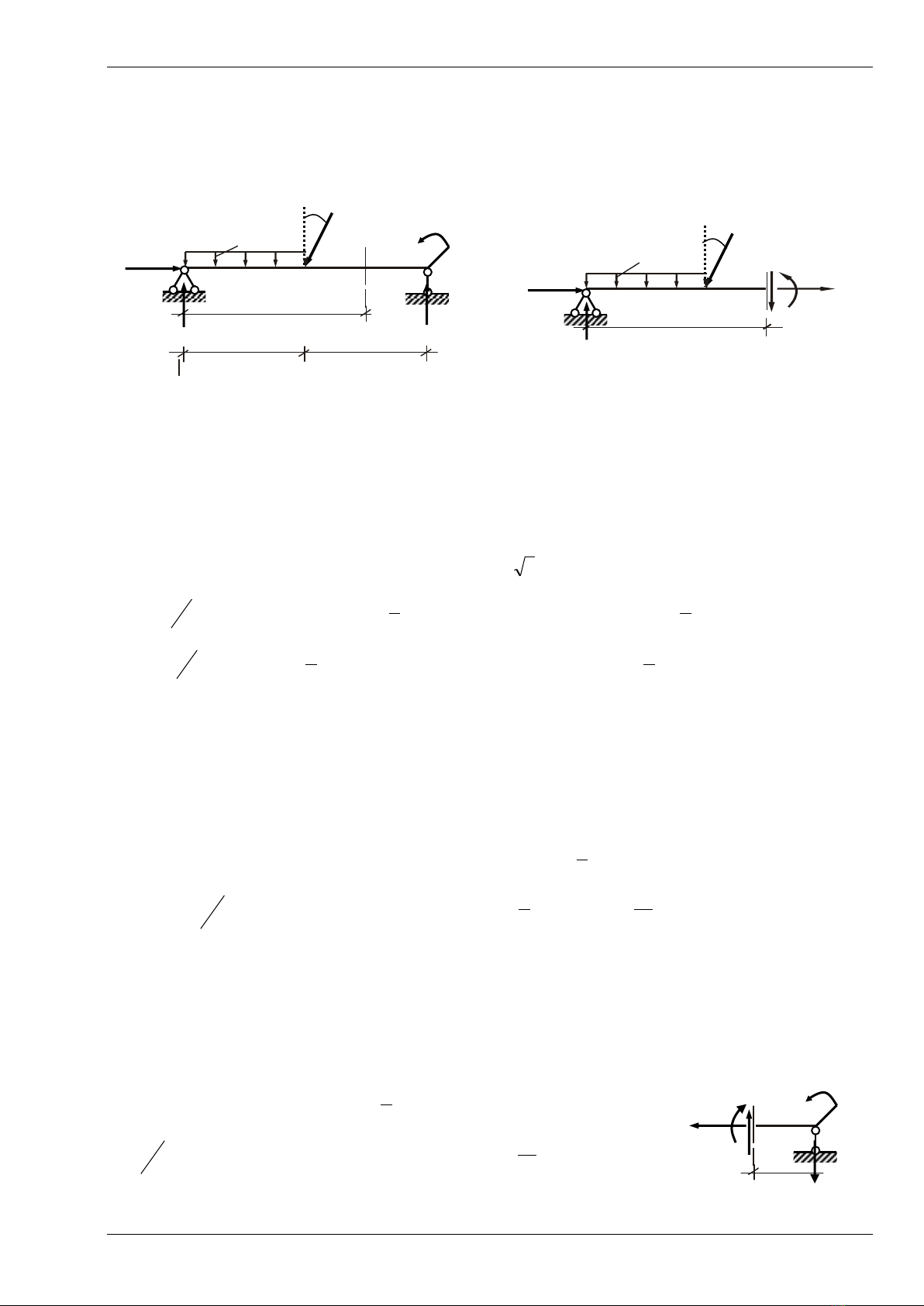
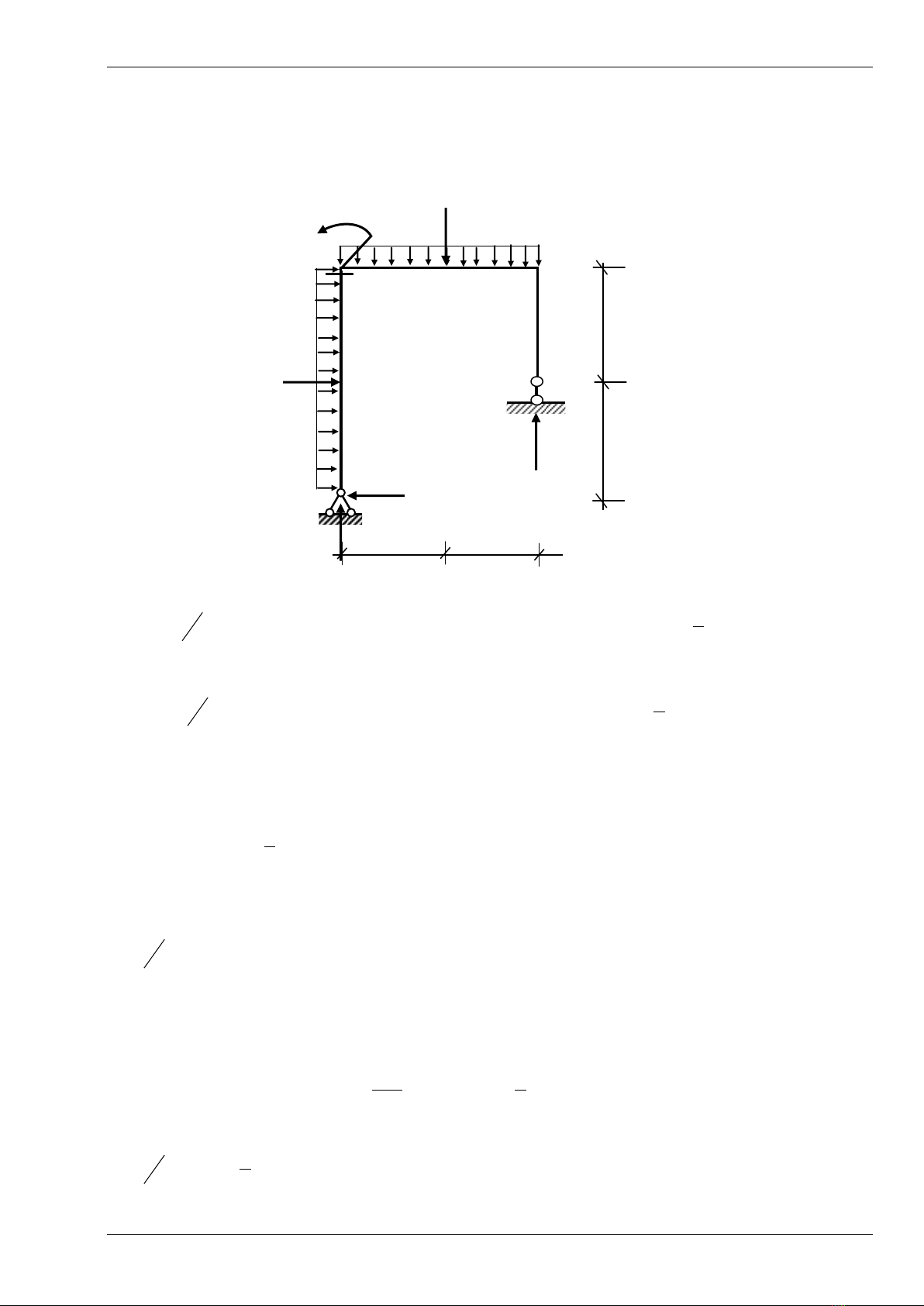
Thí dụ 1. Xác định các thành phần nội lực (hay là nội lực) tại K của thanh thẳng AC
chịu tải trọng phân bố đều q trên đoạn AD và lực tập trung P hợp với phương đứng góc
600 (vị trí của điểm K cho trên hình vẽ). Cho : q = 4kN/m, a = 1m; Mo = 2qa2.
Giải. (Tính toán tất cả bằng chữ trước, cuối cùng mới áp dụng số)
a) Tính các phản lực tại gối tựa:
Giải phóng các liên kết và thay vào đó bằng các phản lực liên kết VA, HA, VC. (giả
sử các phản lực có chiều như hình vẽ)
Viết các phương trình cân bằng tỉnh học khi xét cân bằng thanh AC
kNqaHqaHZ AA 928,630 )cos602(0 0
kNqaVaxVqa
C
MAA 9
4
9
022qa a qa
2
3
60cos20 20
kNqaVaxV
a
qa
A
MCC 1
4
1
022qa- a . Pcos60
2
020
Dấu (- ) cho biết phản lực VC ngược chiều đã chọn ban đầu.
b)Tính nội lực tại K:
Thực hiện mặt cắt 1-1 qua K chia thanh AC làm hai phần. Xét cân bằng của phần
bên trái mặt cắt. Giả sử đặt nội lực theo chiều dương qui ước như hình (H.2.6b) :
kNmqaM
a
qaaqaaVM
O
M
kNqaQPaqaVY
NqaHNZ
xBx
yB
zBz
5,7
8
15
0
2
.5,10
1
4
1
Q 060cos.0
0030cos.20
2
1
y
0
0
Các nội lực đều dương cùng chiều đã chọn.Tại mặt cắt 1-1 Mx dương thanh bị cong
xuống phía dưới (phía bên dưới thanh bị kéo),lực cắt dương từ trên hướng xuống
Nếu xét cân bằng phần phải của thanh, đặt nội lực theo chiều dương qui ước ta tìm
được nội lực như sau.(Vc đặt đúng chiều vừa tính)
kNmqaMqaaVM
O
M
kNqaQVY
NZ
xCx
yC
z
5,7
8
15
025,00
1
4
1
Q 00
00
22
1
y
Thí dụ 2. (tham khảo thêm)
=600
C
M = 2qa2
1
1
k
A
q
P = 2qa
1,5a
a
a
HA
VA
VC
D
VB
H. 2.6b
q
A
1,5a
Qy
M
x
Nz
=600
P = 2qa
HB
D
k
C
M = 2qa2
1
1
k
0,5a
Mx
VC
Qy
Nz
Bài giảng sức bền vật liệu
Chương 2: Lý thuyết về nội lực GV: Lê đức Thanh 06/2015) 5
Cho thanh gãy khúc phẳng ABCDKE chịu tải trọng phân bố đều q trên đoạn ABC và
CDK, lực tập trung P = qa tác dụng tại B và D và momen tập trung M=qa2 đặt tại nút C
a) Tính các phản lực tại A và E.
b) Xác định các nội lực tại mặt cắt 1-1(cho trên hình vẽ)
a) Chọn các phản lực có chiều như hình vẽ
qaVaVqaqaqaqa
A
MEE 2
5
0222qa a - 0 2222
qaHqaqaHNgang AA 30 20
qaVaHaVqaqa
E
MAAA 2
1
022qa 0 222
b) Thực hiện mặt cắt 1-1
Xét đoạn ABC (bên trái) H1a
Chọn chiều các nội lực như hình vẽ . Tìm các nội lực bằng các pt cân bằng
qaNZ z2
1
0
(hằng số và ngược với chiều đã chọn) , Nz hướng vào mặt cắt. Nz
nén trong đoạn AC
00 320
yy QqaqaqaQNgang
(Tại 1-1)
222 3022a3qa 0
0qaMMqaqa
Mxx
(Mx cùng chiều đã chọn , do đó thanh chịu kéo phía bên phải thanh ABC
Xét đoạn CDKE (bên phải) H1b
00
y
QNgang
(Tại 1-1)
qaN
qa
qaqaNungĐzz 2
1
0
2
5
20
(ngược chiều đã chọn).Vậy Nz
hướng vào mặt cắt , lực dọc chịu nén
2222 3022aqa
2
5
0
0qaMMqaqaqa
Mxx
A
VA
q
qa
a
qa2
qa
a
a
a
VE
HA
B
A
C
B
D
B
K
B
E
K
1
B
1
B