CÂY
Nguyễn Quỳnh Diệp
diepnq@tlu.edu.vn
1
CHƯƠNG 6
Nguyễn Quỳnh Diệp
NỘI DUNG
•Các định nghĩa và tính chất
•Các ứng dụng của cây
•Cây khung
•Cây khung nhỏ nhất
Toán rời rạc 2
Nguyễn Quỳnh Diệp
Toán rời rạc 3
6.1. CÁC ĐỊNH NGHĨA VÀ TÍNH CHẤT
Nguyễn Quỳnh Diệp
CÂY
Toán rời rạc 4
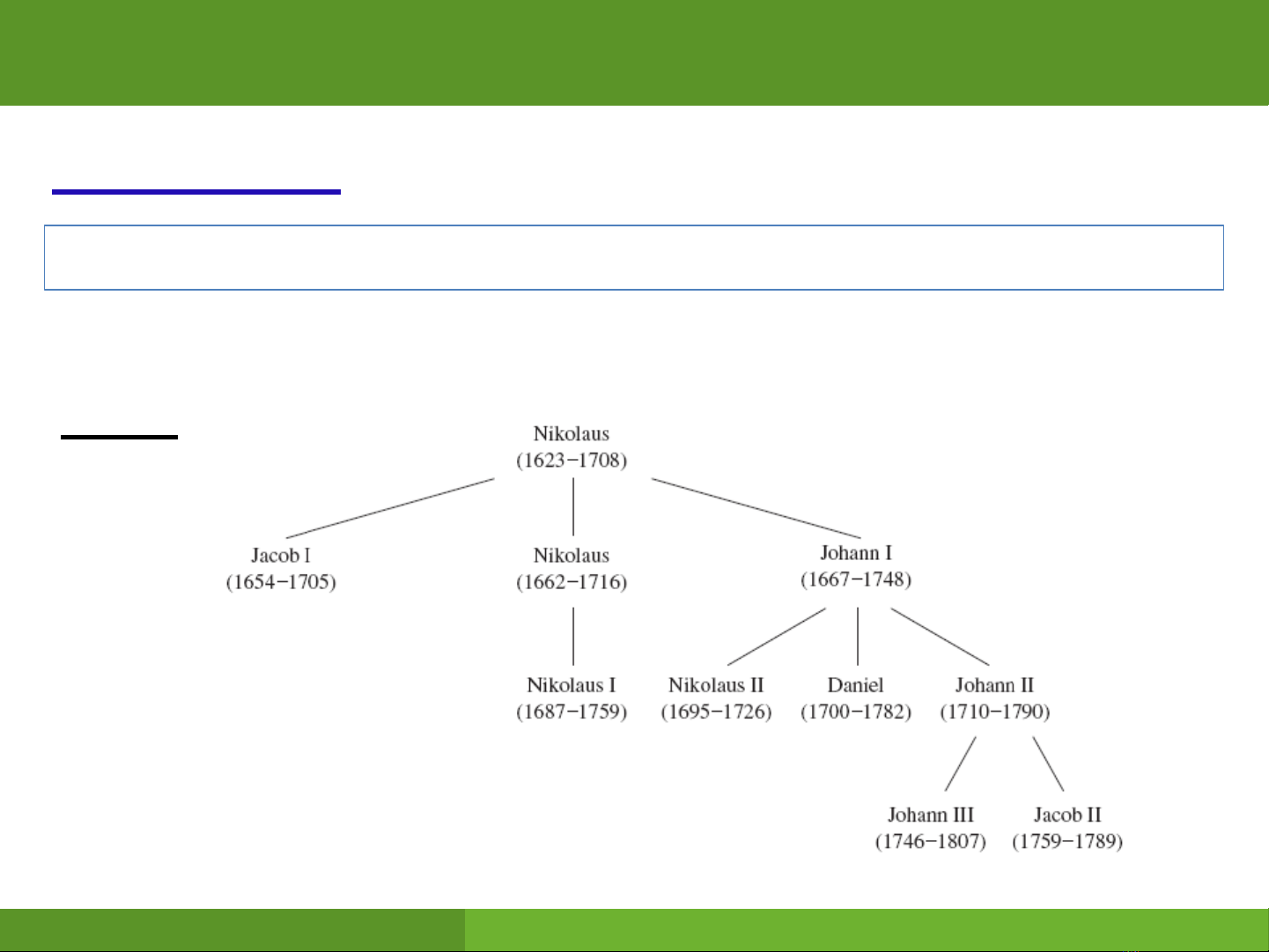
Cây là một đồ thị vô hướng, liên thông và không có chu trình đơn
Định nghĩa 1:
Ví dụ:
Nguyễn Quỳnh Diệp
CÂY
Toán rời rạc 5
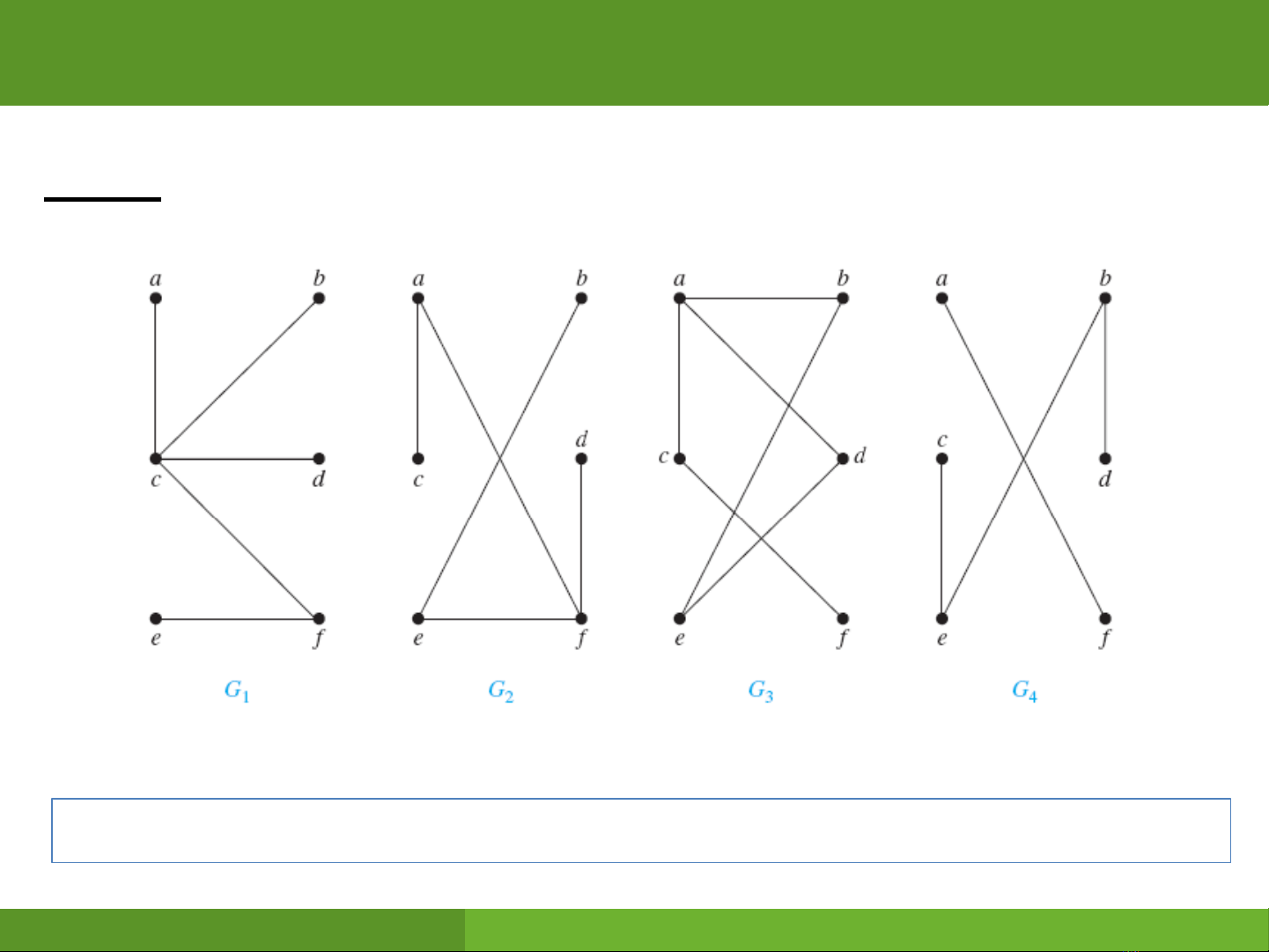
Ví dụ: Đồ thị nào sau đây là cây?
Đồ thị không có chu trình đơn và không liên thông gọi là rừng.
Nguyễn Quỳnh Diệp