1
TOÁN R I R C Ờ Ạ
NG D NG TRONG TIN H CỨ Ụ Ọ
Đ TH PH NG VÀ CÁC BÀI TOÁN Ồ Ị Ẳ
V TÔ MÀU Đ THỀ Ồ Ị
2
Ch ng 2. Đ th ph ng và bài toán tô màu đ thươ ồ ị ẳ ồ ị
Đ TH PH NGỒ Ị Ẳ
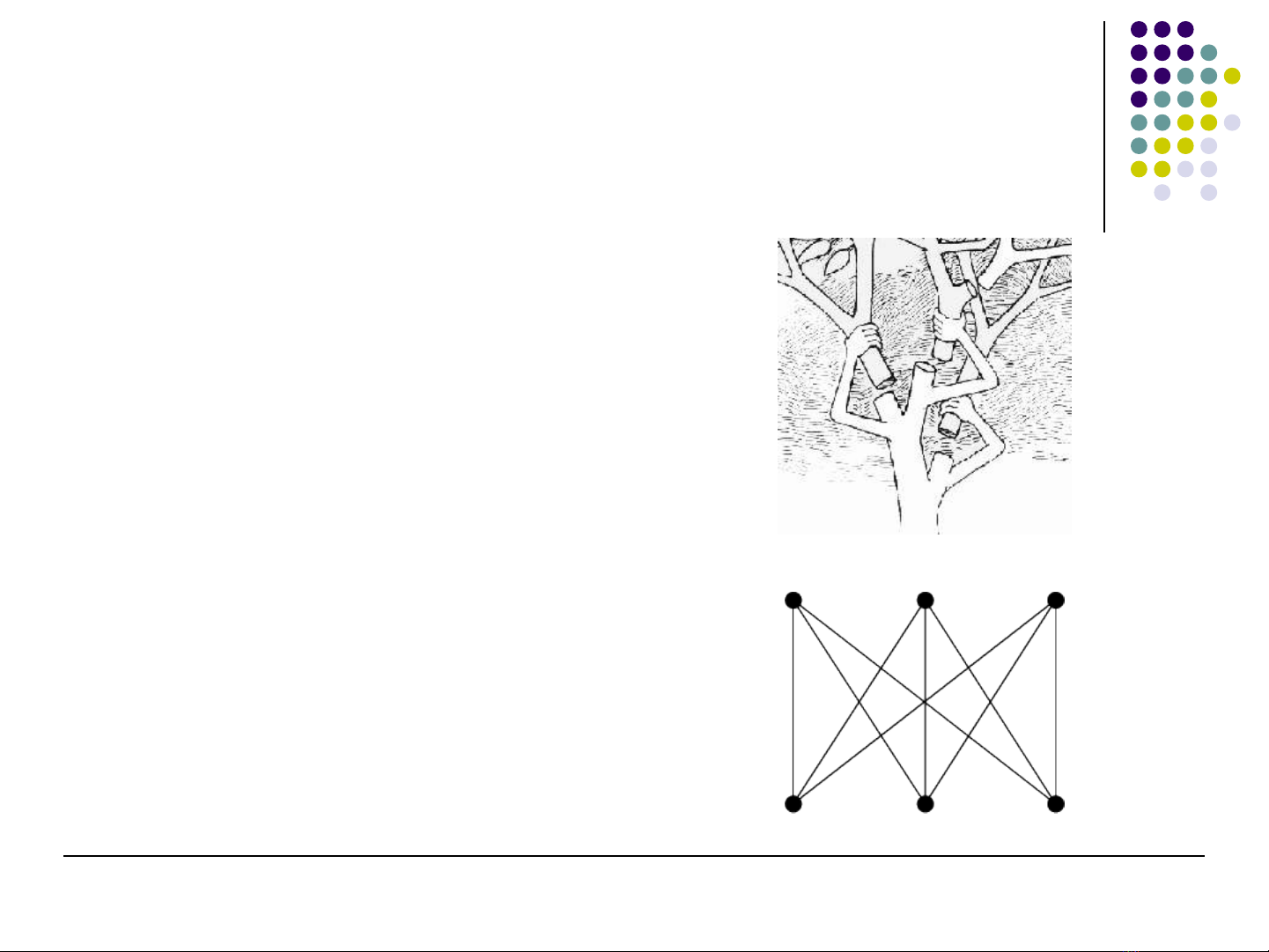
Bài toán
Tìm cách làm cho các con
đ ng đi d n t 3 ngôi nhà ườ ẫ ừ
t i 3 cái gi ng sao cho ớ ế
không có 2 con đ ng nào ườ
c t nhau?ắ
Mô hình bài toán
Đ nhỉ: các gia đình và
gi ng n cế ướ
C nhạ: đ ng đi t nhà ườ ừ
đ n các gi ngế ế
Có th v đ th mà không ể ẽ ồ ị
có 2 c nh nào c t nhau?ạ ắ
3
Ch ng 2. Đ th ph ng và bài toán tô màu đ thươ ồ ị ẳ ồ ị
Đ TH PH NGỒ Ị Ẳ
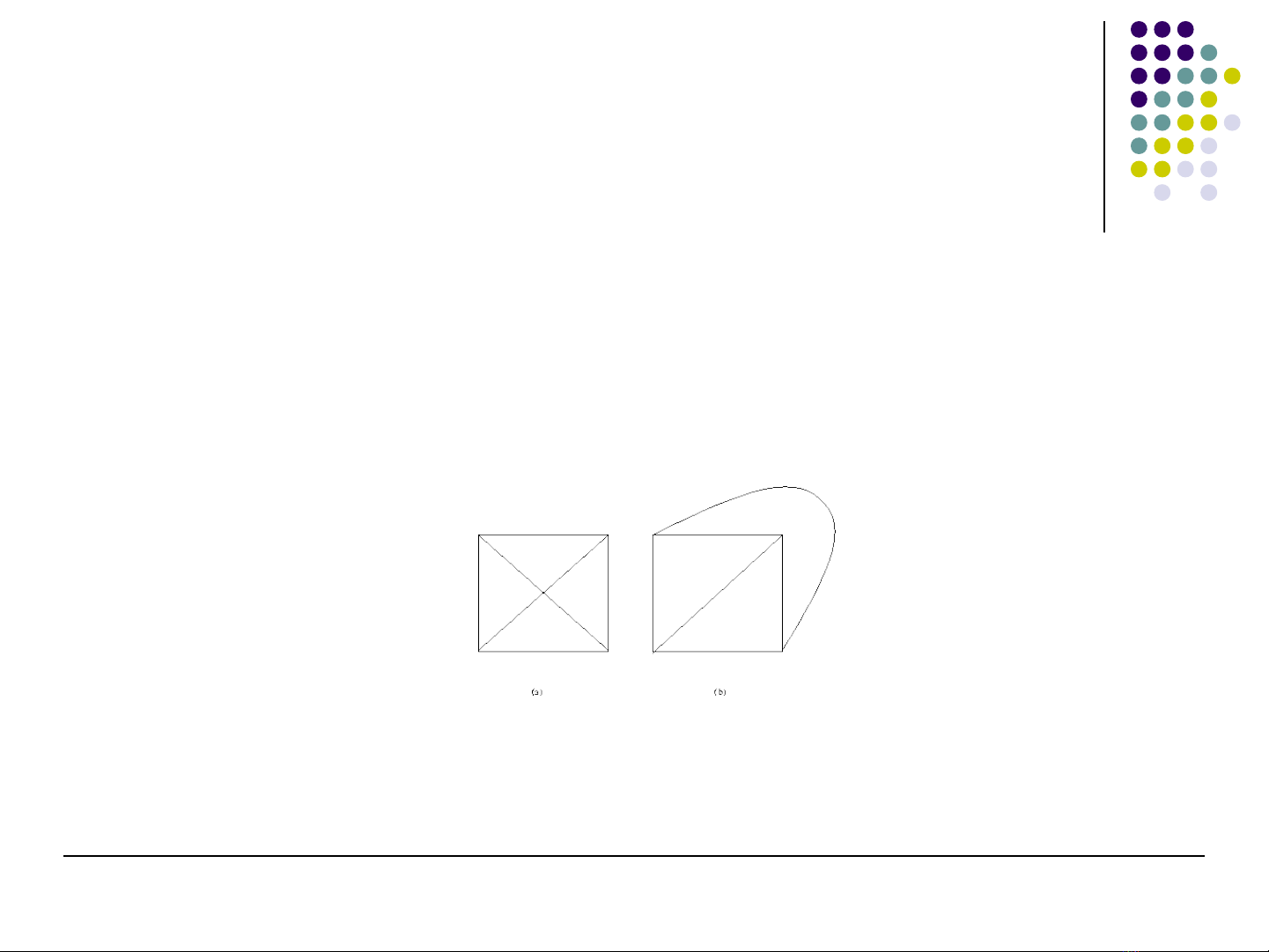
Đ th ph ngồ ị ẳ
M t đ th đ c g i là ph ng n u nó có th v ộ ồ ị ượ ọ ẳ ế ể ẽ
đ c trên m t m t ph ng mà không có các c nh ượ ộ ặ ẳ ạ
nào c t nhau đi m không ph i là đi m mút c a ắ ở ể ả ể ủ
m i c nh. ỗ ạ
Hình v nh v y đ c g i là m t bi u di n ẽ ư ậ ượ ọ ộ ể ễ
ph ng c a đ th .ẳ ủ ồ ị
4
Ch ng 2. Đ th ph ng và bài toán tô màu đ thươ ồ ị ẳ ồ ị
Đ TH PH NGỒ Ị Ẳ
Đ th ph ngồ ị ẳ
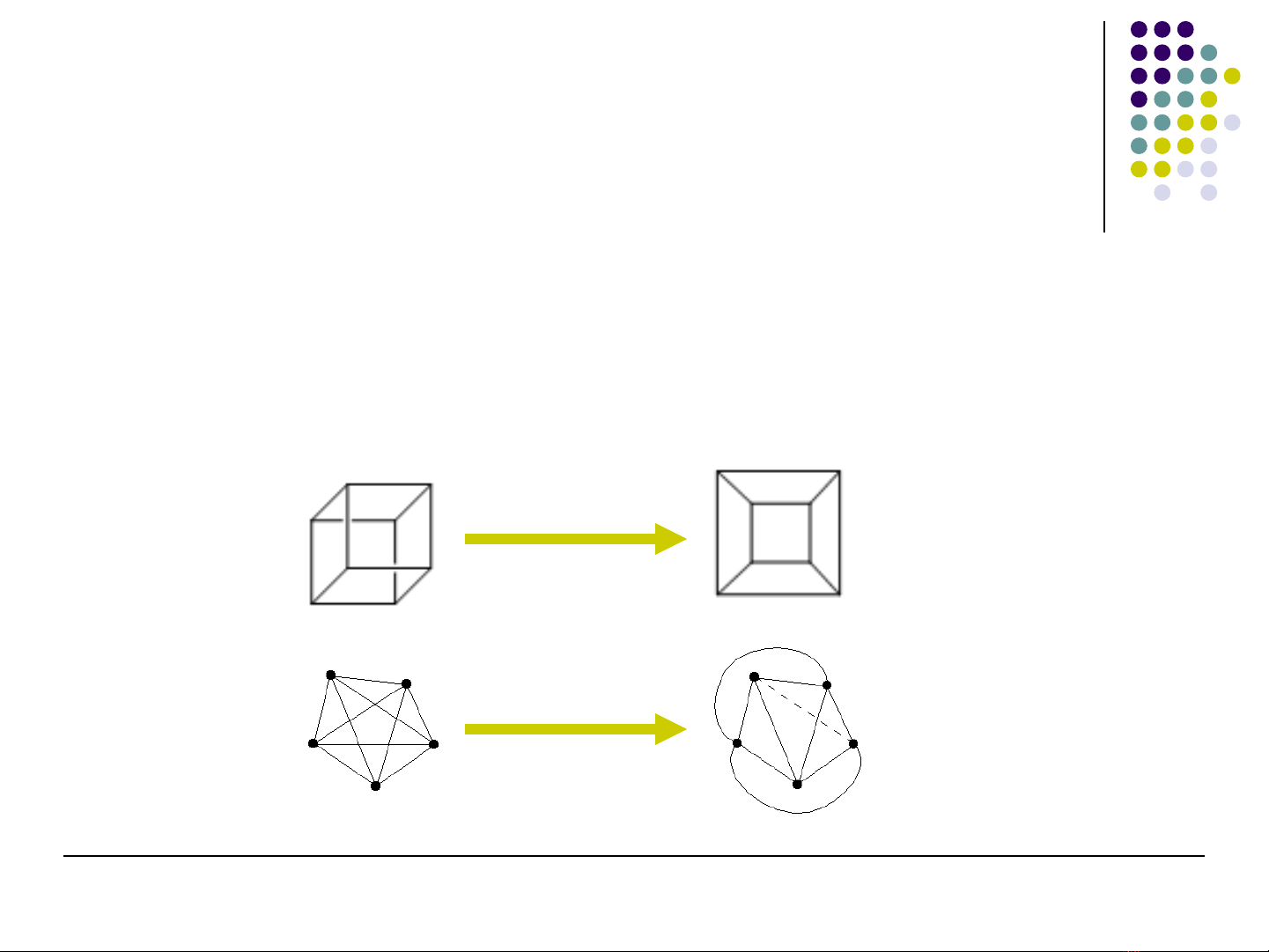
Ví dụ
Đ th sau có ph i là đ th ph ng không?ồ ị ả ồ ị ẳ
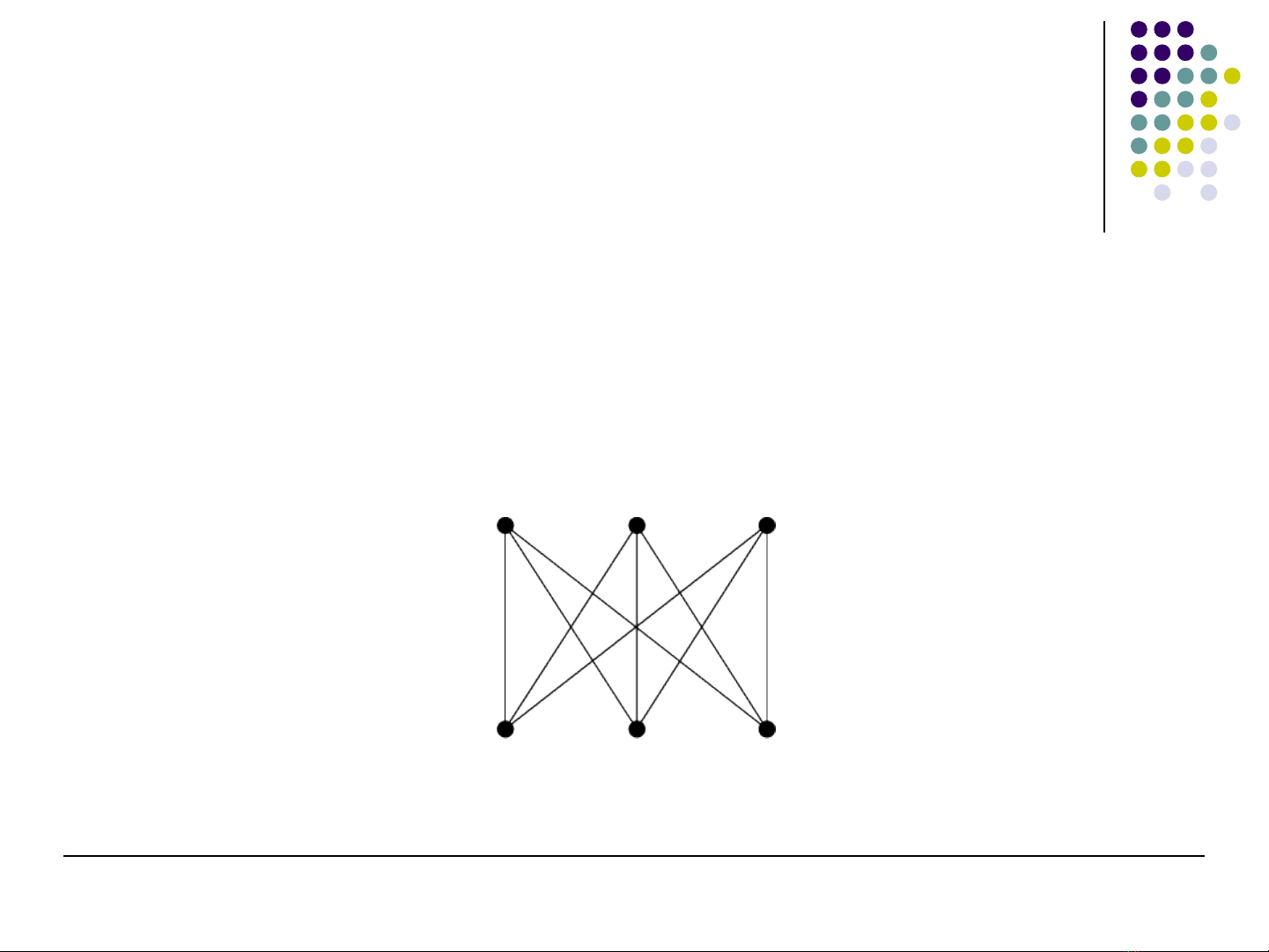
5
Ch ng 2. Đ th ph ng và bài toán tô màu đ thươ ồ ị ẳ ồ ị
Đ TH PH NGỒ Ị Ẳ
Đ th ph ngồ ị ẳ
Ví dụ
Đ th sau có ph i là đ th ph ng không?ồ ị ả ồ ị ẳ


















![Giáo trình Giải tích hàm một biến 1: Phần 2 [Full Nội Dung]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260127/hoatulip0906/135x160/60731769587731.jpg)
![Giáo trình Giải tích hàm một biến 1: Phần 1 [Full]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260127/hoatulip0906/135x160/70271769587732.jpg)



![Bài tập Toán cao cấp (HP1) [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260127/hoahongcam0906/135x160/69221769507713.jpg)


