1
TOÁN R I R C Ờ Ạ
NG D NG TRONG TIN H CỨ Ụ Ọ
KHÁI NI M C B N V CÂYỆ Ơ Ả Ề
2
Ch ng 2. Câyươ
M t s khái ni m c b nộ ố ệ ơ ả
Cây
Đ nh nghĩa: ị
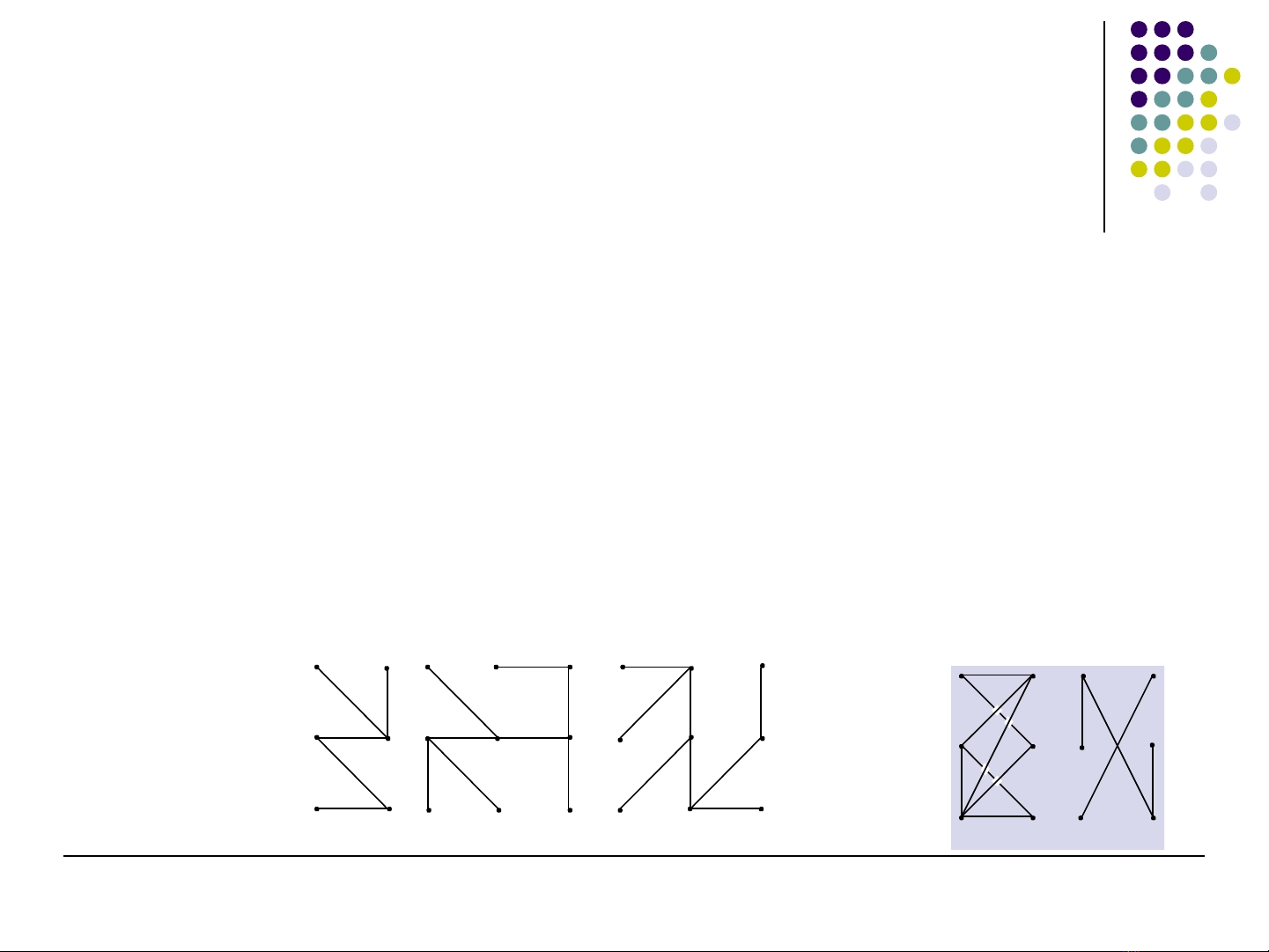
Cây là m t đ th ộ ồ ị vô h ngướ , liên thông và không có
chu trình s c pơ ấ
Cây không có c nh b i và khuyênạ ộ
Cây là m t đ n đ thộ ơ ồ ị
Ví dụ
G
1
G
2
G
G
3
G
4
3
Ch ng 2. Câyươ
M t s khái ni m c b nộ ố ệ ơ ả
R ngừ
Đ nh nghĩa: ị
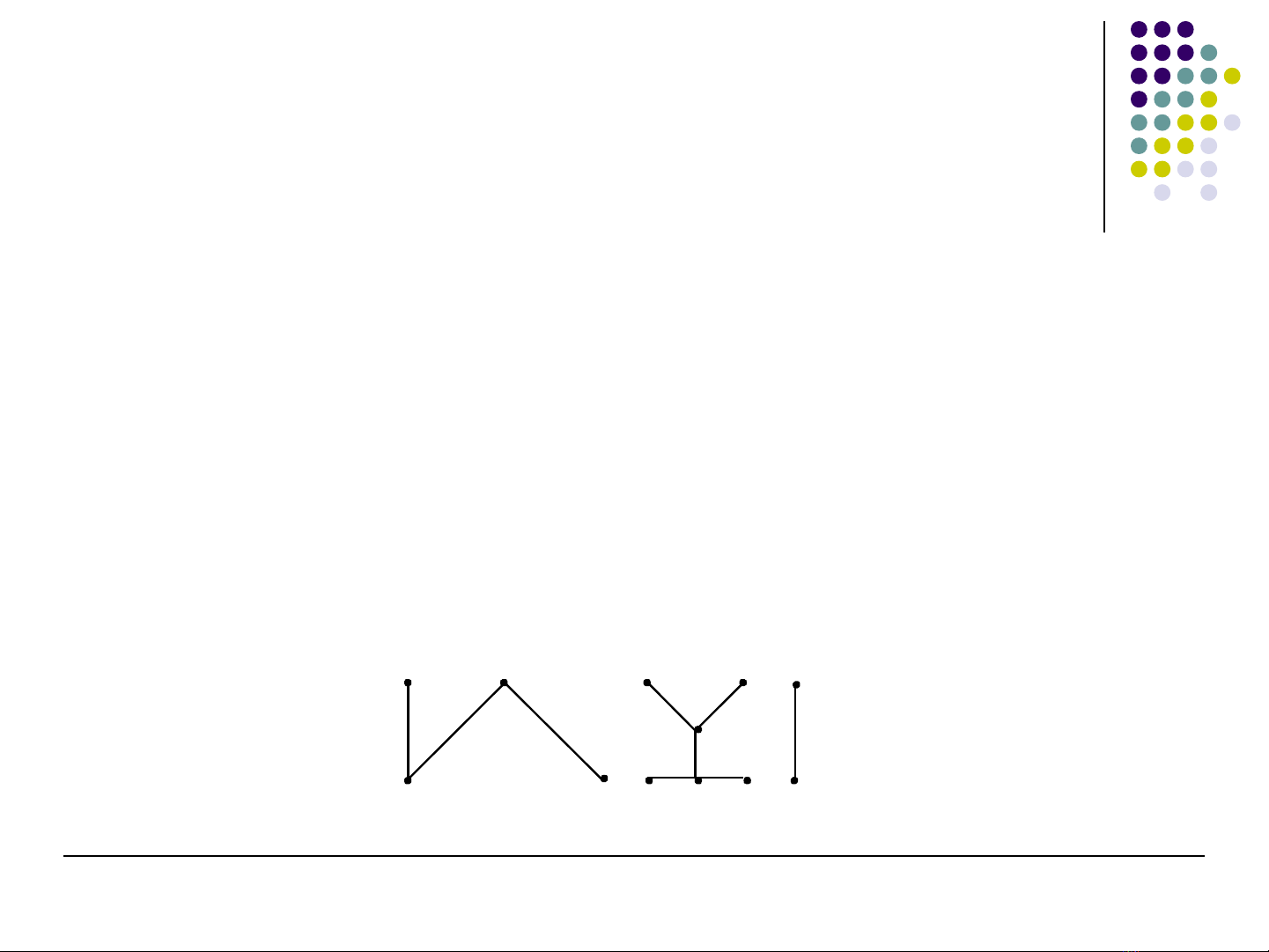
R ng là m t đ th ừ ộ ồ ị vô h ng ướ và không có chu trình
R ng có th có nhi u thành ph n liên thôngừ ể ề ầ
M i thành ph n liên thông là m t câyỗ ầ ộ
Ví dụ
G

4
Ch ng 2. Câyươ
M t s khái ni m c b nộ ố ệ ơ ả
Đ nh lý (Đi u ki n đ c a cây)ị ề ệ ủ ủ
N u m i c p đ nh c a m t đ th vô h ng G ế ọ ặ ỉ ủ ộ ồ ị ướ
luôn t n t i m t đ ng đi s c p thì G là m t câyồ ạ ộ ườ ơ ấ ộ
Ch ng minhứ
SV tham kh o tài li uả ệ
5
Ch ng 2. Câyươ
M t s khái ni m c b nộ ố ệ ơ ả
Cây có g cố
Đ nh nghĩaị
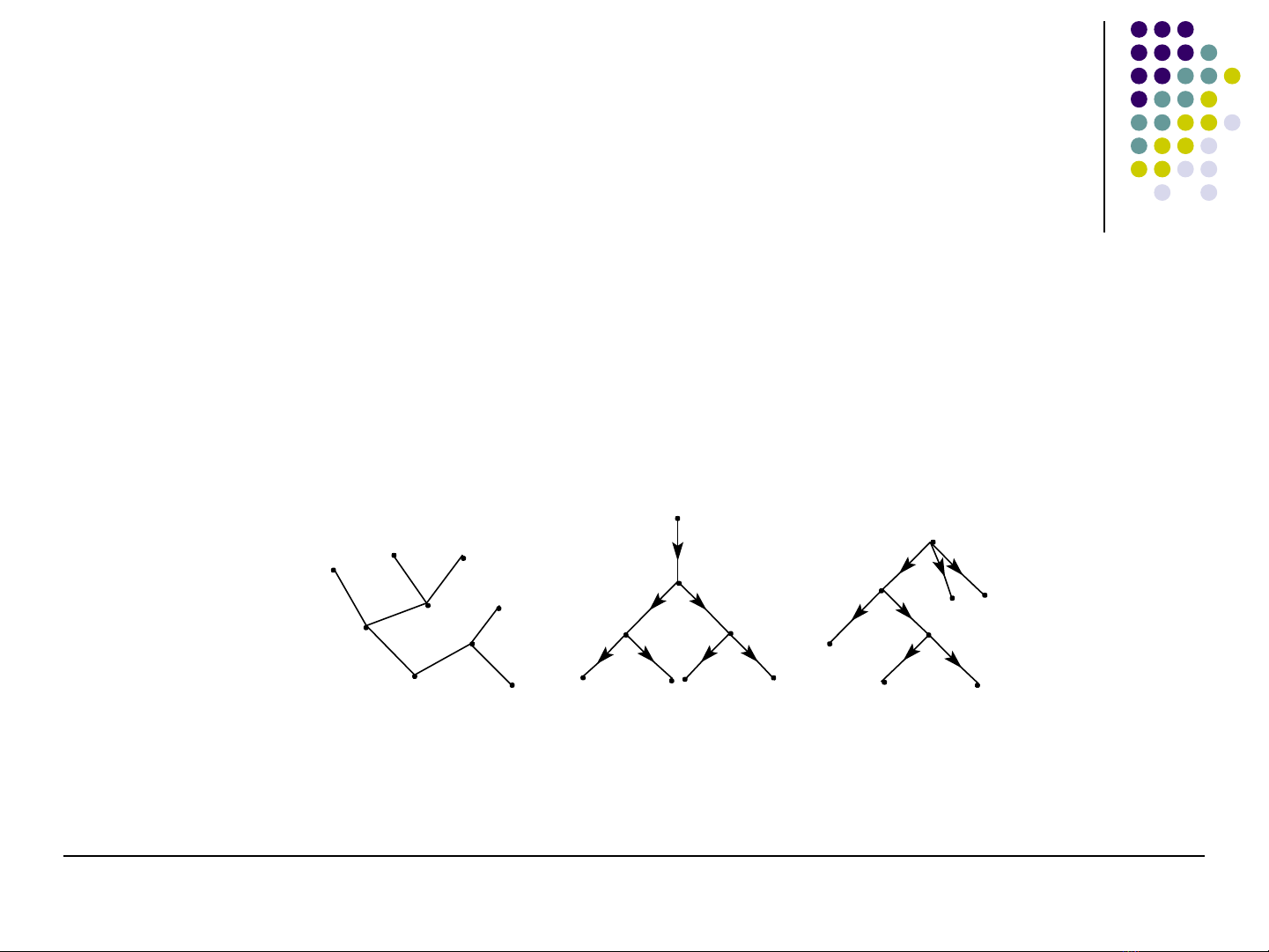
M t cây v i m t đ nh đ c ch n làm g cộ ớ ộ ỉ ượ ọ ố
Đ nh h ng các c nh trên cây t g c đi raị ướ ạ ừ ố
Ví dụ
Cùng m t cây, n u ch n g c khác nhau thì cây có g c thu ộ ế ọ ố ố
đ c s khác nhauượ ẽ
a
b
df
g
h
a
a
bb
c
cc
d
d
f
f
ggh h
ee
e


















![Giáo trình Giải tích hàm một biến 1: Phần 2 [Full Nội Dung]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260127/hoatulip0906/135x160/60731769587731.jpg)
![Giáo trình Giải tích hàm một biến 1: Phần 1 [Full]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260127/hoatulip0906/135x160/70271769587732.jpg)



![Bài tập Toán cao cấp (HP1) [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260127/hoahongcam0906/135x160/69221769507713.jpg)


