B MÔN TOÁN NG D NG - ĐHBKỘ Ứ Ụ
-------------------------------------------------------------------------------------
TOÁN 1 HK1 0708
•BÀI 4: VCBÉ – VCL N. LIÊN T C (SINH VIÊN)Ớ Ụ
•TS. NGUY N QU C LÂN (11/2007)Ễ Ố
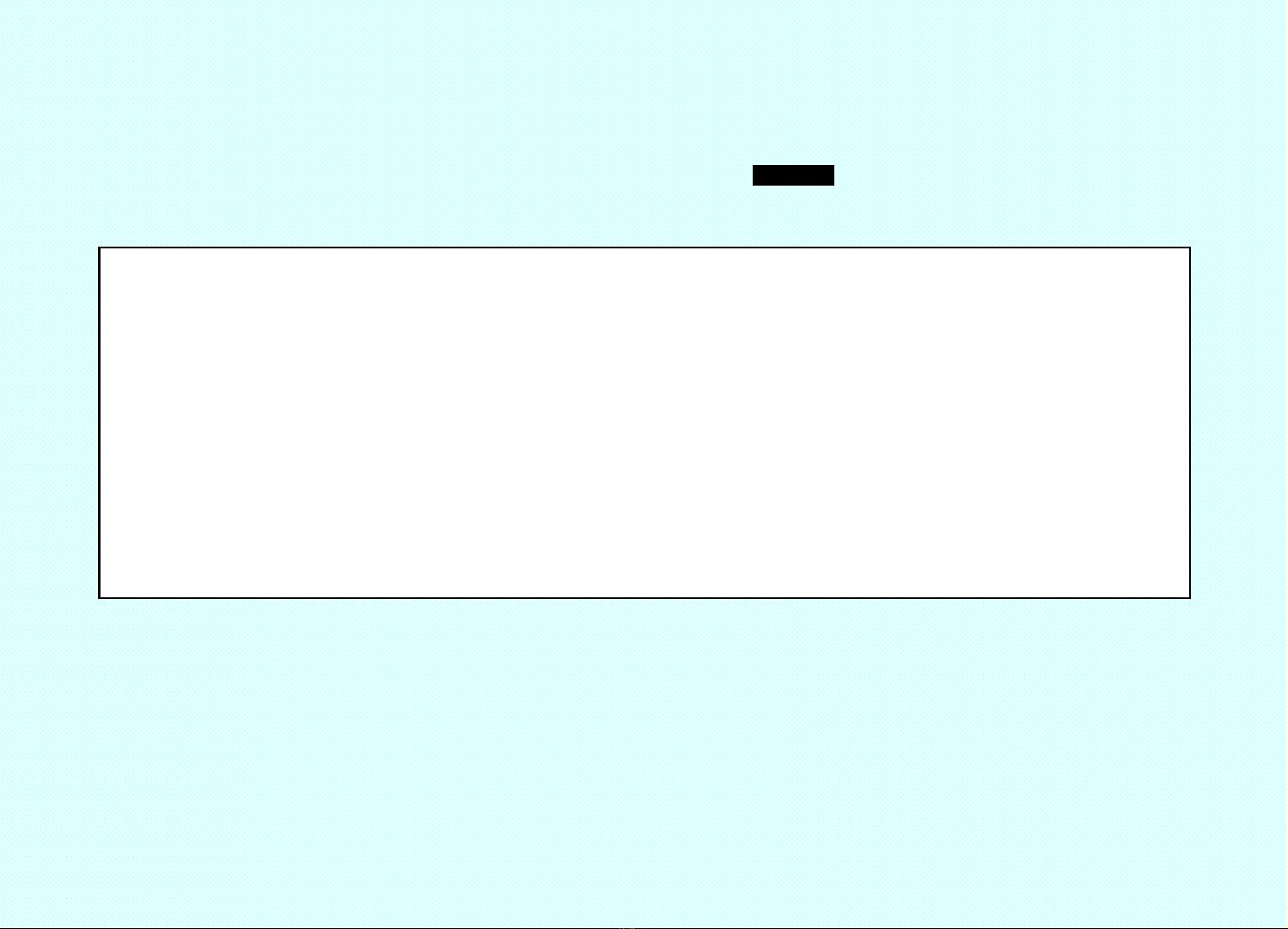
VÔ CÙNG BÉ
---------------------------------------------------------------------------------------------------------------------------------
0lim
0
x
xx
Đi lạ ư ng ợ(x) – vô cùng bé (VCB) khi x x0:
VCB cơ b n (ảx 0): Lưng giácợ
xxxx tg,cos1,sin
Mũ, ln:
xe
x
1ln,1
Lũy th a:ừ
131:VD.11 xx
x0: Không quan tr ng. VCB ọx :
x
1
VCB x 1: sin(x–1) …
VD:
x
xc
x
xb
x
a
xxx
sinlim/sinlim/sinlim/
00
(x), (x) – VCB khi x x0
(x) (x) , (x)(x): VCB C(x)(x): VCB
(x) VCB, C(x) b ch nị ặ
BT:
xx
x
sin1sinlim
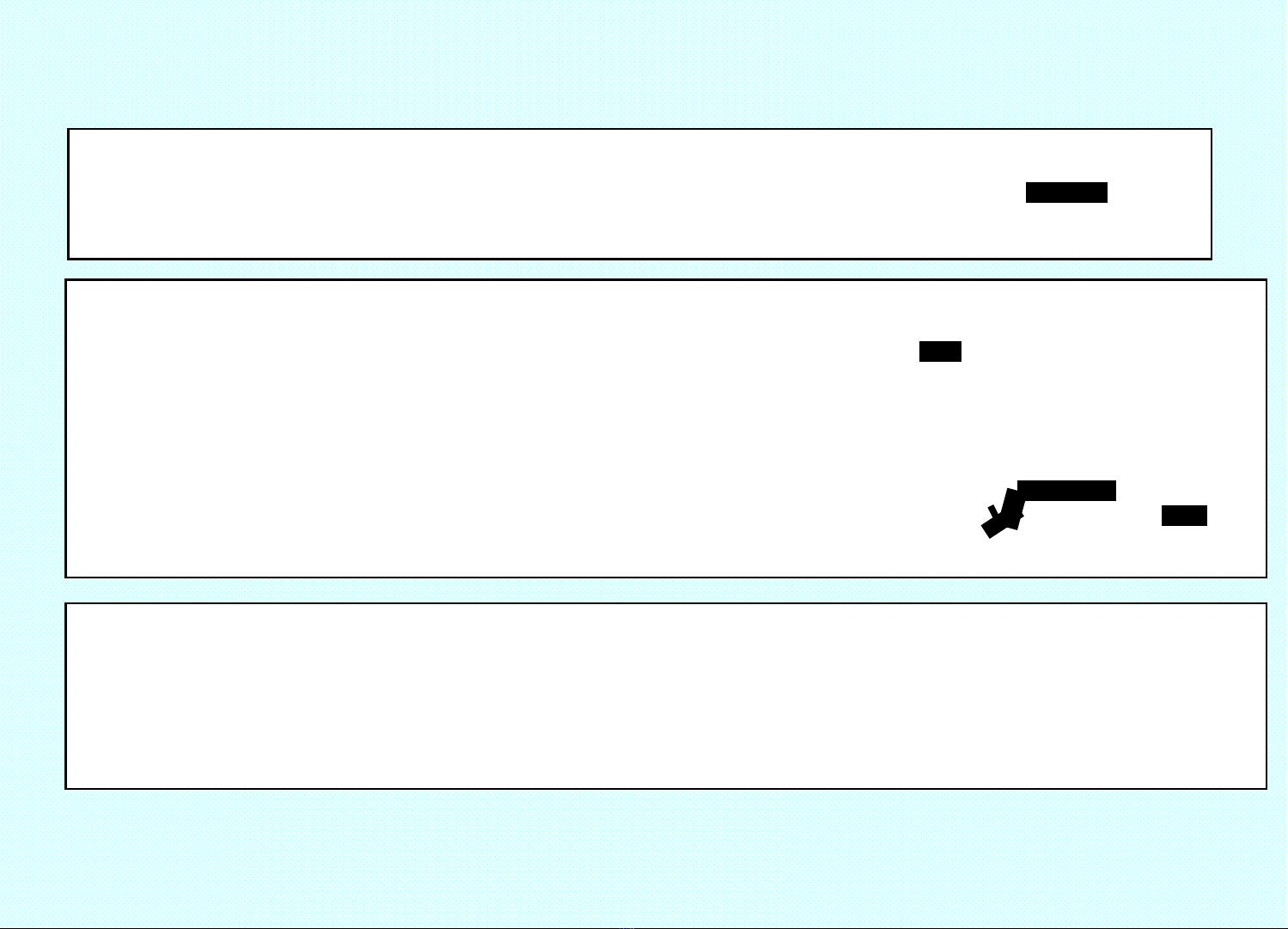
SO SÁNH VÔ CÙNG BÉ
--------------------------------------------------------------------------------------------------------------------------------
(x), (x) – VCB, x x0 và
c
x
x
xx
0
lim
So sánh đưcợ
VD: So sánh VCB:
xxx tg,cos1,sin
1/ c = 0 : (x) – VCB c p cao so v i ấ ớ (x): (x) = o((x))
2/ c = : Ngưc l i trợ ạ ư ng h p c = 0 ờ ợ (x) = o((x))
3/ c 0, c : vô cùng bé cùng c pấ
Cách nói khác: (x) – VCB c p th p hấ ấ ơn
VCB c p th p: Ch a ít “th a s 0” hấ ấ ứ ừ ố ơn. VD: sin2x, x3
Aùp d ng: So sánh 2 vô cùng bé ụxm , xn (m, n > 0) khi x 0
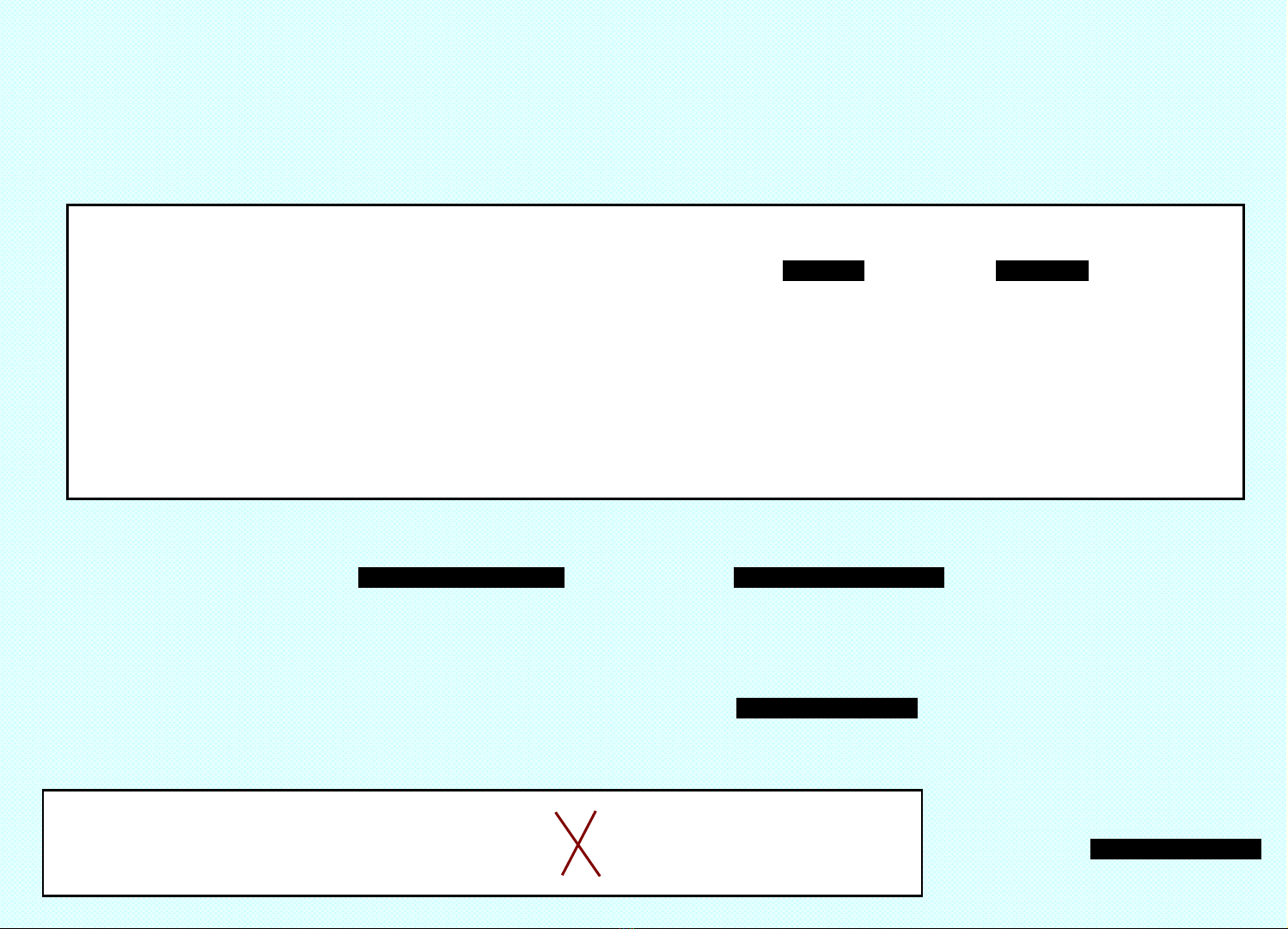
VÔ CÙNG BÉ TƯƠNG ĐƯƠNG – (QUAN TR NG) Ọ
-----------------------------------------------------------------------------------------------------------------------------------
(x), (x) – VCB tương đương khi x x0
1lim
0
x
x
xx
VD: Tìm h ng s C và ằ ố đ:ể
0,~sintg xCxxx
VCB tương đương: Đưc phép thay th a s tợ ừ ố ương đương vào
tích & thương (nhưng không thay vào t ng & hi u!) ổ ệ
VCB lưng giác:ợ
0,
2
~cos1,~tg,~sin
2
x
x
xxxxx
VCB mũ, ln:
0,~1ln,~1 xxxxe
x
VCB lũy th a (cừăn):
0,~11 xxx
VD:
3
2
~21
3
x
x
DÙNG VÔ CÙNG BÉ TÍNH GI I H N Ớ Ạ
-----------------------------------------------------------------------------------------------------------------------------------
3
0
tgsin
lim x
xx
x
:VD
~ & 1 ~ 1 khi x x0 1 ~ 1
VD: Tìm
xx
x
x
sin
tg21ln
lim
2
0
1/
xe
x
x
x
sin1
3cosln
lim/2
2
0
x có th ể x0 b t k . VD: Tìm ấ ỳ
x
x
xx
xx
1
32
lim
2
2
Aùp d ng: Dùng vô cùng bé tụ ương đương tính gi i ớ
h nạ
x
x
x
x
xx
xxxxxxxx 1
1
11
0000
limlim~,~
Tìm lim: Có th ểthay VCB tđương vào TÍCH (THƯƠNG)
Nhưng không thay tùy ti n VCB tệđương vào T NG (HI U)Ổ Ệ