BÀI GIẢNG 3: ÔN TẬP XÁC SUẤT THỐNG KÊ
ThS Phùng Thanh Bình
1
BÀI GIẢNG 3
MỘT SỐ VẤN ĐỀ CƠ BẢN
VỀ XÁC SUẤT THỐNG KÊ
TRONG KINH TẾ LƯỢNG
MỤC TIÊU BÀI GIẢNG:
1. Ký hiệu tổng
2. Phép thử, không gian mẫu và biến cố
3. Biến ngẫu nhiên
4. Xác suất
5. Biến ngẫu nhiên và hàm phân phối xác suất
6. Hàm mật độ xác suất đa biến
7. Đặc điểm của các phân phối xác suất
8. Một số phân phối xác suất quan trọng
9. Một số phép toán ma trận
10. Suy diễn thống kê
ĐỐI TƯỢNG BÀI GIẢNG:
1. Tài liệu bài giảng cho sinh viên đại học
2. Tài liệu tham khảo ôn tập cho học viên cao học
KÝ HIỆU TỔNG
Ký hiệu tổng
Ký tự (sigma) được thống nhất sử dụng để chỉ tổng:
n21
n
1i ii X...XXXX
(3.1)
Thao tác với Eviews
Trên cửa sổ lệnh của Eviews ta nhập: scalar sumX=@sum(x)
BÀI GIẢNG 3: ÔN TẬP XÁC SUẤT THỐNG KÊ
ThS Phùng Thanh Bình
2
Tính chất của phép toán tổng
1. Khi k là một hằng số
nkk
n
1i
(3.2)
2. Khi k là một hằng số
n
1i i
n
1i iXkkX
(3.3)
3. Tổng của tổng hai biến Xi và Yi
iiii YX)YX(
(3.4)
4. Tổng của một hàm tuyến tính
ii Xbna)bXa(
(3.5)
PHÉP THỬ, KHÔNG GIAN MẪU, VÀ BIẾN CỐ
Phép thử
Một phép thử có hai đặc tính:
1) Không biết chắc kết quả nào xảy ra
2) Nhưng biết được các kết quả có thể xảy ra
Không gian mẫu hay tổng thể
Tập hợp tất cả các kết quả có thể xảy ra của một phép thử
được gọi là tổng thể hay không gian mẫu.
Biến cố
Một biến cố là một nhóm các kết quả có thể xảy ra củ một
phép thử. Nói cách khác, đó là một tập hợp con của không
gian mẫu.
Các phép tính về biến cố:
Biến cố hội (AB): A xảy ra hay B xảy ra
Biến cố giao (AB): A xảy ra vả B xảy ra
Biến cố phụ (
A
):
A
xảy ra, A không xảy ra
Biến cố xung khắc: AB =
BÀI GIẢNG 3: ÔN TẬP XÁC SUẤT THỐNG KÊ
ThS Phùng Thanh Bình
3
BIẾN NGẪU NHIÊN
Ví dụ, tung hai đồng xu, quan sát và lập thành bảng kết
quả của các phép thử như sau:
BẢNG 3.1: Định nghĩa khái niệm biến ngẫu nhiên
Nguồn: Gujarati, 2006, trang 25
Ta gọi biến “số mặt ngửa” là một biến ngẫu nhiên. Nói một
cách tổng quát, một biến mà giá trị (bằng số) của nó được
xác định bởi kết quả của một phép thử được gọi là một
biến ngẫu nhiên. Như vậy, biến ngẫu nhiên là biến mà giá
trị của nó được xác định một cách ngẫu nhiên.
Một biến ngẫu nhiên có thể có giá trị rời rạc hoặc
liên tục. Một biến ngẫu nhiên rời rạc chỉ có một số giá
trị hữu hạn (hoặc vô hạn có thể đếm được). Một biến ngẫu
nhiên liên tục là một biến ngẫu nhiên có bất kỳ giá trị
nào trong một khoảng giá trị nào đó.
XÁC SUẤT
Xác suất của một biến cố: Định nghĩa cổ điển
Nếu một phép thử có thể có n kết quả loại trừ nhau và có
khả năng xảy ra như nhau, và nếu m kết quả từ phép thử
này hợp thành biến cố A, thì P(A), xác suất để A xảy ra,
là tỷ số m/n.
n
m
)A(P
(3.6)
Xác suất của một biến cố: Tần suất tương đối
Để giới thiệu khái niệm này, ta xem ví dụ sau đây. Dữ
liệu trong bảng 3.1 là phân phối điểm điểm thi mô kinh tế
vi mô của 200 sinh viên. Đây là một ví dụ về phân phối
BÀI GIẢNG 3: ÔN TẬP XÁC SUẤT THỐNG KÊ
ThS Phùng Thanh Bình
4
tần suất cho biết các điểm ngẫu nhiên được phân phối như
thế nào. Các con số trong cột 3 là các tần suất tuyệt
đối, nghĩa là số lần xảy ra của một biến cố nhất định.
Các con số trong cột 4 được gọi là các tần suất tương
đối, nghĩa là số tần suất tuyệt đối chia tổng số lần xảy
ra.
BẢNG 3.2: Phân phối điểm KTL của 200 sinh viên
Điểm
Điểm giữa của
khoảng
Tần suất
tuyệt đối
Tần suất tương
đối
0-9
10-19
20-29
30-39
40-49
50-59
60-69
70-79
80-89
90-99
5
15
25
35
45
55
65
75
85
95
0
0
0
10
20
35
50
45
30
10
Tổng 200
0
0
0
0.050
0.100
0.175
0.250
0.225
0.150
0.050
1.000
Nguồn: Gujarati, 2006, trang 28
PHÂN PHỐI XÁC SUẤT
Phân phối xác suất của một biến ngẫu nhiên rời rạc
Giả sử X là một biến ngẫu nhiên rời rạc với các giá trị
x1, x2, ... thì hàm f được xác định bởi
f(X=xi) = P(X=xi) i = 1, 2, … (3.7)
=0 nếu x ≠ xi
được gọi là hàm phân phối xác suất của biến ngẫu nhiên X,
ký hiệu là PMF hay PF, trong đó, P(X=xi) là xác suất X có
giá trị xi. Hàm PMF có các tính chất sau:
0 f(xi) 1 (3.8)
n
1i i1)x(f
(3.9)
Ví dụ, biến X là số mặt ngửa khi tung hai đồng xu, ta xét
bảng sau đây:
BÀI GIẢNG 3: ÔN TẬP XÁC SUẤT THỐNG KÊ
ThS Phùng Thanh Bình
5
0.25
0.5
0.25
0 1 2
Hình 3.1: PMF của biến ngẫu nhiên rời rạc
BẢNG 3.3: PMF của biến ngẫu nhiên rời rạc
Nguồn: Gujarati, 2006, trang 34
Phân phối xác suất của biến ngẫu nhiên liên tục
Ví dụ, gọi X là biến chiều cao của một người, được đo
bằng mét. Giả sử ta muốn tính xác suất để chiều cao của
một người trong khoảng 1.56m đến 1.80m.
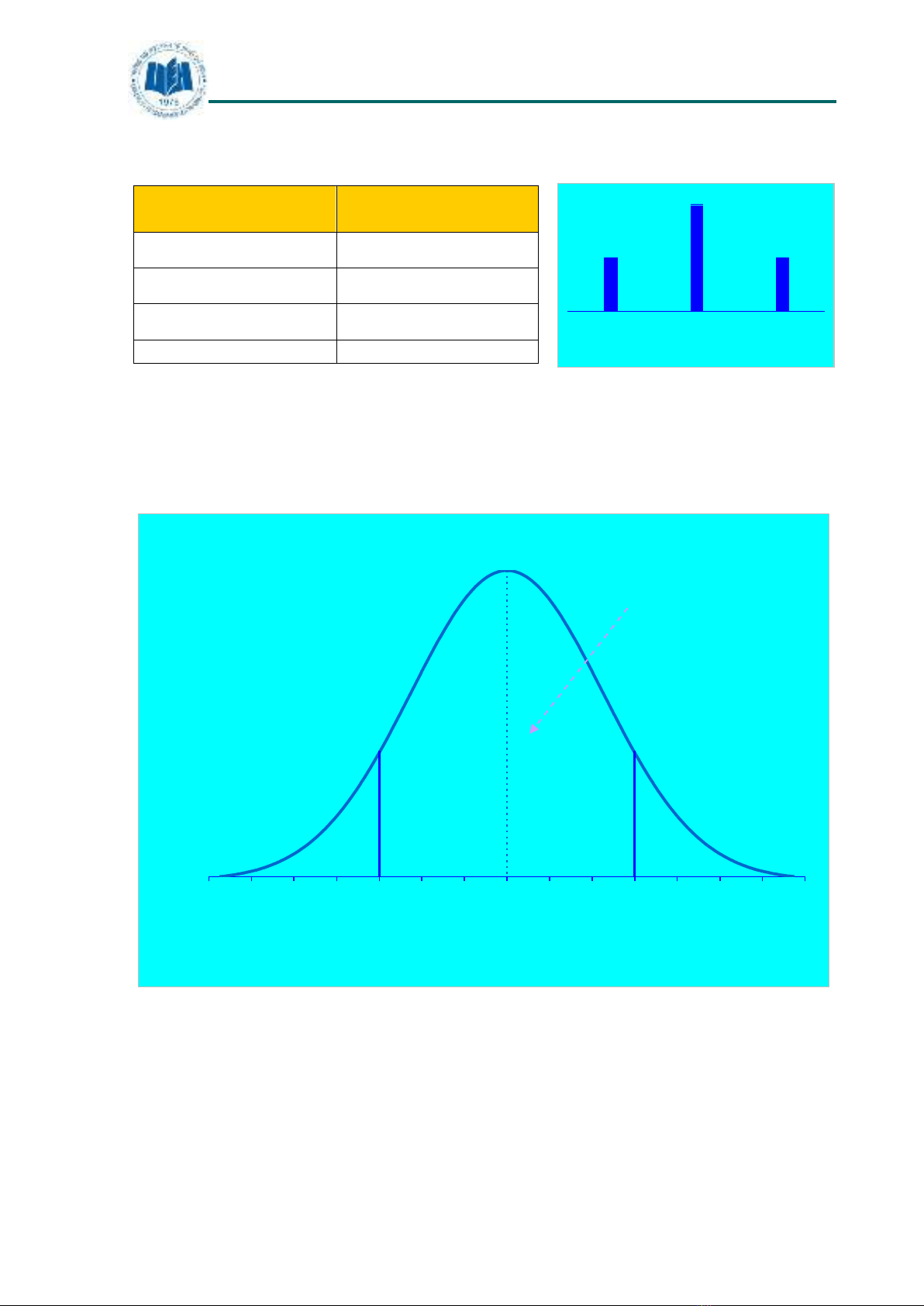
Hình 3.2: PDF của một biến ngẫu nhiên liên tục
0.04924276
0.54924276
1.04924276
1.54924276
2.04924276
2.54924276
3.04924276
3.54924276
4.04924276
1.4 1.44 1.48 1.52 1.56 1.6 1.64 1.68 1.72 1.76 1.8 1.84 1.88 1.92 1.96
Xác suất để chiều cao của một cá nhân nằm trong khoảng từ
1.56m đến 1.80m là diện tích dưới dường phân phối giữa
hai giá trị 1.56 và 1.80. Đối với một biến ngẫu nhiên
liên tục X, thì hàm mật độ xác suất f(X) như sau:
P(x1 X x2) =
2
1
x
x
dx)x(f
(3.10)
Hàm mật độ xác suất của một biến ngẫu nhiên X có các tính
chất sau đây:
Số mặt ngửa
X
PMF
f(X)
0
¼
1
½
2
¼
Tổng
1.00
Xác suất để chiều cao trong
khoảng 1.56 đến 1.8