HUST Khoa Toán - Tin
Đại học Bách khoa Hà Nội
Khoa Toán - Tin
BÀI TẬP GIẢI TÍCH I
MÃ HỌC PHẦN: MI1016
1.1-1.3. Hàm số. Hàm số sơ cấp cơ bản
1. Tìm tập xác định của các hàm số sau.
a) y=x
√4x2−1.
b) y= arcsin x
x+ 2.
c) y= ln 1−x
1 + x.
d) y=√arctan x.
2. Tìm tập giá trị của các hàm số sau.
a) y= ln(1 −2 sin x).
b) y= arctan (2ex).
c) y=√arccos x.
d) y=x2−1
x2+ 1.
3. Khi không khí khô di chuyển lên trên cao, nó nở ra và nguội đi. Nhiệt độ ở mặt đất là
30◦Cvà nhiệt độ ở độ cao 1 km là 20◦C.
a) Biểu thị nhiệt độ T(theo ◦C) dưới dạng hàm số của độ cao h(theo kilômét), giả
sử rằng mô hình tuyến tính là phù hợp.
b) Vẽ đồ thị hàm số T(h).
c) Nhiệt độ ở độ cao 4 km là bao nhiêu?
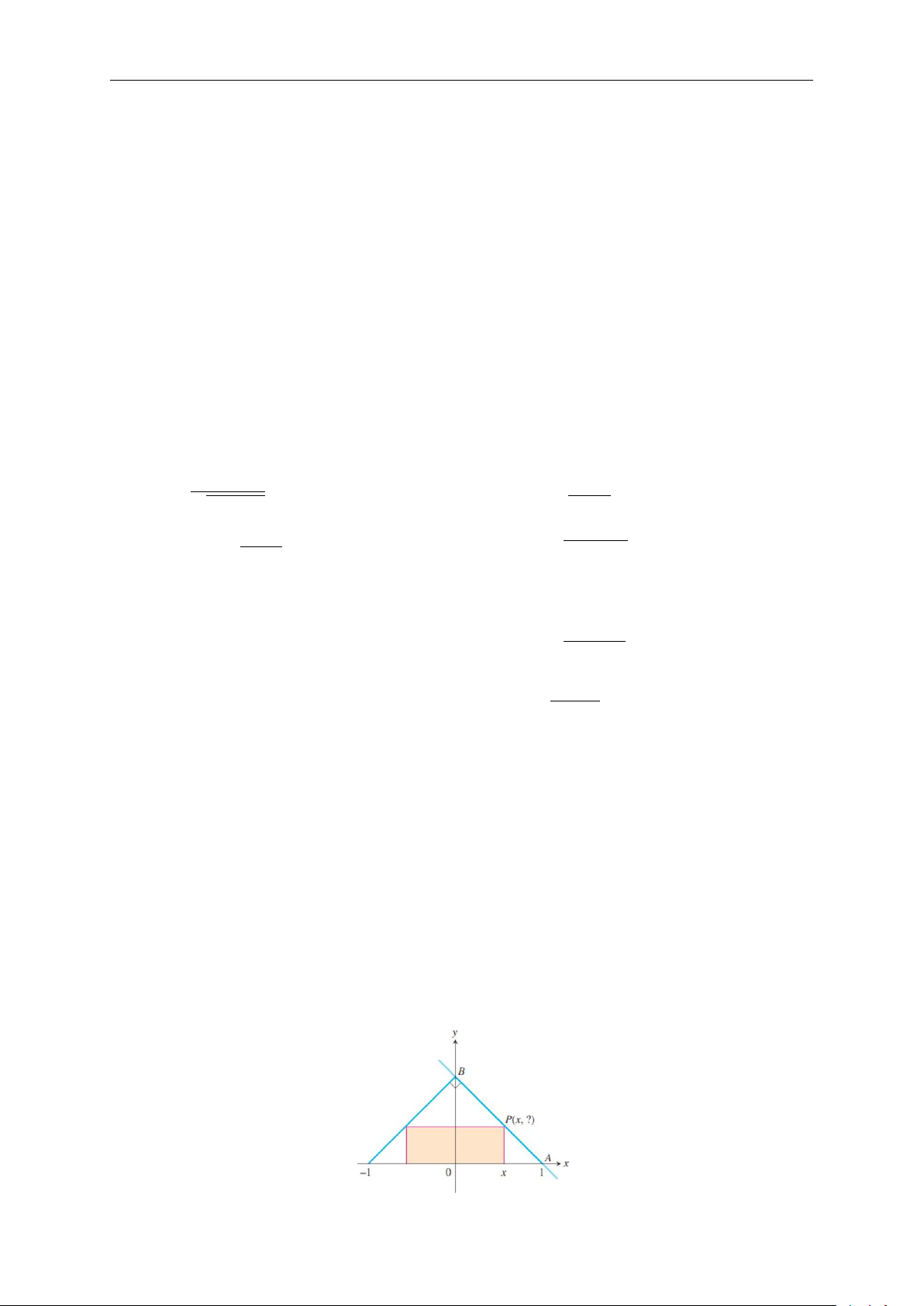
4. Xét một hình chữ nhật nội tiếp trong một tam giác vuông cân có cạnh huyền dài 2
đơn vị như hình minh họa dưới đây.
1
HUST Khoa Toán - Tin
a) Biểu thị tọa độ ycủa Ptheo x.
b) Biểu thị diện tích hình chữ nhật theo x.
5. Xét tính chẵn, lẻ của hàm số f.
a) f(x) = ex−e−x
2=: sinh x.
b) f(x) = 2x−x2
2x+x2.
c) f(x) = ln x+√x2+ 1.
d) f(x) = ln 1−x
1 + x.
e) f(x) = sin x+ cos 2x.
f) f(x) = sin x+ sin 2x.
6. Tìm các hàm số hợp f◦g, g ◦f, f ◦f,g◦gvà tập xác định của chúng.
a) f(x) = 1
x+ 1,g(x) = x−1.
b) f(x) = √2x+ 3,g(x) = x2+ 1.
c) f(x) = sin x,g(x) = √x+ 1.
d) f(x) = 1 −x2,g(x) = 1−x
1 + x.
7. Tìm hàm ngược của các hàm số sau.
a) y= arcsin 2x.
b) y=e2x−e−2x
2.
c) y=1−3x
1+3x.
d) y= ln ex−1
ex+ 1.
2
HUST Khoa Toán - Tin
2.1 - 2.3. Giới hạn
8. Tìm giới hạn của các dãy số sau (nếu tồn tại)
a) un=3
√n3+ 2n2−n.
b) un= tan 2nπ
1+8n.
c) un= cos nπ
2.
d) un=n
n2+ 1 +n
n2+ 2 +··· +n
n2+n.
e) un=1−1
2nn
.
f) un=ncos (n2+ 1)
n2+ 2 .
9. Tìm giới hạn của dãy số {√2,p2 + √2,q2 + p2 + √2, . . .}.
10. Xác định vô cùng lớn αkhi x→ ∞ và số nguyên n(nếu tồn tại) sao cho αvà xn
cùng bậc.
a) α(x) = x3+ 2x2+x5.
b) α(x)=3x4+ sin x.
c) α(x) = sin(x2).
d) α(x) = ex+x2.
11. Xác định vô cùng bé αkhi x→0và số nguyên n(nếu tồn tại) sao cho αvà xncùng
bậc
a) α(x) = x3+ 2x2+x5.
b) α(x)=3x4+ sin x.
c) α(x) = sin(x2).
d) α(x) = ex+x2.
12. So sánh các cặp vô cùng bé sau khi x→0.
a) α(x) = sin(x2+x), β(x) = 1 −cos x.
b) α(x) = √x3+ 2x4, β(x) = ln(1 + 2x),
x→0+.
c) α(x) = esin x−1, β(x) = arcsin(tan x).
d) α(x) = tan(−x2+ 3x3), β(x) = sinh(3x2).
13. Tìm giới hạn.
a) lim
x→1
√x2+ 8 −3
x−1.
b) lim
x→0
tan x−sin x
x3.
c) lim
x→0
9x−5x
4x−3x.
d) lim
x→1
x6−1
x10 −1.
e) lim
x→0
ln (1 + 2x2)
1−cos x.
3
HUST Khoa Toán - Tin
f) lim
x→∞ x+ 1
x+ 32x
.
g) lim
x→∞ sin 1
x+ cos 1
xx
.
h) lim
x→0
ln(1 + 3 tan x)
ex−cos x.
i) lim
x→0+
√x5
√sin xln (1 −3x2).
j) lim
x→0
cos(sin x)−1
sin(cos x−1).
14. Giả sử lim
x→1
f(x)−8
x−1= 9, tính lim
x→1f(x).
3.1 - 3.6. Hàm số liên tục
15. Tìm ađể f(x) =
cx2+ 2,nếu x < 1
2ax3+ 1,nếu x≥1
liên tục tại mọi điểm x?
16. Chứng minh rằng hàm fliên tục trên (−∞,∞).
a) f(x) =
sin xnếu x < π
4
cos xnếu x≥π
4
.b) f(x) =
x2nếu x < 1
√xnếu x≥1
.
17. Xác định điểm gián đoạn của hàm số và minh họa bằng đồ thị
a) y=1
1 + e1/x .b) y= ln (tan2x).c) y=sin x
2x−1.
18. Tìm những điểm mà tại đó fkhông liên tục. Tại điểm nào trong những điểm này, f
liên tục phải, liên tục trái hoặc không liên tục?
a) f(x) =
2x−1
xif x < 0
2x+cif x≥0
.b) f(x) =
sin2(πx)
ln (1 + 2x2)if x < 1
√xif x≥1
.
19. Chứng minh rằng phương trình có nghiệm trong khoảng đã cho.
a) x6−3x+ 1 = 0,(0,1). b) x3=√3x+ 1,(1,2).
20. Một chuyến tàu khởi hành lúc 8 giờ sáng từ Hà Nội đến Hải Phòng, đến nơi lúc 11 giờ
sáng. Ngày hôm sau, tàu khởi hành lúc 8 giờ sáng từ Hải Phòng đến Hà Nội, đến nơi lúc
11 giờ sáng. Có điểm nào trên tuyến đường mà tàu sẽ đi qua cùng một thời điểm trong
ngày ở cả hai ngày không?
21. Cho hàm số fliên tục trên đoạn đóng [0,1] và f(0) = 1, f(1) = 0. Chứng minh rằng
tồn tại một số c∈(0,1) thoả mãn f(c) = c.
4
HUST Khoa Toán - Tin
4.1 - 4.6. Đạo hàm
22. Tính đạo hàm của các hàm số sau:
a) y= (x2+ 1) 3
√x2+ 2.
b) y= sin(tan x).
c) y=px+√x.
d) y= ln x+√x2+ 5.
e) y= sinnxcos nx.
f) y=1 + 1
xx
.
23. Với giá trị nào của avà bthì hàm số
f(x) =
ax nếu x < 2
ax2+bx + 3 nếu x≥2
khả vi với mọi x? Thảo luận về đồ thị của fkhi đó.
24. Cho f(x) =
x2nếu x≤2
mx +bnếu x > 2
. Tìm giá trị của mvà bsao cho fkhả vi tại mọi
điểm.
25. Cho r(x) = f(g(h(x))), với h(1) = 2, g(2) = 3, h0(1) = 4, g0(2) = 5, và f0(3) = 6. Tính
r0(1).
26. Nếu F(x) = f(3f(4f(x))), trong đó f(0) = 0 và f0(0) = 2, tính F0(0).
27. Đạo hàm của hàm số
h(x) =
x2sin(1/x)if x6= 0
0if x= 0
có liên tục tại x= 0 không? Câu hỏi tương tự với hàm k(x) = xh(x)? Giải thích.
28. Tìm y0(x)biết ylà một hàm của xđược xác định bởi phương trình
a) arctan(2x+y) = y3.
b) x3+y3= 3x2y.
c) cos(x−y) = xey.
29. Viết phương trình tiếp tuyến của đường cong 2x3+ 4y2= 6 tại điểm (1,1).
30. Tính x0(y)biết xlà hàm của yđược xác định bởi phương trình y2+ 2x3y+x= 0.
Từ đó viết phương trình tiếp tuyến của đường cong y2+ 2x3y+x= 0 tại điểm (1,−1).
5