Bài t p ph n UD hình h c c a tích phân képậ ầ ọ ủ
Tính di n tích mi n D gi i h n b iệ ề ớ ạ ở
1. x=y2-2y, x+y=0
2. y2=10x+25, y2=-6x+9
3. y=lnx, x=y+1, y=-1
4. y=4x-x2, y=2x2-5x
5. y2=4-4x, x2+y2=4 (phía ngoài parabol)
Gi i: ả
Nh c l i công th c ắ ạ ứ ( )
D
S D dxdy=��
Bài t p ph n UD hình h c c a tích phân képậ ầ ọ ủ
1. Ta tìm c n tích phân theo dyậ b ng cách ằkh xử t 2 ừ
ph ng trình 2 m tươ ặ
x=y2-2y=-y (1) ↔ y2-y=0 ↔ y=0, y=1
T đó suy ra ừ0≤y≤1, ta l y ng c l i ph ng trình 1 ấ ượ ạ ươ
đ đ c ti p c n đ i v i tích phân theo dxể ượ ế ậ ố ớ
y2-2y ≤x ≤ -y
V y : ậ
2
1
02
( 1)
y
y y
S D dy dx
-
-
=� �
1
2
0
1
( ) 6
y y dy= - =
￲
Bài t p ph n UD hình h c c a tích phân képậ ầ ọ ủ
2. Kh x t 2 ph ng trình đã choử ừ ươ
2 2
1 1
( 25) (9 ) (1) 15
10 6
y y y- = - =� �
Suy ra c n tích phân theo dy, t ng t nh trên, ta ậ ươ ự ư
thay vào ph ng trình (1) đ có c n tích phân theo dxươ ể ậ
V y : ậ
2
2
1(9 )
15 15
6
2
1
15 15
( 25)
10
1 16 15
( 2) (120 8 )
30 3
y
y
S D dy dx y dy
-
- -
-
= = - =
� � �
Bài t p ph n UD hình h c c a tích phân képậ ầ ọ ủ
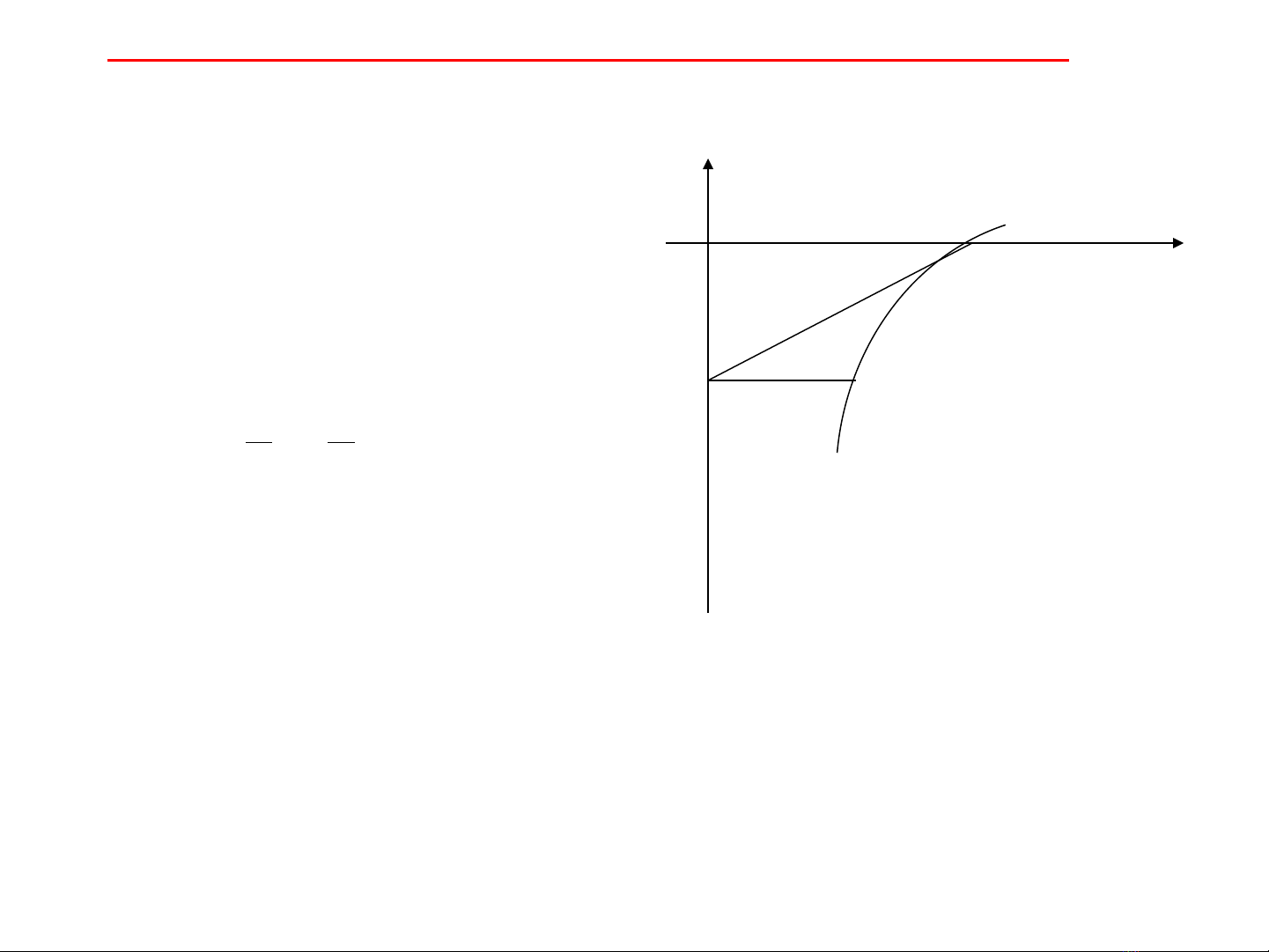
3. Ta s v mi n Dẽ ẽ ề 3 đ xác đ nh c n tích phân ể ị ậ
1
-1
y=lnx
0
3
1 1
( )
y
e
y
S D dy dx
- +
=� �
4. Tìm giao đi m 2 đ ng gi i h n Dể ườ ớ ạ
4x-x2=2x2-5x ↔ 0=3x2-9x ↔ x=0, x=3
Suy ra : 0≤x ≤3 ↔ 0 ≤3x2-9x ↔ 4x-x2 ≤2x2-5x
2
2
3 2 5
4
04
( )
x x
x x
S D dx dy
-
-
=� �
3
1 1
( ) 2
S D e
= -
=27/2
Bài t p ph n UD hình h c c a tích phân képậ ầ ọ ủ
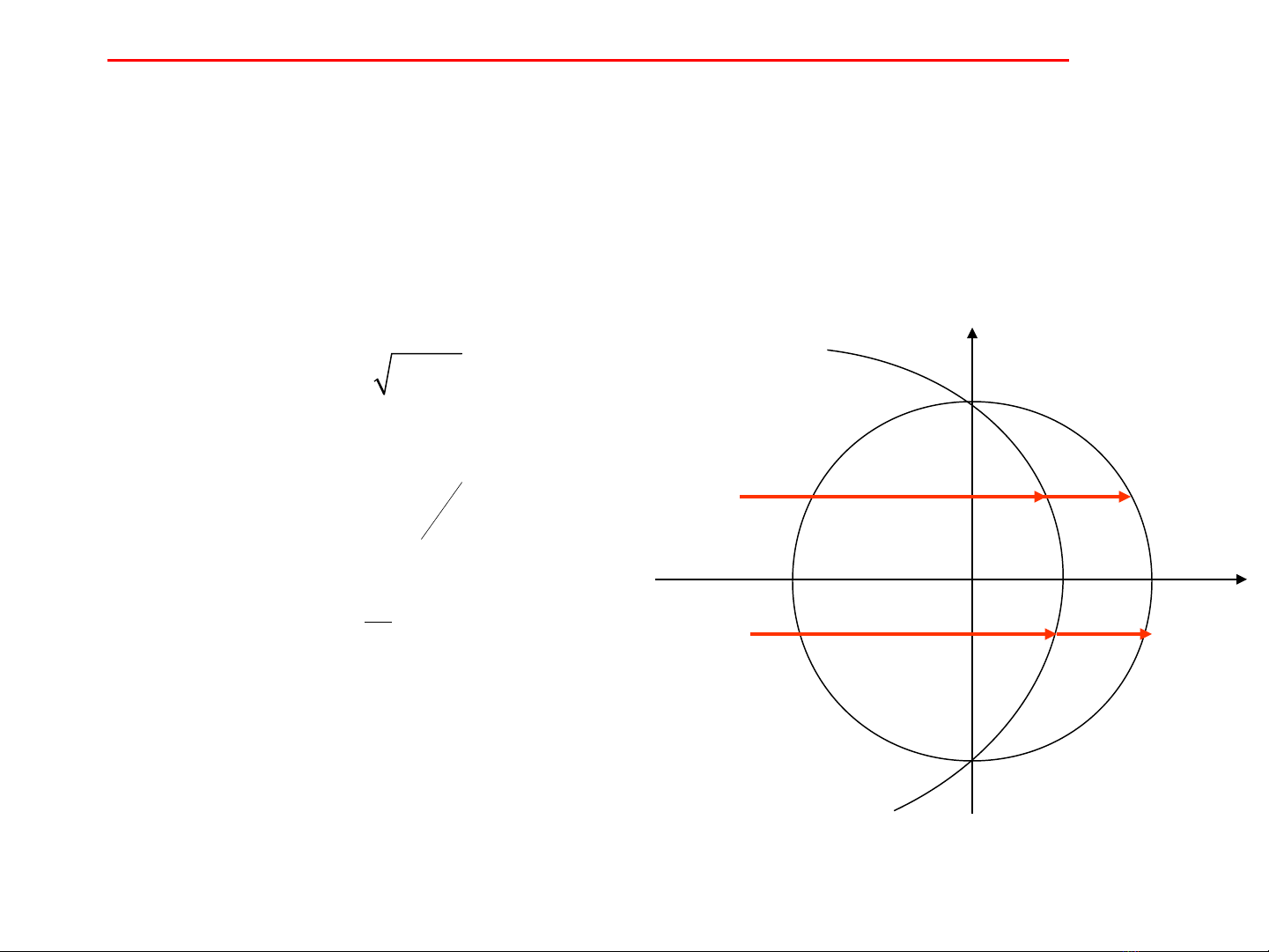
5. Tìm giao đi m c a 2 đ ng đã choể ủ ườ
4-4x=4-x2 ↔ x2-4x=0 ↔ x=0, x=4 (Lo i vì yạ2=4-4x<0)
Ta v hình đ có c n tích phân theo dxẽ ể ậ
2
-2
1
2
2
4
2
5
214
( )
y
y
S D dy dx
-
--
=� �
5
8
( ) 2 3
S D
p
= -