SV: Lê Hoàng Anh GVHD: Nguy n Tr ng Ph cễ ọ ướ
BÀI T P L N C H C K T C UẬ Ớ Ơ Ọ Ế Ấ
Mã Đ 3_2ề
S Đ AƠ Ồ
TÍNH D M GHÉP TĨNH Đ NHẦ Ị
I. N I DUNGỘ
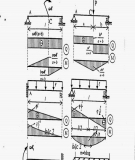
1. V l i s đ d m, kích th c, t i tr ng chính xác.ẽ ạ ơ ồ ầ ướ ả ọ
2. Xác đ nh các ph n l c và v bi u đ n i l c.ị ả ự ẽ ể ồ ộ ự
3. V đ ng nh h ng t i ti t di n k1 và k2.ẽ ườ ả ưở ạ ế ệ
4. Xác đ nh đ ng nh h ng t i k1 và k2 v a v .ị ườ ả ưở ạ ừ ẽ
II. BÀI LÀM
1.V l i s đ d m, kích th c, t i tr ng chính xác.ẽ ạ ơ ồ ầ ướ ả ọ
2.Xác đ nh các ph n l c và v bi u đ n i l cị ả ự ẽ ể ồ ộ ự
Xác đ nh ph n l c h ph và tính Mômen, l c c t.ị ả ự ệ ụ ự ắ
Vì trong h d m không có l c d c N nên ta không xét đ nệ ầ ự ọ ế .
Bài t p l n C H c K t C uậ ớ ơ ọ ế ấ 1

SV: Lê Hoàng Anh GVHD: Nguy n Tr ng Ph cễ ọ ướ
ΣMA = 0 => VB.3a = 3qa2 => VB = qa
ΣY = 0 => VB = VA = qa
Xét m t c t t i A:ặ ắ ạ
ΣM = 0 => M = 3qa2
ΣY = 0 => Q = - qa
Xét m t c t t i B:ặ ắ ạ
ΣM = 0 => M = 0
ΣY = 0 => Q = - qa
Xác đ nh ph n l c h ph và tính Mômen, l c c t.ị ả ự ệ ụ ự ắ
Bài t p l n C H c K t C uậ ớ ơ ọ ế ấ 2

SV: Lê Hoàng Anh GVHD: Nguy n Tr ng Ph cễ ọ ướ
ΣMD = 0 => VC.2a = 3qa2 + 2qa2 => VC = qa
ΣY = 0 => VC +VD = qa +2qa => VD = qa
Xét m t c t t i B:ặ ắ ạ
ΣM = 0 => M = 0
ΣY = 0 => Q = - qa
Xét m t c t t i bên trái C:ặ ắ ạ
ΣM = 0 => M = qa2
ΣY = 0 => Q = - qa
Xét m t c t t i bên ph i C:ặ ắ ạ ả
ΣM = 0 => M = qa2
ΣY = 0 => Q = qa - qa = 1,5qa
Xét m t c t t i D:ặ ắ ạ
ΣM = 0 => M = 0
ΣY = 0 => Q = - 0,5qa
Xác đ nh ph n l c h chính và tính Mômen, l c c t.ị ả ự ệ ự ắ
Bài t p l n C H c K t C uậ ớ ơ ọ ế ấ 3

SV: Lê Hoàng Anh GVHD: Nguy n Tr ng Ph cễ ọ ướ
ΣMF = 0 => MF = - ( 2qa2 + qa2 ) => MF = - 3 qa2
ΣY = 0 => VF = - ( 0,5qa +2qa ) => VF = 2,5qa
Xét m t c t t i D:ặ ắ ạ
ΣM = 0 => M = 0
ΣY = 0 => Q = - 0,5qa
Xét m t c t t i bên trái E:ặ ắ ạ
ΣM = 0 => M = - 0,5qa2
ΣY = 0 => Q = - 0,5qa
Xét m t c t t i bên ph i E:ặ ắ ạ ả
ΣM = 0 => M = - 0,5qa2
ΣY = 0 => Q = - 0,5qa - 2qa = - 2,5qa
Xét m t c t t i F:ặ ắ ạ
ΣM = 0 => M = - ( 2qa2 + qa2 ) = - 3qa2
ΣY = 0 => Q = - 0,5qa - 2qa = - 2,5qa
Bi u đ N I L Cể ồ Ộ Ự
Bài t p l n C H c K t C uậ ớ ơ ọ ế ấ 4

SV: Lê Hoàng Anh GVHD: Nguy n Tr ng Ph cễ ọ ướ
3. V đ ng nh h ng.ẽ ườ ả ưở
a. N u S h chính.ế ệ
P = 1 di đ ng h chính => H đ n gi n.ộ ệ ệ ơ ả
P = 1 di đ ng h ph .ộ ệ ụ
S = 0 t i v trí liên k t thanh theo ph ng đ ng.ạ ị ế ươ ứ
S b ng nhau t i kh p giao nhau.ằ ạ ớ
b. N u S h ph .ế ệ ụ
P = 1 di đ ng h chính => S = 0.ộ ệ
P = 1 di đ ng h ph => H đ n gi n.ộ ệ ụ ệ ơ ả
Bài t p l n C H c K t C uậ ớ ơ ọ ế ấ 5