
BÀI T P CH NG IẬ ƯƠ
Bài 1.1. Hãy nhân các ma tr n sau:ậ
a.
23
12
−
11
11
b.
−16
53
−23
12
c.
321
212
113
−
−
101
112
111
d.
103
112
01
12
13
ĐS: a.
−
−
15
13
b.
−
415
139
c.
−
−
418
116
126
d.
310
39
Bài 1.2.
1. Tính ma tr n ngh ch đ o c a các ma tr n sau:ậ ị ả ủ ậ
a)
=10
21
A
b)
−
=
100
210
321
B
2. Tìm h ng c a các ma tr n sau:ạ ủ ậ
a)
−
−
−−
=
28112
71524
42312
A
b)
−
−−
−
=
1977
7115
4312
1531
B
ĐS: 1.) a.
−
10
21
b.
−
−
100
210
721
2.) a.
2)( =A
ρ
b.
3)( =B
ρ
Bài 1.3. Tính các đ nh th c sau:ị ứ
a)
3111
1311
1131
1113
b)
201041
10631
4321
1111
c)
01
01
01
1110
cb
ca
ba
d)
yxyx
xyxy
yxyx
+
+
+
ĐS: a. 48 b. 1 c.
)(2
222 abacbccba ++−++
d.
)(2 33 yx +−
1
Bài 1.4. Tìm g c c a các hàm nh sauố ủ ả
a.
34
2
1713
2
2
)( ++
++
=
pp
pp
pA
b.
)2)(1(
79
2
5
3
)( ++
+++
=pp
ppp
pB
c.
617
2
17
3
7
4
2019
2
5
)( ++++
++
=
pppp
pp
pC
d.
ppp
pp
pD
25
2
6
3
7520
2
7
)( ++
−−
=
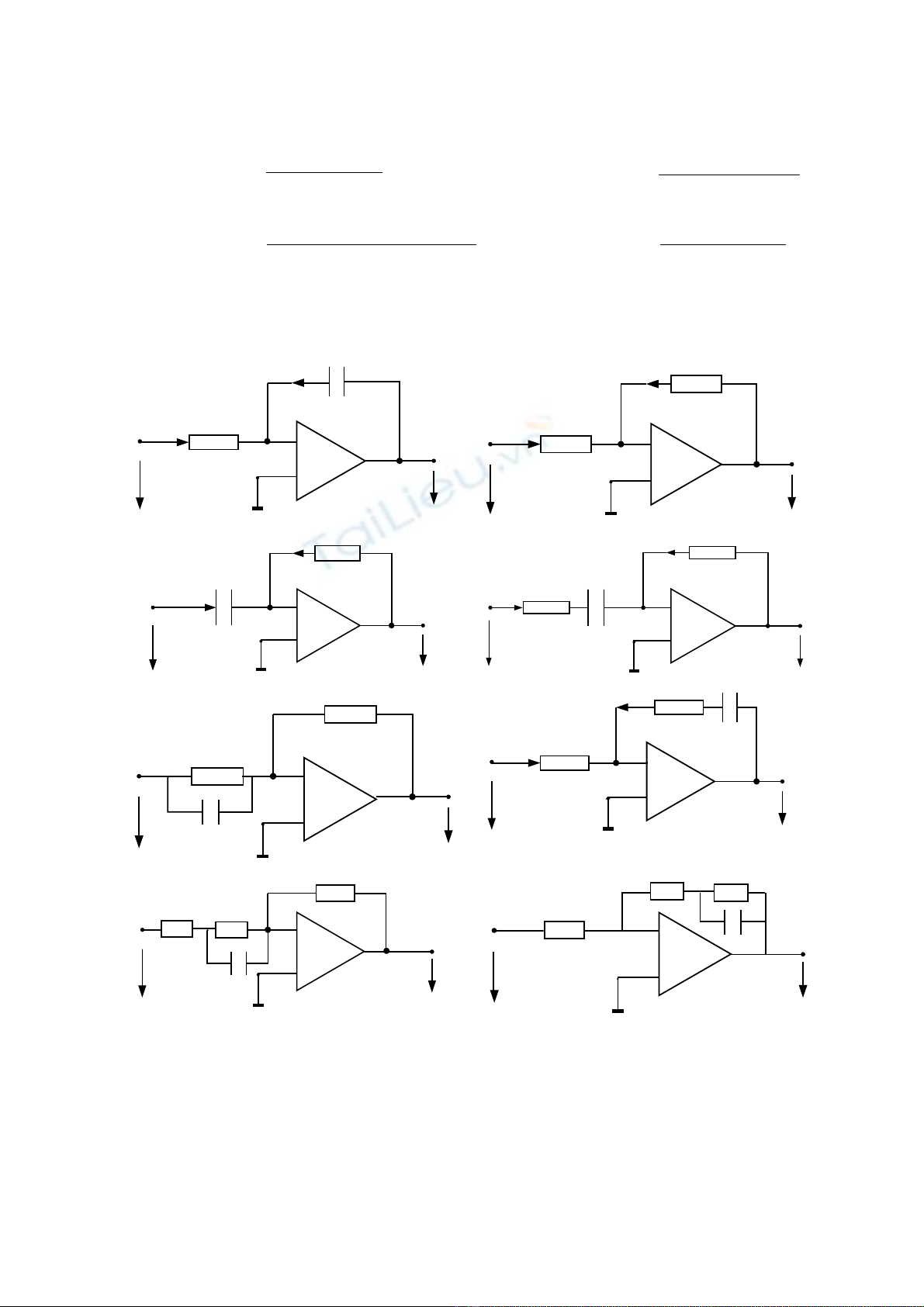
Bài 1.5. Hãy tìm hàm truy n c a các m ch đi u khi n s d ng khu ch đ i thu tề ủ ạ ề ể ử ụ ế ạ ậ
toán sau:
u
1
u
2
-
+
R
C
i
1
i
2
-
+
u
1
u
2
R
1
R
2
i
1
i
2
-
+
u1u2
C
R
i2
i1
-
+
u
1
u
2
C
R
R
1
-
+
u
1
u
2
R
1
R
2
i
1
i
2
C
u
1
u
2
-
+
RC
R
1
-
+
u
1
u
2
R
1
R
2
i
1
i
2
C
-
+
u
1
u
2
R
2
R
1
i
2
C
i
2
2
-
+
u
1
C
2
R
4
u
2
-
+
R
3
C
1
-
+
R
1
R
2
-
+
u
1
u
2
R
1
R
2
i
1
i
2
C
1
C
2
Hình 1.1
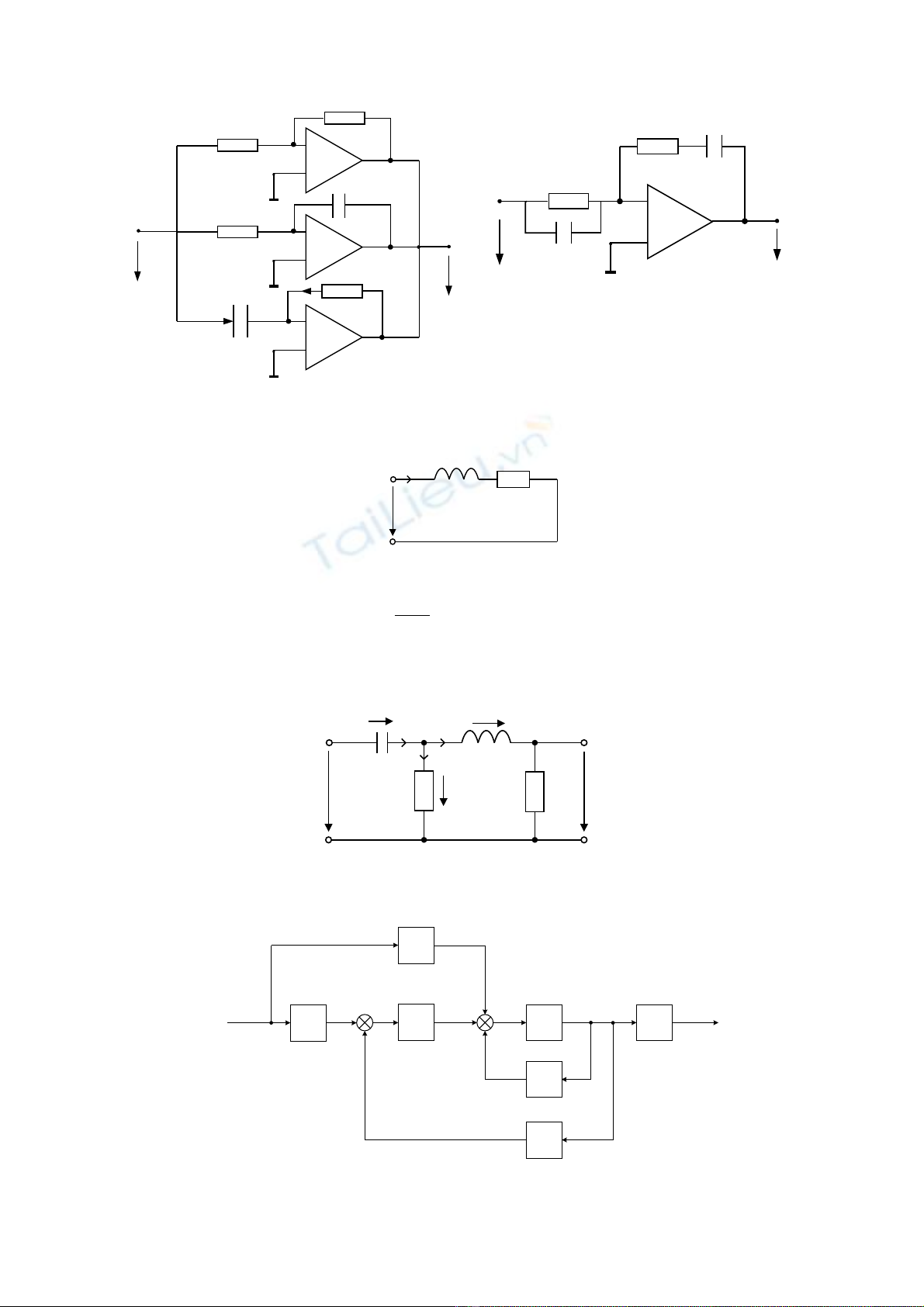
Bài 1.6. Cho s đ m ch đi n nh ơ ồ ạ ệ ư hình 1.2
u
R
L
i
Hình 1.2
Hãy tìm hàm truy n đ t ề ạ
U(s)
(s)
W(p) Ι
=
c a m ch bi t R = 1Ω, L = 2mH ?ủ ạ ế
Bài 1.7. Xác đ nh hàm truy n đ t c a m ch đi n nh ị ề ạ ủ ạ ệ ư hình 1.3
C
u
L
u
R
u
C
i
L
i
R
i
)(tu
)(ty
1
R
2
R
CL
Hình 1.3
Bài 1.8. Tìm hàm truy n đ t c a các h th ng có s đ kh i nh sau:ề ạ ủ ệ ố ơ ồ ố ư
1
G
4
G
3
G
6
G
)(−
7
G
)(−
)( pU
)( pΥ
5
G
2
G
3
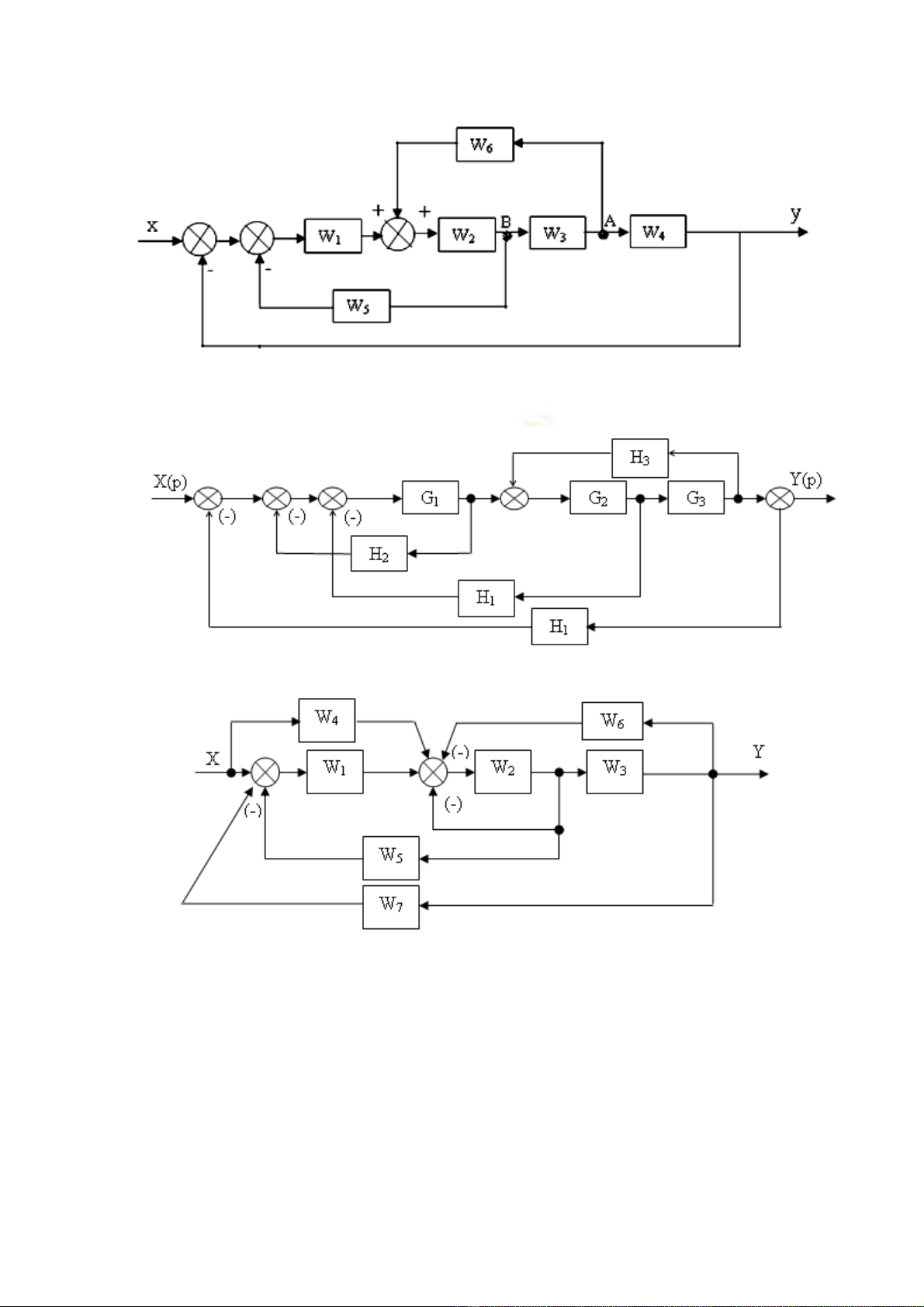
Hình 1.4
Bài 1.9. Tìm hàm truy n đ t t ng đ ng c a h th ng có s đ kh i nh hình :ề ạ ươ ươ ủ ệ ố ơ ồ ố ư
Hình 1.5a
Hình 1.5b
4
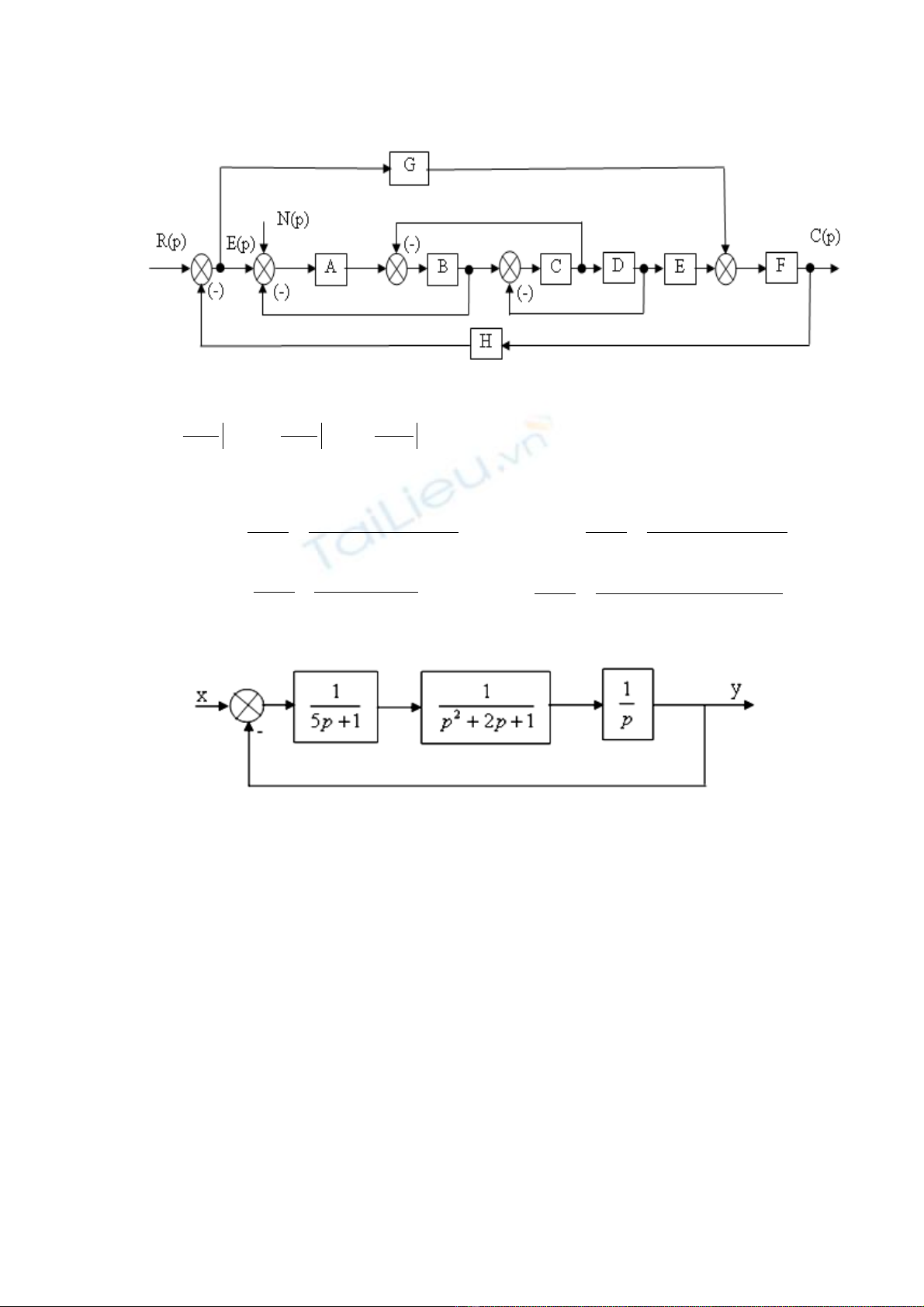
Bài 1.9.
Hình 1.6
Tính:
0)(
)(
)(
=sN
sR
sC
,
0)(
)(
)(
=sN
sE
sC
,
0)(
)(
)(
=sR
sN
sC
cho h th ng trên?ệ ố
Bài 1.10. Chuy n các hàm truy n sau sang ph ng trình tr ng thái:ể ề ươ ạ
a.
2.2.32
6.2.3
)(
)(
)( 23
2
1+++
++
== ppp
pp
pU
pY
pW
b.
5.2.3
4.2.6
)(
)(
)( 23
23
2+++
+++
== ppp
ppp
pU
pY
pW
c.
2.2.3
6.2
)(
)(
)( 2
3++
+
== pp
p
pU
pY
pW
d.
2.5.32
1.2
)(
)(
)( 234
23
4++++
+++
== pppp
ppp
pU
pY
pW
Bài 1.11. Tìm hàm truy n c a h th ng có s đ c u trúc sau, t đó suy ra PTTTề ủ ệ ố ơ ồ ấ ừ
Hình 1.7
5


























