
§2 Các đ nh lý c b n v c p bài toán đ i ị ơ ả ề ặ ố
ng uẫ
1. M i quan h gi a c p bài toán đ i ng uố ệ ữ ặ ố ẫ
2. ng d ng c a bài toán đ i ng u: Ứ ụ ủ ố ẫ
2. 1. Tìm PAT c a bài toán đ i ng uƯ ủ ố ẫ
2. 2. Ch ng t tính t i u c a m t ph ng ứ ỏ ố ư ủ ộ ươ
án 2. 3. Gi i bài toán có d ng đ c bi t.ả ạ ặ ệ
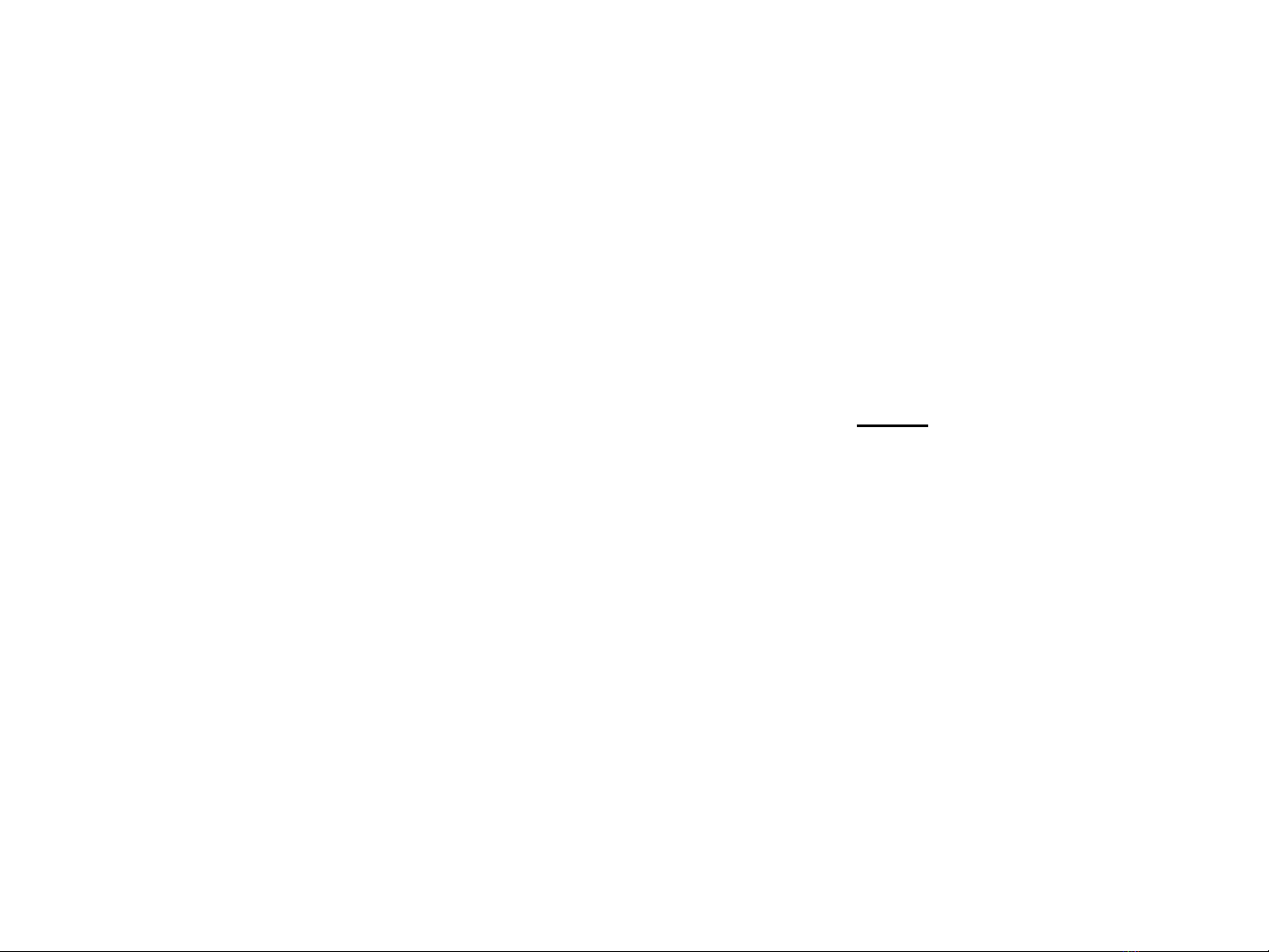
M i quan h gi a c p bài toán đ i ng uố ệ ữ ặ ố ẫ
1 1 2 2 m m
11 1 21 2 m1 m 1 1
1n 1 2n 2 mn m n n
g(y) b y b y ...... b y Max (Min)
a y a y ...... a y c ( c )
....................................................
a y a y ...... a y c ( c )
= + + +
+ + +
+ + +
1 1 2 2 n n
11 1 12 2 1n n 1
m1 1 m2 2 mn n m
j
f (x) c x c x ...... c x Min (Max)
a x a x ...... a x b
....................................................
a x a x ...... a x b
x 0 j 1, n
= + + +
+ + + =
+ + + =
∀ =
Bài toán đ i ng u:ố ẫ

M i quan h gi a c p bài toán đ i ng uố ệ ữ ặ ố ẫ
M i quan h gi a hai bài toán đ c th hi n ố ệ ữ ượ ể ệ
trong các đ nh lý sau: ị
Đ nh lý 1:ị Đ i v i c p bài toán đ i ng u bao gi ố ớ ặ ố ẫ ờ
cũng ch x y ra m t trong 3 tr ng h p sau:ỉ ẩ ộ ườ ợ
- C hai bài toán đ u không có ph ng án. ả ề ươ
- C hai bài toán đ u có ph ng án, lúc đó ả ề ươ
c hai bài toán đ u có PAT và giá tr hàm m c ả ề Ư ị ụ
tiêu c a chúng b ng nhau ủ ằ
- M t trong 2 bài toán không có ph ng án, ộ ươ
bài toán kia có ph ng án, khi y bài toán có ươ ấ
ph ng án s không có PAT .ươ ẽ Ư

M i quan h gi a c p bài toán đ i ng uố ệ ữ ặ ố ẫ
H qu 1:ệ ả N u m t trong 2 bài toán đ i ng u có ế ộ ố ẫ
PAT thì bài toán kia cũng có PATƯ Ư

M i quan h gi a c p bài toán đ i ng uố ệ ữ ặ ố ẫ
H qu 2:ệ ả x0, y0 là hai ph ng án c a bài toán (I), ươ ủ
(I’), khi đó x0, y0 là PAT khi và ch khi Ư ỉ
f(x0) = g(y0)
Ch ng minh:ứ
Đi u ki n c n:ề ệ ầ Đ c suy t đ nh lý trênượ ừ ị
Đi u ki n đ : ề ệ ủ
G i x’ là ph ng án b t kì c a bài toán (I), ọ ươ ấ ủ
khi đó ta có:
n n m m n
, 0 , , 0
j j ij i j ij j i
j 1 j 1 i 1 i 1 j 1
m
0 0 0
i i
i 1
f (x ') c x a y x a x y
b y g(y ) g(x )
= = = = =
=
� � � �
= =
� � � �
� � � �
= = =
� �� ��


























