Chöông 1. Ngoân ngöõ Logic
Tröông Myõ Dung 4
1. NGOÂN NGÖÕ LOGIC.
1.1. Meänh ñeà - Baûng chaân trò.
1.1.1. Ñònh nghóa.
Moät Meänh ñeà laø moät caâu phaùt bieåu (ñoái töôïng Toaùn hoïc) maø ta coù theå noùi ngay
raèng caâu ñoù ñuùng hoaëc sai.
Thí duï. “8 laø moät soá chaún” laø moät Meänh ñeà ñuùng.
“3 < 2 “ laø moät Meänh ñeà sai.
“x laø moät soá nguyeân, x<10” khoâng phaûi laø Meänh ñeà.
“Anh coù khoûe khoâng” khoâng phaûi laø Meänh ñeà.
Hai meänh ñeà p vaø q ñöôïc goïi laø töông ñoàng neáu chuùng cuøng ÑUÙNG hoaëc cuøng
SAI, kyù hieäu p = q.
1.1.2. Baûng chaân trò.
Ñeå bieåu dieãn giaù trò ÑUÙNG hoaëc SAI cuûa moät meänh ñeà p ngöôøi ta duøng Baûng
chaân trò.
p
T
F
Hoaëc
p
0
1
Caùc kyù hieäu:
T,1 chæ giaù trò ÑUÙNG,
F, 0 chæ giaù trò SAI.
Neáu caàn phaûi xeùt hai meänh ñeà p vaø q cuøng luùc thì ta coù baûng chaân trò vôùi 4
tröôøng hôïp.
p q
0 0
0 1
1 0
1 1
Chöông 1. Ngoân ngöõ Logic
Tröông Myõ Dung 5
Toång quaùt neáu coù n meänh ñeà caàn xeùt cuøng luùc thì baûng chaân trò goàm 2n
tröôøng hôïp.
1.2. Phuû ñònh cuûa moät Meänh ñeà.
Phuû ñònh cuûa Meänh ñeà p laø moät meänh ñeà, kyù hieäu p coù giaù trò SAI neáu
p ÑUÙNG vaø coù giaù trò ÑUÙNG neáu p SAI.
Thí duï. Neáu p : “2 + 2 = 4” thì phuû ñònh cuûa p laø meänh ñeà
p :” 2 + 2 ≠ 4”.
p p
1 0
1 0
1.3. Caùc pheùp noái logic.
Caùc meänh ñeà coù theå ñöôïc keát hôïp laïi ñeå ñöôïc moät Meänh ñeà hôïp baèng caùch söû
duïng caùc pheùp noái logic. Caùc pheùp noái logic goàm coù:
q Pheùp noái lieàn (tuyeån) (“vaø”).
q Pheùp hôïp (“hay”).
q Pheùp keùo theo.
q Pheùp töông ñöông.
q Pheùp hôïp coù loaïi tröø.
1.3.1. Pheùp Noái lieàn (tuyeån).
Tuyeån hai meänh ñeà p vaø q kyù hieäu p ∧ q (ñoïc laø “p vaø q”) hoaëc p.q chæ
coù giaù trò ÑUÙNG khi caû hai cuøng ÑUÙNG.
Baûng chaân trò cuûa p ∧ q nhö sau :
p q p ∧ q
1
1
0
0
1
0
1
0
1
0
0
0
Thí duï: p :”3 < 5”; q : “4 ≠ 2 + 2”. Ta coù :
p ∧ q :”3 < 5” vaø “4 ≠ 2 + 2” laø Meänh ñeà sai.
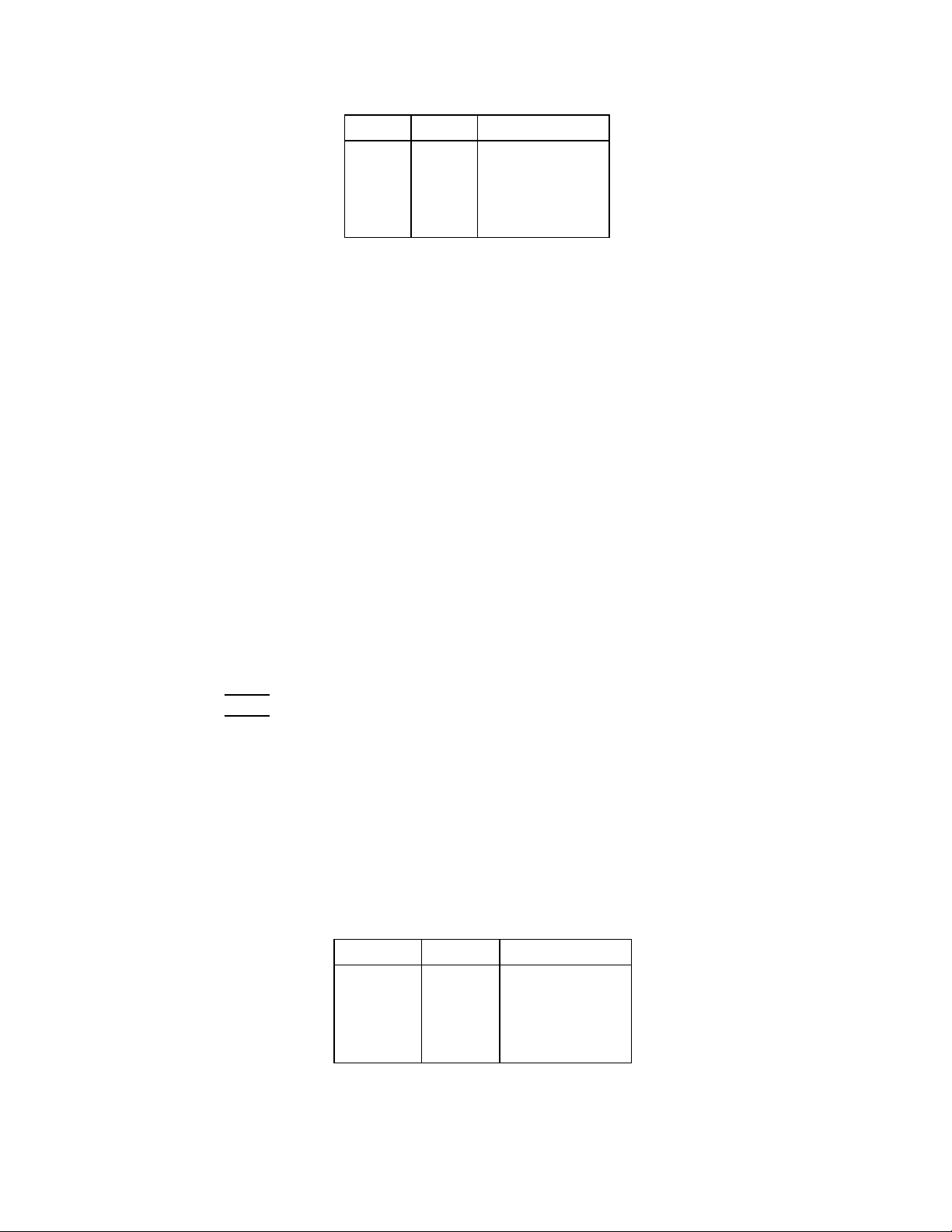
1.3.2. Pheùp hôïp.
Hôïp cuûa hai meänh ñeà p vaø q laø meänh ñeà p∨q (ñoïc laø “p hay q”) hoaëc p+q,
coù giaù trò ÑUÙNG neáu ít nhaát moät trong hai meänh ñeà treân ÑUÙNG vaø coù giaù trò
SAI neáu caû hai cuøng SAI.
Chöông 1. Ngoân ngöõ Logic
Tröông Myõ Dung 6
Baûng chaân trò cuûa p ∨ q nhö sau :
P p
q p ∨ q
1
1
0
0
1
0
1
0
1
1
1
0
Thí duï: p :”3 < 5”; q : “4 ≠ 2 + 2”. Ta coù :
p∨q :”3 < 5” vaø q : “4 ≠ 2 + 2” laø Meänh ñeà ÑUÙNG.
1.3.3. Caùc tính chaát cuûa pheùp tuyeån, pheùp hôïp.
a. Luõy ñaúng p ∧ p = p p ∨ p = p
Ñoái xöùng p ∧ q = q ∧ p p ∨ q = q ∨ p
Keát hôïp p ∧ (q∧ r) = (p∧q)∧ r p ∨(q ∨ r)= (p∨ q) ∨r
p ∧ p = ∅ p ∨ p = I
p ∧ I = p p ∨ I = I
p ∧ ∅ = ∅ p ∨ ∅ = p
∅ kyù hieäu meänh ñeà luoân luoân coù giaù trò SAI goïi laø NGHÒCH ÑEÀ.
I kyù hieäu meänh ñeà luoân luoân coù giaù trò ÑUÙNG goïi laø CHAÂN ÑEÀ.
b. Tính phaân phoái.
p ∧ (q ∨ r) = (p ∧ q) ∨ (p ∧ q).
p ∨ (q ∧ r) = (p ∨ q) ∧ (p ∨ q).
c. Qui luaät DE MORGAN.
(p∧q) = p ∨ q
(p∨q) = p ∧ q
Chuù yù. Taäp hôïp caùc meänh ñeà vôùi caùc pheùp noái ∧, ∨ vaø pheùp phuû ñònh thoûa caùc tính
chaát neâu treân goïi laø moät heä ñaïi soá BOOLE.
1.3.4. Pheùp keùo theo logic.
Pheùp keùo theo logic cuûa meänh ñeà p vaø meänh ñeà q kyù hieäu p ⇒ q (ñoïc laø
“neáu p thì q”) chæ SAI khi p ÑUÙNG vaø q SAI.
Baûng chaân trò cuûa p ⇒ q nhö sau :
p q p⇒q
1
1
0
0
1
0
1
0
1
0
1
1
Chöông 1. Ngoân ngöõ Logic
Tröông Myõ Dung 7
Thí duï:
”3 < 5” ⇒ “3 < 7” laø Meänh ñeà ÑUÙNG.
“4:soá nguyeân toá”⇒ø “TP.HCM laø thuû ñoâ cuûa VN” laø Meänh ñeà ÑUÙNG.
“5:soá nguyeân toá” vaø “TP.HCM laø thuû ñoâ cuûa VN” laø Meänh ñeà SAI.
Chuù yù.
a. Pheùp keùo theo logic khoâng coù yù nghóa gì veà nguyeân nhaân vaø haäu quaû ñoái vôùi
p vaø q.
b. Neáu (p ⇒ q) ÑUÙNG vaø p ÑUÙNG thì q phaûi ÑUÙNG.
Neáu (p ⇒ q) ÑUÙNG vaø q SAI thì p phaûi SAI.
c. Neáu p ÑUÙNG, muoán chöùng minh (p ⇒ q) ÑUÙNG thì ta phaûi chöùng minh
q ÑUÙNG.
CAÙC TÍNH CHAÁT CUÛA PHEÙP KEÙO THEO LOGIC.
(p⇒ p) = I
(p ⇒q) = (q ⇒ p)
[(p⇒q) vaø (q⇒r)] ⇒ (p⇒r) laø moät chaân ñeà.
(p⇒q) = (p ∨ q).
1.3.5. Pheùp töông ñöông Logic.
Pheùp töông ñöông cuûa hai meänh ñeà p vaø q laø meänh ñeà kyù hieäu p⇔q (ñoïc laø
“p töông ñöông q” hoaëc “p neáu vaø chæ neáu q” xaùc ñònh bôûi (p⇒q) vaø
(q⇒p).
Baûng chaân trò cuûa p ⇔ q nhö sau :
p q p⇒q q ⇒ p p⇔q
1
1
0
0
1
0
1
0
1
0
1
1
1
1
0
1
1
0
0
1
Nhö vaäy:
+ Neáu p = q thì (p ⇔q) ÑUÙNG vaø ngöôïc laïi.
+ Neáu (p ⇔ q) ÑUÙNG thì p = q.
Tính chaát:
+ p ⇔ p laø moät chaân ñeà.
+ p ⇔ q = q ⇔ p
+ (p⇔q) vaø (q⇔r) ⇒ (p⇔r) laø moät chaân ñeà.
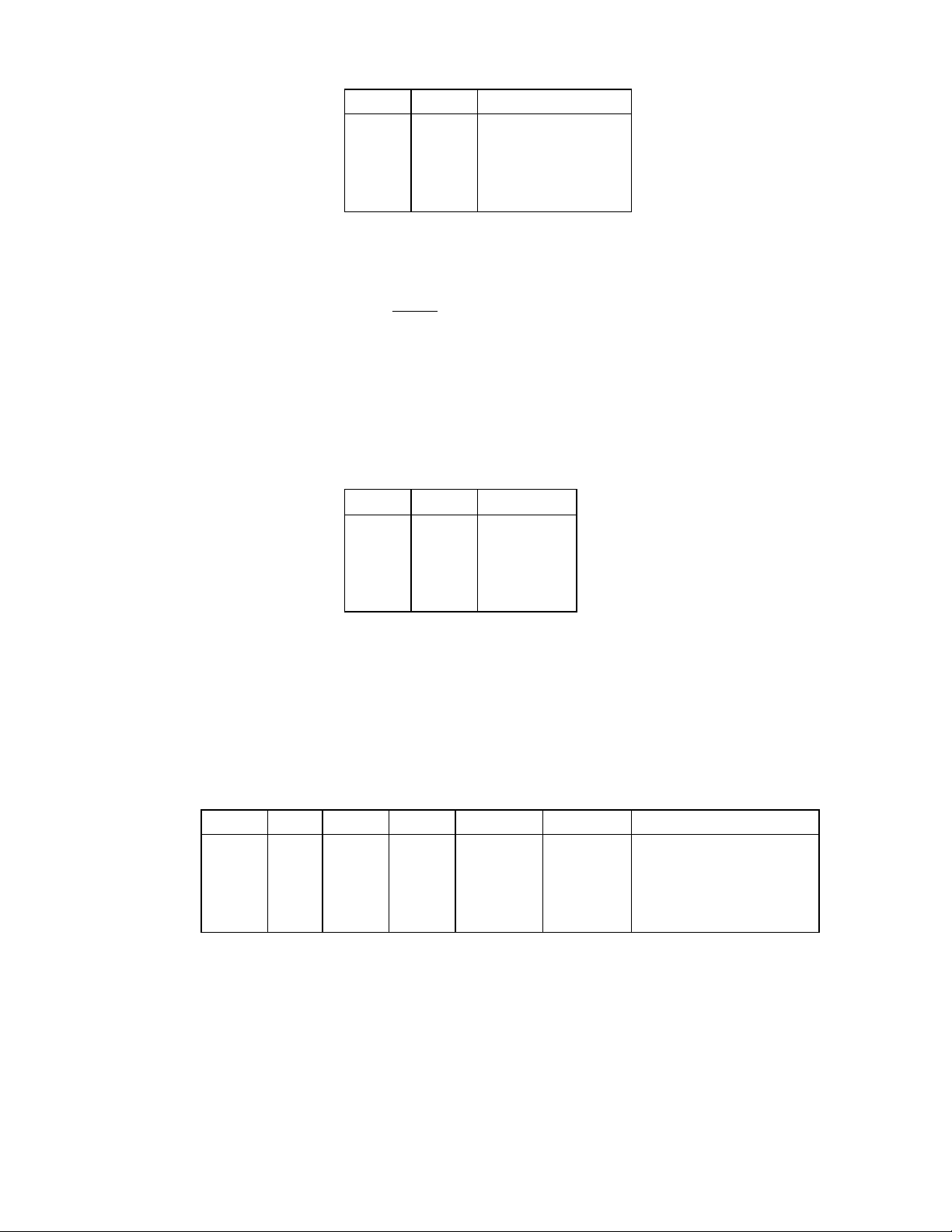
1.3.6. Pheùp hôïp coù loaïi tröø.
Ta goïi pheùp hôïp coù loaïi tröø cuûa hai meänh ñeà p vaø q laø meänh ñeà p⊕q (ñoïc laø
“p chæ hoaëc q”) coù giaù trò ÑUÙNG neáu chæ moät trong hai meänh ñeà ñoù ÑUÙNG
vaø coù giaù trò sai neáu caû hai cuøng SAI hoaëc cuøng ÑUÙNG.
Chöông 1. Ngoân ngöõ Logic
Tröông Myõ Dung 8
Baûng chaân trò cuûa p ⊕ q nhö sau :
p P p
q p ⊕ q
1
1
0
0
1
0
1
0
0
1
1
0
Tính chaát:
p⊕p = I
p⊕q = q⊕p
p⊕q = p⊕q = (p⊕q) = (p⇔q).
p⊕(q⊕r) = (p⊕q)⊕r = p⊕q⊕r.
1.4. Xaùc ñònh moät meänh ñeà hôïp coù baûng chaân trò cho tröôùc.
Giaû söû ta coù hai meänh ñeà p, q cho saún. Ta muoán tìm moät meänh ñeà R do p,
q (vaø caû p, q) hôïp thaønh baèng caùc töø noái ∨, ∧ sao cho giaù trò ÑUÙNG,
SAI cuûa R ñöôïc cho bôûi baûng:
p P p
q R
1
1
0
0
1
0
1
0
0
1
1
0
Phöông Phaùp.
1. Chuù yù tröôøng hôïp R coù giaù trò ÑUÙNG (haøng 2 vaø 3).
2. Trong moãi tröôøng hôïp ôû böôùc 1, ta tìm Meänh ñeà (M.Ñ) Tuyeån ÑUÙNG trong moãi
tröôøng hôïp ñoù vaø SAI trong caùc tröôøng hôïp khaùc.
Haøng 2 cho M.Ñ tuyeån p ∧ q. Haøng 3 cho M.Ñ tuyeån p ∧ q.
3. Hôïp caùc meänh ñeà tuyeån ôû Böôùc 2, ta ñöôïc meänh ñeà R phaûi tìm laø:
R = (p ∧q) ∨ (p ∧ q)
Ñeå kieåm tra laïi, ta laäp baûng chaân trò:
p
q p q p ∧q p∧ q (p∧q)∨ (p∧q)
1
1
0
0
1
0
1
0
0
0
1
1
0
1
0
1
0
1
0
0
0
0
1
0
0
1
1
0
Thí duï. Moät ngöôøi tuø bò giam ñöôïc cho moät cô hoäi ñeå thoaùt. Phoøng giam coù hai cöûa: Moät
cöûa thoaùt vaø moät cöûa daãn ñeán chuoàng coïp. Moãi cöûa coù moät ngöôøi canh, nhöng ngöôøi naøy chæ
traû lôøi caâu hoûi baèng ÑUÙNG hay SAI. Moät trong hai ngöôøi ñoù thì luoân luoân noùi thaät, vaø ngöôøi
kia thì luoân luoân noùi doái. Ngöôøi tuø khoâng bieát ai laø ngöôøi noùi thaät, cöûa naøo laø cöûa thoaùt vaø
anh chæ ñöôc pheùp ñaët moät caâu hoûi. Vaäy anh phaûi ñaët caâu hoûi nhö theá naøo ñeå thoaùt ra ñöôïc?