CHUYÊN ð DÃY S (BDHSG)
1. KHÁI NIM DÃY S
1) Cho A là mt tp con khác rng ca tp s nguyên ,ℤ hàm s u : A →ℝ
n
n u(n) u=֏
ñưc gi là mt dãy s, và kí hiu là n
(u ) hoc
{
}
n
u. Thông thưng ta hay chn A sao cho phn t nh nht
ca A là 1. Dãy (u
n
) gi là dãy s hu hn (hoc dãy s vô hn) nu A là tp hp gm hu hn (vô hn) phn t.
S u
n
ñưc gi là s hng tng quát ca dãy (u
n
).
2) Dãy s (u
n
) ñưc gi là dãy s tăng (tăng không nghim ngt, gim, gim không nghiêm ngt) nu n n 1
u u +
<
(tương ng n n 1
u u +
≤, n n 1
u u +
>, n n 1
u u +
≥) vi mi n A.∈
3) Dãy s (u
n
) ñưc gi là tun hoàn nu tn ti s nguyên dương k sao cho n k n
u u , n A.
+= ∀ ∈ S k nh nht
tho mãn tính cht này ñưc gi là chu kì ca dãy tun hoàn (u
n
). Nu k = 1 thì ta ñưc mt dãy hng (tt c các
s hng bng nhau).
4) Dãy s (u
n
) ñưc gi là b chn trên nu tn ti s thc M sao cho n
u M≤ vi mi n A.∈ Dãy s (u
n
) ñưc
gi là b chn dưi nu tn ti s thc m sao cho n
u m≥ vi mi n A.∈ Dãy s (u
n
) ñưc gi là b chn (hoc
gii ni) nu nó va b chn trên va b chn dưi, tc là tn ti s thc M, m sao cho n
m u M≤ ≤ vi mi
n A,∈ hoc tn ti s thc C sao cho n
u C, n A.≤ ∀ ∈ Dãy s hu hn hoc tun hoàn thì luôn b chn.
2. CP S
1) Cp s cng
- Dãy s (u
n
) ñưc gi là cp s cng nu mi s hng ñu tho mãn n 1 n
u u d
+− = (d: hng s, gi là công sai).
- Công thc truy hi: n 1 n
u u d.
+= + Công thc s hng tng quát: n 1
u u (n 1)d, n A.= + − ∀ ∈ Công thc tính
tng n s hng ñu tiên: n 1 n 1 1
n n n(n 1)
S (u u ) (2u (n 1)d) nu d.
2 2 2
−
= + = + − = + Tính cht các s hng:
k 1 k 1 k
u u 2u .
+ −
+ =
2) Cp s nhân
- Dãy s (u
n
) ñưc gi là cp s nhân nu mi s hng ñu tho mãn n 1 n
u u .q
+= (q: hng s, gi là công bi).
- Công thc truy hi: n 1 n
u u .q.
+= Công thc s hng tng quát: n 1
n 1
u u .q .
−
= Công thc tính tng n s hng
ñu tiên: n 1
S nu= nu q = 1, n 1
n 1 1 q
S u 1 q
+
−
=− nu q 1.≠ Tính cht các s hng: 2
k 1 k 1 k
u .u u .
+ − =
3) Cp s nhân cng
- Dãy s (u
n
) ñưc gi là cp s nhân cng nu mi s hng ñu tho mãn n 1 n
u u .q d
+= + (q, d là hng s).
4) Cp s ñiu hoà
- Dãy s (u
n
) ñưc gi là cp s ñiu hoà nu mi s hng ca nó ñu khác 0 và tho mãn n 1 n 1
nn 1 n 1
2u u
u ,
u u
− +
− +
=+
hay
n n 1 n 1
1 1 1 1
( ).
u 2 u u
− +
= + (Hc sinh t ôn tp các dng toán v cp s)
3. XÁC ðNH S HNG TNG QUÁT CA DÃY S
3.1. D ðOÁN S HNG TNG QUÁT VÀ CHNG MINH BNG QUI NP
BÀI TP
1) Xác ñnh s hng tng quát ca dãy s cho b i:
n
1 n 1 1 n 1 n
n
2n
1 n 1 n n 1 n 1
n
u
a)u 1,u , n 1,2,3,... b)u 2, u 2 u , n 1,2,3,...
1 u
3 1 ( 3 1)u3 5 3 1
c)u 1,u u u 1, n 1,2,3,... d)u ,u , n 1,2,3,.
2 2 3 1 3 1 ( 3 1)u
+ +
+ +
= = ∀ = = = + ∀ =
+
− + +−
= = − + + ∀ = = = ∀ =
+ + − −
..
xa.nguyenvan@gmail.com
www.VNMATH.com
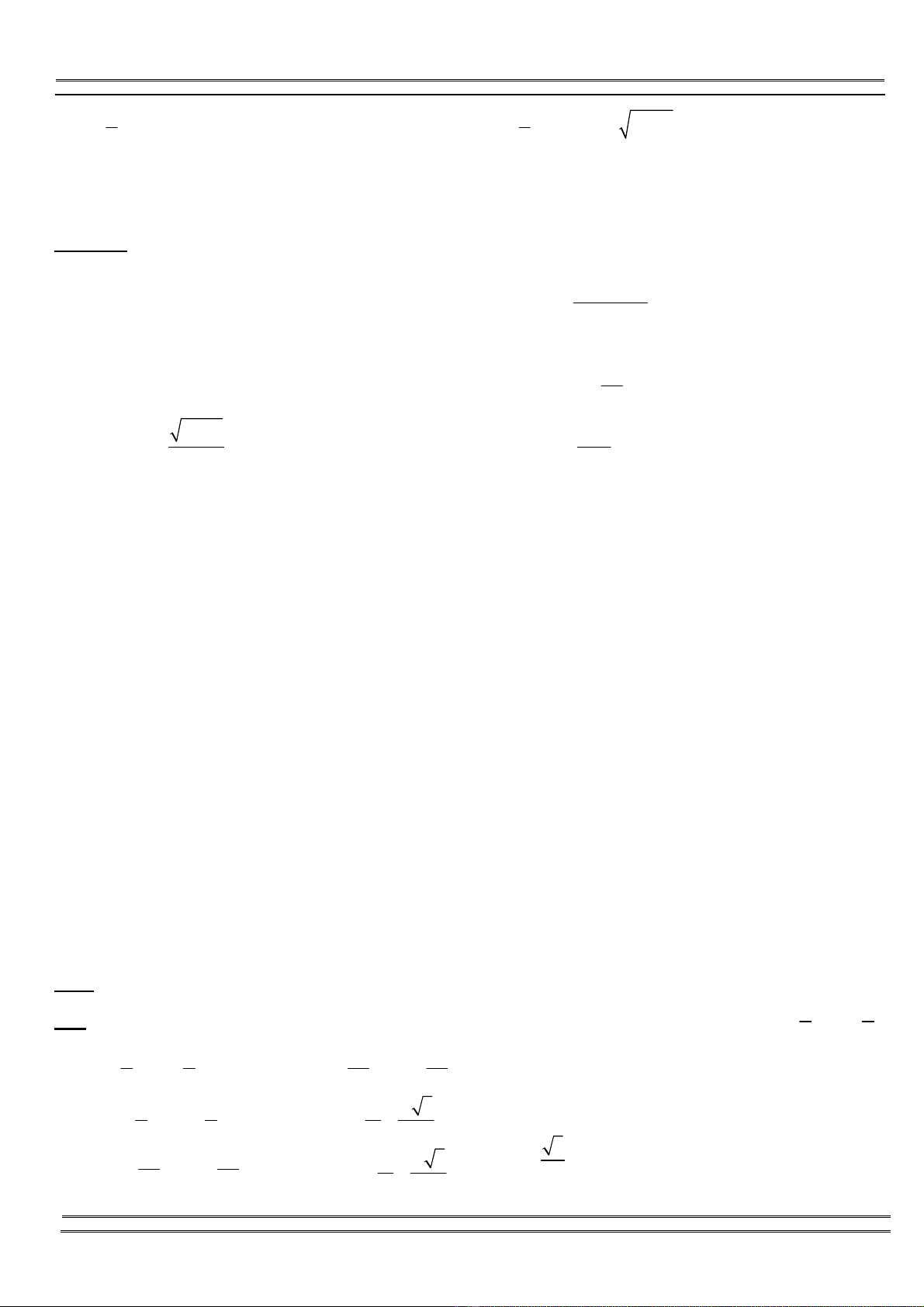
2 2
1 n 1 n 1 n 1 n n
1 1
e)u ,u 2u 1, n 1,2,3,... f )u ,u 2u 1 u , n 1,2,3,...
2 2
+ +
= = − ∀ = = = − ∀ =
3.2. MT S DNG TRUY HI ðC BIT
Vi dãy s cho b i công thc truy hi dng n 1 n
u u f (n)
+= + thì n 1
u u f (1) f (2) ... f (n 1).= + + + + −
Vi dãy s cho b i công thc truy hi dng n 1 n
u u .g(n)
+= thì n 1
u u .g(1).g(2)...g(n 1).= −
BÀI TP
2) Xác ñnh s hng tng quát ca dãy s cho b i:
2n
1 n 1 n 1 n 1
3 2 n
1 n 1 n 1 n 1 n
1 n 1 n
(n 1) u
a)u 1, u u n!.n, n 1, 2,3,... b)u 1, u , n 1,2,3,...
n(n 2)
c)u 1,u u n 3n 3n 1, n 1,2,3,... d)u 3, u u 3 , n 1, 2,3,...
e)u 1,u u (n 1).
+ +
+ +
+
+
= = + ∀ = = = ∀ =
+
= = + + − + ∀ = = = + ∀ =
= = + + n1 n 1 n
2
1 n 1 n 1 n 1 n
1
2 , n 1,2,3,... f)u 2,u 2 , n 1,2,3,...
u
n 1 n
g)u 1, u u , n 1,2,3,... h)u 0,u (1 u ), n 1,2,3,...
n n 1
+
+ +
∀ = = = − ∀ =
−
= = ∀ = = = + ∀ =
+
3.3. PHƯƠNG TRÌNH ðC TRƯNG
Ta ch! xét hai trưng hp ñơn gin sau ñây:
a) Xét dãy s (u
n
) cho b i 1 2 n 2 n 1 n
u ,u ,u a.u b.u , n * (a,b const).
+ +
= + ∀ ∈ =ℕ Khi ñó phương trình 2
x ax b 0− − =
ñưc gi là phương trình ñc trưng ca dãy s ñã cho.
Nu phương trình trên có hai nghim thc phân bit 1 2
x ,x thì n n
n 1 2
u A.x B.x .= +
Nu phương trình trên có hai nghim thc trùng nhau 1 2
x x= thì n
n 1
u (A nB).x .= +
Nu phương trình trên có 0∆ < , gi hai nghim phc ca nó là 1 2
x ,x , và bi"u di#n hai s phc này dng
lưng giác 1 2
x r(cos i.sin ), x r(cos i.sin ),= ϕ+ ϕ = ϕ− ϕ vi r, ϕ là các s thc, r là môñun ca 1
x và 2
x ,
[
)
0;2 ,
ϕ∈ π
i là ñơn v o, thì n
n
u r (A.cos n B.sinn ).= ϕ+ ϕ ($ ñó các hng s A, B ñưc xác ñnh nh 1 2
u ,u )
b) Xét dãy s (u
n
) cho b i 1 2 3 n 3 n 2 n 1 n
u ,u ,u ,u a.u b.u c.u , n * (a,b,c const)
+ + +
= + + ∀ ∈ =ℕ có phương trình ñc
trưng 3 2
x ax bx c 0.− − − =
Nu phương trình trên có ba nghim thc phân bit 1 2 3
x ,x , x thì n n n
n 1 2 3
u A.x B.x C.x .= + +
Nu phương trình trên có ba nghim thc 1 2 3
x ,x ,x mà 1 2 3
x x x≠ = thì n n
n 1 2
u A.x (B nC).x .= + +
Nu phương trình trên có ba nghim thc 1 2 3
x ,x , x và 1 2 3
x x x= = thì 2 n
n 1
u (A nB n C).x .= + +
Nu phương trình trên có ba nghim 1 2 3
x ,x , x trong ñó 1
x là nghim thc, còn hai nghim
2
x r(cos i.sin ),= ϕ+ ϕ 3
x r(cos i.sin )= ϕ− ϕ là hai nghim phc (không phi là s thc) thì
n n
n 1
u A.x r (B.cos n C.sinn ).= + ϕ+ ϕ ($ ñó các hng s A, B, C ñưc xác ñnh nh 1 2 3
u ,u ,u )
VD1. Cho dãy s n
(u ) xác ñnh b i 1 2 n 2 n 1 n
u 1,u 0,u u u , n *.
+ +
= = = − ∀ ∈ℕ Chng minh n
(u ) b chn.
HD. Phương trình ñc trưng ca dãy s ñã cho là 2
x x 1 0− + = có hai nghim phc
1
x cos i.sin ,
3 3
π π
= +
2
x cos i.sin ,
3 3
π π
= − nên
n
n
n n
u 1 (A.cos B.sin ), n *.
3 3
π π
= + ∀ ∈ℕ Do
1 2
u 1,u 0,= = nên ta có
1
2
A B 3 A 1
1 A.cos B.sin ( u ) 1
3 3 2 2 .
3
2 2 B
A B 3
0 A.cos B.sin ( u ) 03
3 3 2 2
π π
=
= + = + =
⇔ ⇔
π π =
= + = − + =
TÂM SÁNG – CHÍ BN
xa.nguyenvan@gmail.com
www.VNMATH.com

Suy ra nn 3 n
u cos .sin , n *.
3 3 3
π π
= + ∀ ∈ℕ Vy
2 2
n
n 3 n 3 2
u cos .sin 1 ( ) , n *,
3 3 3 3 3
π π
= + ≤ + = ∀ ∈ℕ hay
n
(u ) là dãy b chn.
VD2. Cho n
(u ) có 1 2 3 n 3 n 2 n 1 n
u 0,u 16,u 47,u 7u 11u 5u , n *.
+ + +
= = = = − + ∀ ∈ℕ Tìm dư khi chia 2011
u cho 2011.
HD. Phương trình ñc trưng 3 2
x 7x 11x 5 0− + − = có 3 nghim thc 1
x 5= (nghim ñơn), 2 3
x x 1= = (nghim
kép) do ñó n n
n
u A.5 (B nC).1 , n *.= + + ∀ ∈ℕ Vì 1 2 3
u 0,u 16,u 47= = = nên 1
A ,B 13,C 12.
5
= = − = Suy ra
n 1
n
u 5 12n 13, n *.
−
= + − ∀ ∈ℕ T ñó 2010
2011
u 5 12.2011 13.= + − Theo ñnh lí Phécma thì 2010
5 1 2011−⋮ (ñnh
lí Phécma: Nu p là s nguyên t, a là s nguyên và (a, p) = 1, thì p 1
a 1 (mod p)).
−≡ Vy 2011
u chia cho 2011 dư
12− (hay dư 1999).
VD3. Cho hai dãy s n n
(x ),(y ) tho mãn 1 1 n 1 n n n 1 n n
x y 1, x 4x 2y , y x y , n *.
+ +
= = = − = + ∀ ∈ℕ Xác ñnh công
thc ca n n
x , y .
HD. Ta có n 2 n 1 n 1 n 1 n n n 1 n n n 1 n n 1 n
x 4x 2y 4x 2(x y ) 4x 2x 2y 4x 2x x 4x
+ + + + + + +
= − = − + = − − = − + − hay
n 2 n 1 n
x 5x 6x ( n *).
+ +
= − ∀ ∈ℕ Dãy n
(u ) có phương trình ñc trưng 2
x 5x 6 0 x 2− + = ⇔ = hoc x = 3. Suy ra
n n
n
x A.2 B.3 , n *.= + ∀ ∈ℕ Mà 1 2 1 1
x 1,x 4x 2y 2,= = − = nên 1
A ,B 0,
2
= = và ta có n 1
n
x 2 , n *.
−
= ∀ ∈ℕ T
ñó và n 1
n 1 n n n
x 4x 2y y 2 .
−
+= − ⇒= Vy n 1
n n
x y 2 , n *.
−
= = ∀ ∈ℕ
3.4. PHƯƠNG PHÁP DÃY S PH
VD4. Cho dãy s n 1 2 n 2 n 1 n
(u ) : u 1,u 2,u 2.u u 1, n *.
+ +
= = = − + ∀ ∈ℕ ðt n n 1 n
v u u .
+
= − Chng minh n
(v ) là
cp s cng và tìm n
u .
HD. a) Ta có 1 2 1
v u u 1.= − = Và n 2 n 1 n n 2 n 1 n 1 n
u 2.u u 1, n * u u u u 1, n *
+ + + + +
= − + ∀ ∈ ⇔ − = − + ∀ ∈ℕ ℕ
n 1 n
v v 1, n *.
+
⇔ = + ∀ ∈ℕ Vy n
(v ) là cp s cng vi s hng ñu tiên 1
v 1,= công sai d = 1.
b) T câu a ta có n 1
v v (n 1).d 1 (n 1).1 n,= + − = + − = hay n 1 n
u u n, n *.
+− = ∀ ∈ℕ Suy ra n n n 1 n 1 n 2
u (u u ) (u u )
− − −
= − + − +
2
2 1 1 (n 1).n n n
... (u u ) u [(n 1) (n 2) ... 2 1] 1 1 1, n *.
2 2 2
−
+ + − + = − + − + + + + = + = − + ∀ ∈ℕ
VD5. Cho dãy s
n 1 2 n 2 n 1 n
2 1
(u ) : u 0,u 1, u .u u , n *.
3 3
+ +
= = = + ∀ ∈ℕ ðt
n n 1 n
v u u .
+
= − Chng minh
n
(v ) là
cp s nhân và tìm
n
u .
HD. Ta có
1 2 1
v u u 1.= − = Và
n 2 n 1 n n 2 n 1 n
2 1
u .u u , n * 3u 2u u , n *
3 3
+ + + +
= + ∀ ∈ ⇔ = + ∀ ∈ ⇔ℕ ℕ
n 2 n 1 n 1 n
3(u u ) (u u ), n *
+ + +
− = − − ∀ ∈ℕn 1 n
1
v v , n *.
3
+−
⇔ = ∀ ∈ℕ Vy
n
(v ) là cp s nhân vi s hng ñu tiên
1
v 1,= công bi 1
q .
3
= −
Ta có n 1 n 1
n 1 1
v v .q ( ) ,
3
− −
= = − n *.∀ ∈ℕ Suy ra n n n 1 n 1 n 2 2 1 1 n 1 n 2
u (u u ) (u u ) ... (u u ) u v v
− − − − −
= − + − ++ + − + = + +
n 1
2 n 2
2 1 1 n
1
1 ( )
1 1 1 3 9
3
... v v u 0 1 ( ) ( ) ... ( ) 1. , n *.
1
3 3 3 4 4.( 3)
1 ( )
3
−
−
− −
+ + + + = + + − + − + + − = = + ∀ ∈
−
− −
ℕ
VD6. Tìm s hng tng quát ca dãy s ( n
u) có
1 1
, . , *,
+
= = + + ∀ ∈ℕ
n
n
u c u q u an d n ñó a, c, d, q là hng s.
xa.nguyenvan@gmail.com
TÂM SÁNG – CHÍ BN
www.VNMATH.com
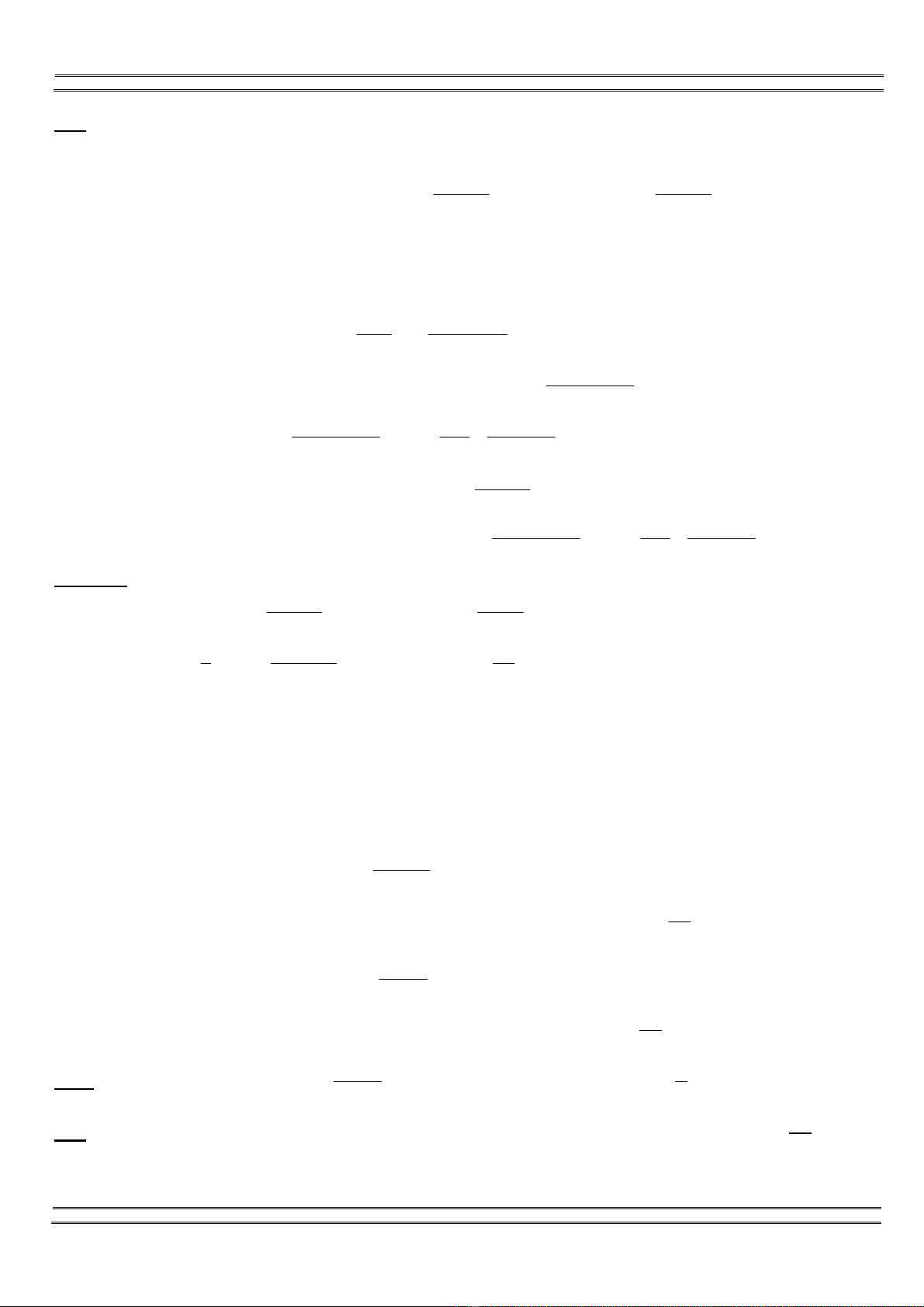
HD. Vi q = 1 thì 1, *
n
n
u u an d n
+= + + ∀ ∈ℕ. Ta nhn thy 2 1 3 2
u u a d,u u 2a d,...,= + + = + +
n 1 n 2 n n 1 2 3 n 1 n 1 2 n 2 n 1
n 1 n
... ...
n(n 1) n(n 1)
a(1 2 ... (n 2) (n 1)) (n 1)d a (n 1)d c a (n 1)d, (n *).
2 2
u u (n 2)a d,u u (n 1)a d u u u u u u u u
u u u
− − − − − −
⇒+ + + + = + + + + +
− −
+ + + + − + − + − = + + − ⇒= + + − ∈
= + − + = + − +
⇒ℕ
Khi q ≠ 1, ta s& xét mt dãy ph' ( n
v) tha mãn , *,
n n
u v bn e n= + + ∈ℕ ñó b, e là nhng hng s, và ta c
g(ng chn b, e thích hp ñ" ( n
v) là cp s nhân. T ñ)ng thc truy hi ban ñu ta có
1
( ) ( ), *,
+
= + + − + + − − ∈ℕ
n n
v qv qb a b n qe d b e n và d# thy ñ" ( n
v) là cp s nhân thì cn có
qb a b+ − =qe d b e+ − − = 0 2,(q 1),
1( 1)
a d a qd
b e
qq≠
− −
⇔ = =
−−. Lúc này (vi b, e như trên) do 1n n
v qv
+=
nên ( n
v) là cp s nhân có công bi q. Suy ra n
v=
1
1
.n
qv−=1
12
( ).
( 1)
n
aq dq d
u q
q
−
+ −
+−, t ñó ta tính ñưc s hng
tng quát ca ( n
u) là 1
122
.
( ). 1( 1)
( 1)
n
naq dq d d a qd
a n
u u q qq
q
−
=+ − − −
+ + +
−−
− (n ≥2).
Vy, s hng tng quát ca ( n
u) ñã cho là : 1
22
( 1) ( 1) , 1
2
, 1
.
( ). 1( 1)
( 1)
−
−
+ + − =
=
≠
+ − − −
+ + +
−−
−
nn
n n
c a n d khi q
khi q
uaq dq d d a qd
a n
c q qq
q
.
BÀI TP
3) Cho n
(u ) : n
1 n 1 n
3 2u
u 0,u , n *.
4 u
++
= = ∀ ∈
+ℕ ðt n
nn
u 1
v .
u 3
−
=+ Chng minh n
(v ) là cp s nhân và tìm n
u .
4) Cho n
(u ) :
n
1 n 1
(n 1)u
1
u ,u , n *.
3 3n
+
+
= = ∀ ∈ℕ ðt
n
n
u
v .
n
= Chng minh
n
(v ) là cp s nhân và tìm
n
u .
5) Cho
n
(u ) : n
1 n 1 n
u 1, u u 2.(1 3 ), n *. +
= = + + ∀ ∈ℕ ðt n
n n
v u 3 .= − Chng minh dãy s n
(v ) là cp s
cng và tìm n
u .
6) Nêu cách xác ñnh s hng tng quát ca dãy s ( n
u) cho b i 1,u c=1( ) . , *
n
nP nu q u n
+= + ∀ ∈ℕ, ñó c, q
là các hng s, còn P(n) là mt ña thc bc k cho trưc.
3.5. TUYN TÍNH HOÁ MT S DÃY PHI TUYN
a) Vi dãy s n
(x ) cho b i n
1 n 1 n
px q
x a, x , n *,
rx s
++
= = ∀ ∈
+ℕ và a, p, q, r, s là các hng s, ta xét hai dãy n
(u ),
n
(v ) tho mãn 1 1 n 1 n n n 1 n n
u a, v 1, u pu qv , v ru sv , n *,
+ +
= = = + = + ∀ ∈ℕ thì n
nn
u
x .
v
= T ñó tìm ra n n n
u , v , x .
b) Vi dãy s n
(x ) cho b i 2
n
1 n 1 n
x d
x a, x , n *,
2x
++
= = ∀ ∈ℕ và a, d là các hng s, d 0,≠ta xét hai dãy n
(u ),
n
(v ) tho mãn 2 2
1 1 n 1 n n n 1 n n
u a, v 1, u u dv ,v 2u v , n *,
+ +
= = = + = ∀ ∈ℕ thì n
nn
u
x .
v
= T ñó tìm ra n n n
u , v , x .
VD7. Cho dãy n
(x ) có n
1 n 1 n
x
x 1, x , n *,
2 x
+
= = ∀ ∈
+ℕ tìm n
x và chng minh n1
x , n 2.
n
< ∀ ≥
HD. Xét hai dãy n
(u ), n
(v ) tho mãn 1 1 n 1 n n 1 n n
u v 1,u u , v u 2v , n *,
+ +
= = = = + ∀ ∈ℕ thì n
nn
u
x .
v
= Ta thy
n
x 1, n *.= ∀ ∈ℕ Và n 1 n n 1 n
v 2v 1, n * v 1 2(v 1), n *.
+ +
= + ∀ ∈ ⇔ + = + ∀ ∈ℕ ℕ Suy ra 2
n n 1 n 2
v 1 2.(v 1) 2 (v 1)
− −
+ = + = + =
TÂM SÁNG – CHÍ BN
xa.nguyenvan@gmail.com
www.VNMATH.com

n 1 n n
1 n
... 2 (v 1) 2 v 2 1, n *.
−
= = + = ⇒= − ∀ ∈ℕ Vy n
nn
n
u1
x , n *.
v2 1
= = ∀ ∈
−ℕ Ta có n 0 1 n
n n n
2 C C ...C= + + >
0 1
n n
C C 1 n, n 2,> + = + ∀ ≥ tc là nn
1 1
x , n 2.
n
2 1
= < ∀ ≥
−
VD8. Cho dãy n
(x ) có n
0 n 1 n
2x 1
x 2, x , n ,
2 x
++
= = ∀ ∈
+ℕ tìm n
x và tìm phn nguyên ca 1 2 n
S x x ... x .= + + +
HD. Xét hai dãy n
(u ), n
(v ) tho mãn 0 0 n 1 n n n 1 n n
u 2,v 1,u 2u v , v u 2v , n ,
+ +
= = = + = + ∀ ∈ℕ thì n
nn
u
x .
v
= Ta
có 1 0 0 n 2 n 1 n 1 n 1 n n n 1 n n 1 n n 2 n 1 n
u 2u v 5,u 2u v 2u u 2v 2u u 2(u 2u ) u 4u 3u ,
+ + + + + + + +
= + = = + = + + = + + − ⇒= −
phương trình 2
x 4x 3 0 x 1, x 3,− + = ⇔ = = nên n
n
u A B.3 , n .= + ∀ ∈ℕ Do 0 1
u 2,u 5= = nên 1 3
A , B .
2 2
= =
Suy ra n 1
n3 1
u , n .
2
++
= ∀ ∈ℕ Tính ñưc n 1
n3 1
v , n .
2
+−
= ∀ ∈ℕ Vy n 1
nn 1
3 1
x , n .
3 1
+
+
+
= ∀ ∈
−ℕ ðt
2 3 n n 1
1 2 n 2 3 n n 1
3 1 3 1 3 1 3 1
S x x ... x ... .
3 1 3 1 3 1 3 1
+
−
+ + + +
= + + + = + + + +
− − − − Lưu ý
n 1
nn 1 n 1
3 1 2
x 1 1, n .
3 1 3 1
+
+ +
+
= = + > ∀ ∈
− − ℕ Ta có
n 1 0 1 2 2 n 1 n 1 0 2 2
n 1 n 1 n 1 n 1 n 1 n 1 1
(1 2) C C .2 C .2 ... C .2 C C .2 1 (n 1)n. .4 2n(n 1) 1, n *.
2
+ + +
+ + + + + +
+ = + + + + ≥ + = + + = + + ∀ ∈ℕ
D*n ti n 1 nn 1
2 1 1 1
3 1 2n(n 1), n * x 1 1 1 , n *.
n(n 1) n n 1
3 1
++
− ≥ + ∀ ∈ ⇒= + ≤ + = + − ∀ ∈
+ +
−
ℕ ℕ Do vy vi
n *∀ ∈ℕ thì 1 2 n 1 1 1 1 1 1 1
S x x ... x (1 ) (1 ) ... (1 ) n 1 n 1.
1 2 2 3 n n 1 n 1
= + + + ≤ + − + + − + + + − = + − < +
+ + Mt khác
1 2 n
S x x ... x n, n *.= + + + > ∀ ∈ℕ Như vy n S n 1, *,< < + ∀∈ℕ nên
[
]
S n, *.= ∀∈ℕ
4. MT S BÀI TOÁN LIÊN QUAN TI TÍNH CHT CA DÃY S
VD9. Cho các s dương 1 2 13
a ,a ,...,a tho mãn 1 2 13
a a ... a 13.+ + + ≥ Chng minh dãy (u
n
) cho b i
n n n
n 1 2 13
u a a ... a , n *,= + + + ∀ ∈ℕ là dãy tăng không nghiêm ngt.
HD. Vi mi s dương a và s nguyên dương n ta có n
(a 1)(a 1) 0− − ≥ nên n 1 n
a a a 1.
+− ≥ − T ñó suy ra
n 1 n 1 n 1 n n n
n 1 n 1 2 13 1 2 13 1 2 13
u u (a a ... a ) (a a ... a ) a a ... a 13 0, n *,
+ + +
+− = + + + − + + + ≥ + + + − ≥ ∀ ∈ℕ hay n 1 n
u u , n *.
+≥ ∀ ∈ℕ
Vy (u
n
) là dãy s tăng không nghiêm ngt.
VD10. Chng minh dãy s (u
n
) cho b i u
1
= 1, nn 1
1
u , n 2,3,4...
3 u −
−
= ∀ =
+ là dãy s gim và b chn.
HD. * Trưc ht ta chng minh n3 5
u , n *.
2
− +
> ∀ ∈ℕ Tht vy, vi n = 1 thì 13 5
u 1 .
2
− +
= > Gi s
k3 5
u .
2
− +
> Khi ñó k k 1
k k
3 5 1 2 3 5 1 3 5
3 u u .
2 3 u 2 3 u 2
3 5 +
+ − − − +
+ > ⇒< = ⇒= >
+ +
+ Theo nguyên lí
qui np toán hc, ta có n3 5
u , n *,
2
− +
> ∀ ∈ℕ tc là (u
n
) b chn dưi b i 3 5 .
2
− +
* Bây gi ta xét hiu 2
n n
n n 1 n n
n n
u 3u 1
1 3 5
u u u 0, n *, do u , n *.
3 u 3 u 2
++ + − +
− = + = > ∀ ∈ > ∀ ∈
+ + ℕ ℕ Vy (u
n
)
là dãy s gim.
* Vì (u
n
) gim nên 1 2 n n 1
1 u u ... u u ...
+
= > > > > > suy ra (u
n
) b chn trên b i 1. Vy (u
n
) là dãy s b chn.
TÂM SÁNG – CHÍ BN
xa.nguyenvan@gmail.com
www.VNMATH.com


























