Đáp án Điều khiển tự động (AUCO330329), Đề 01, HỌC KỲ I, 2016-2017
CÂU 1:
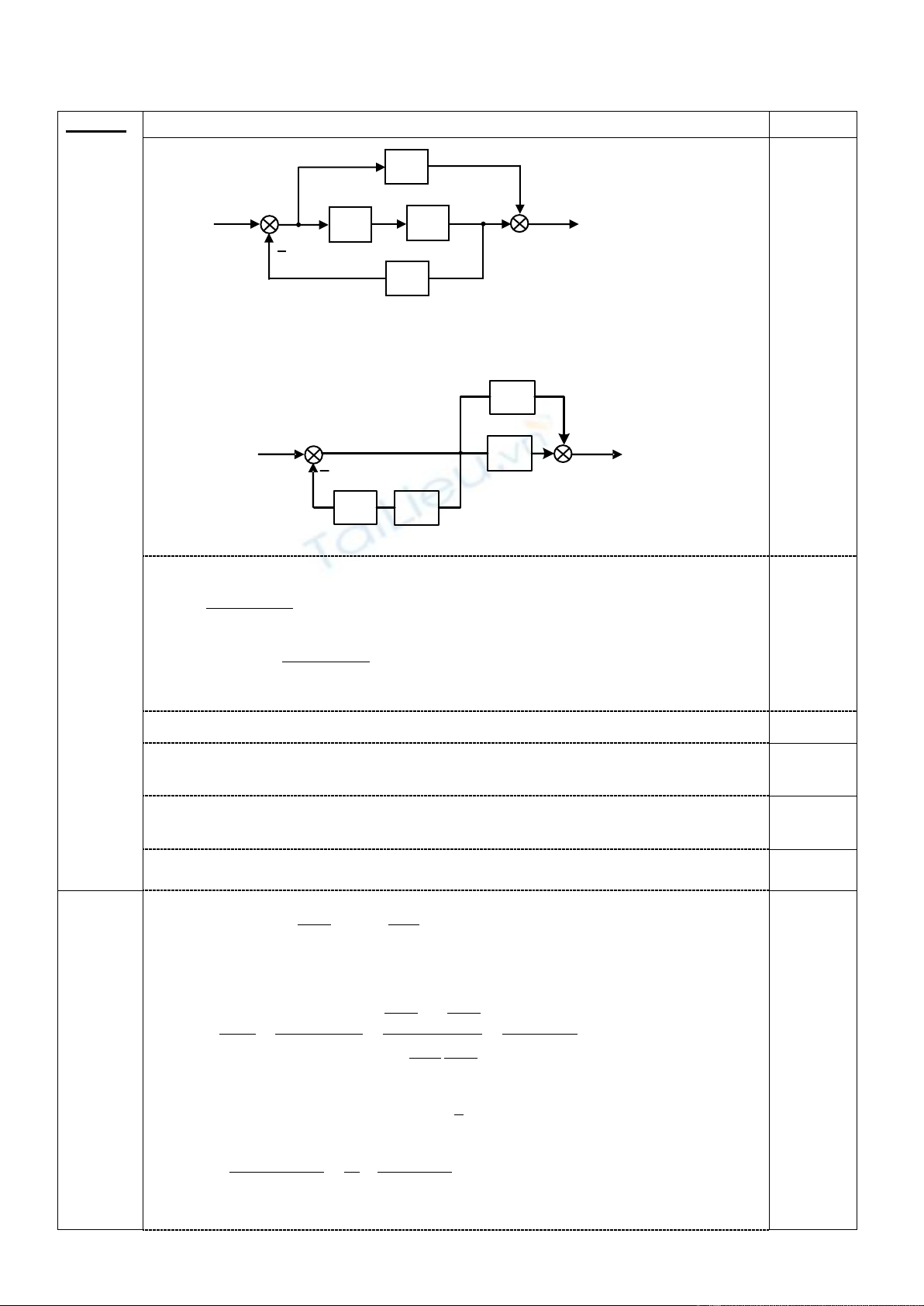
a.(1đ)
Đáp án Cách 1.
Điểm
Chuyển điểm nhánh sau G2 ra trước G1
R(s) Y(s)
H2
12
GG
12
GG
H1
0.5
td1 1 1 2
G H G G
1 1 2
td td1 td2 2 1 2
H G G
G G G 1 H G G

0.5
Đáp án Cách 2: SV có thể sử dụng Graph tín hiệu
Điểm
Vẽ lại sơ đồ theo dạng Graph tín hiệu:
0.25
Tìm số đường tiến, vòng kín
0.5
Hàm truyền của hệ thống tính theo công thức Mason:
0.25
b. (1đ)
1
G2
;
211
GHs3

;
21
Hs1
Hàm truyền tương đương:
1 1 2
td 2
2 1 2
11
2
H G G
Y(s) 3(s 1)
s 3 s 3
G (s) 12
R(s) 1 H G G s 4s 5
1s 1 s 3



Tín hiệu vào là hàm step, suy ra:
1
R(s) s
22
3(s 1) A Bs C
Y(s) s(s 4s 5) s s 4s 5

0.5
R(s)
Y(s)
G2
H1
H2
G1
Trang 2
A B 0
4A C 3
5A 3

A 3/5
B 3/5
C 3/5
2 2 2
3/ 5 3/ 5s 3/5 3/ 5 3 s 2 3
Y(s) s (s 2) 1 s 5 (s 2) 1 (s 2) 1



2t 2t
33
y(t) e cost 3e sin t
55

2t
3 3 10 1 3
y(t) e cost sin t
55 10 10



2t
3 3 10
y(t) e cos(t )
55
; với
1
cos 10

0.5
0.5
0.5
CÂU 2
(4 điểm)
Đáp án
Điểm
a (0.5đ) Hàm truyền hệ hở:
0.1s
hc 2
5000(s 20)e
G (s) G (s)G(s)H(s) (s 4)(s 50) s 12s 100

0.5
b (2đ). Vẽ biểu đồ Bode biên độ của hệ hở:
Đưa hàm truyền về dạng tổng quát:
0.1s
h2
2
1
5000.20( s 1)e
20
G (s) 1 1 1
4.50.100( s 1)( s 1) s 0.12s 1
4 50 10



Nhận xét: Khâu trễ không ảnh hưởng đến biểu đồ Bode biên độ
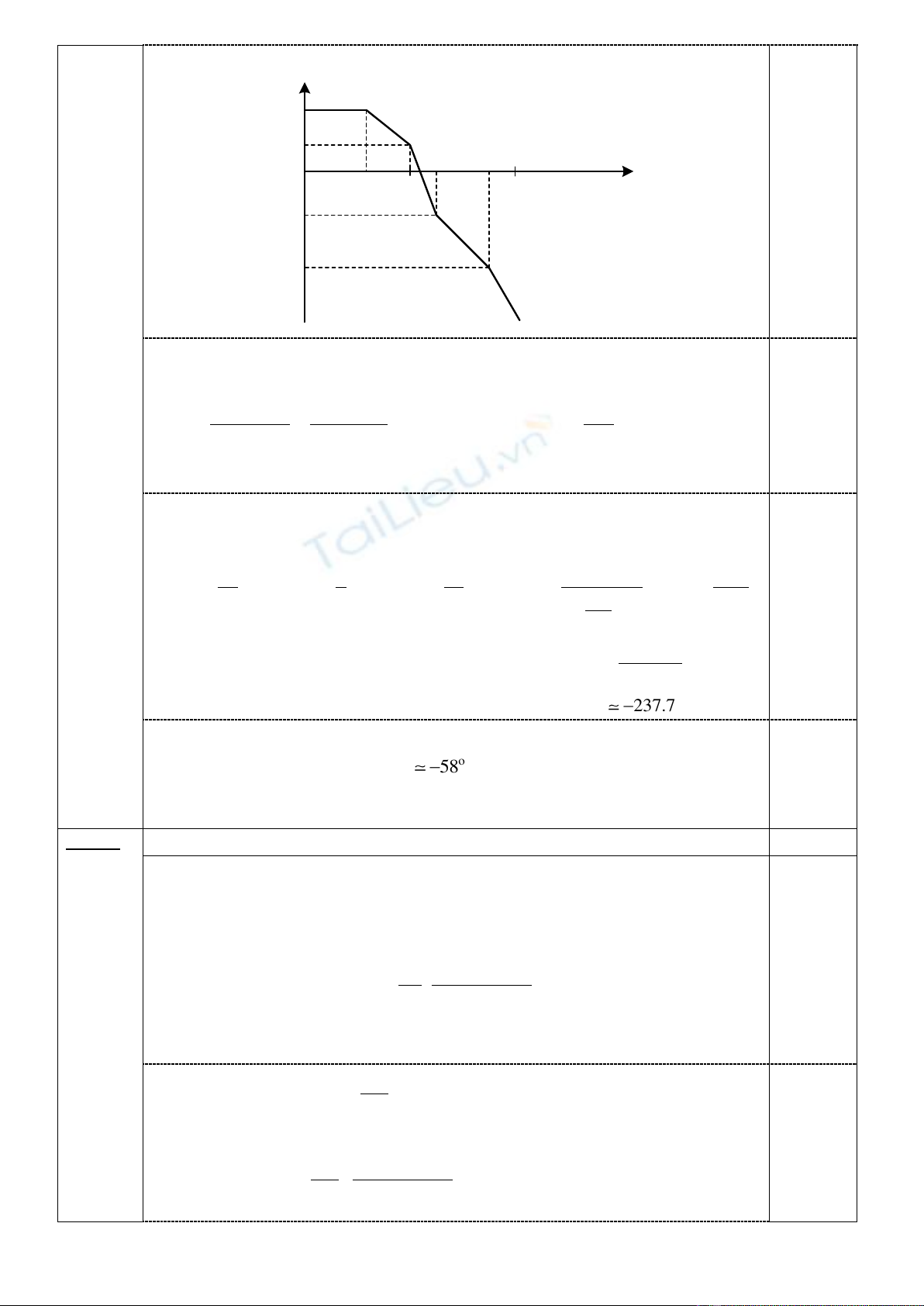
Hệ số khuếch đại chung: K=5
20lgK = 20lg10= 14 dB
Các tần số gãy: = 4, 10, 20,50[rad/s] tương ứng với
lg
= 0.6, 1, 1.3, 1.7
0.5
Gọi
4 10 20 50
L , L ,L ,L
là giá trị L tại các tần số = 4,10, 20, 50 [rad/s]
4
L 14(dB)
10 4
LL 20
lg10 lg4


10
L 14 20(1 0.6) 6(dB)
20 10
LL 60
lg20 lg10


20
L 6 60(1.3 1) 12(dB)
50 20
LL 40
lg50 lg20


50
L 12 40(1.7 1.3) 28(dB)
0.5
Biểu đồ Bobe:
1
Trang 3
-20 dB/dec
-60 dB/dec
-40 dB/dec
-60 dB/dec
lg
0.6 11.3 1.7
14
6
-12
-28
()L
dB
c (1.5đ). Xét ổn định của hệ kín:
Tính tần số cắt biên:
c 10
cc
LL 06 60
lg( /10) lg( /10)


c6
lg( /10) 0.1
60
Tần số cắt biên:
0.1
c10 10 12,6
[rad/s]
0,5
Tính góc pha tại tần số cắt biên:
(c)
0
c
c c c c
2
c
2
0.12
1 1 1 180
arctg arctg arctg arctg 0.1
1
20 4 50 110







(c)
0
1.512
arctg 0.63 arctg 3.15 arctg(0.252) arctg 72.2
0.5876



(c)
o o o o
32.2 72.4 14.14 (180 68.76 ) 72.2 237.78
0,75
Xét ổn định hệ kín
Độ dự trữ pha
o
c
PM 180 ( ) 58
< 0
Độ dự trữ pha nhỏ hơn không nên hệ kín không ổn định
0,25
CÂU 3
(3đ)
Đáp án
Điểm
a. Với bộ điều khiển PI, nên hàm truyền vòng hở của hệ có một khâu tích phân lý
tưởng. Do đó, khi tín hiệu vào là hàm nấc (step) hệ có sai số xác lập luôn bằng
0.
Hệ số sai số vận tốc:
I
vP
2
s 0 s 0
K100
K limsG(s)H(s) lims(K ) 100
ss 10s 100


I
K 100
0.5
0.5
b. KI = 100
cP
100
G (s) K s
Phương trình đặc trưng của hệ kín:
c
1 G (s)G(s) 0
P2
100 100
1 (K )( ) 0
ss 10s 100

Trang 4
32 P
s 10s 100(1 K )s 10000 0
0.5
Bảng Routh :
1
100(1+KP)
10
10000
100(1+KP)-1000
0
10000
Theo tiêu chuẩn Routh, điều kiện cần và đủ để hệ thống ổn định là các hệ số ở cột
thứ nhất của bảng Routh cùng dấu. Suy ra:
P
100(1 K ) 1000 0
P
K9
0.5
c. Sử dụng bộ điều khiển PD:
c P D
G (s) K K s
Hệ số sai số vị trí:
PD
2
s 0 s 0
100
K limG(s)H(s) lim(K K s)( ) 100
s 10s 100


P
K 100
Hàm truyền hệ kín:
cD
k2
cD
G (s)G(s) 100(100 K s)
G (s) 1 G (s)G(s) s 10s 100 100(100 K s)

D
k2D
100(100 K s)
G (s) s 10(1 10K )s 10100
Hàm truyền hệ kín có dạng khâu bậc 2 với:
- Tần số dao động riêng
2
nn
10100 100.5


(rad/s)
- Hệ số dao động riêng
, với
nD
2 10(1 10K )


Với
0.5
, suy ra:
n
D2 10
K 0.905
100


Vậy bộ điều khiển PD có dạng:
c
G (s) 100 0.905s
0.25
0.25
0.25
0.25
GV. Võ Lâm Chương