BÀI TẬP LỚN
BÀI TẬP LỚN
HỌC PHẦN :
HỌC PHẦN :TÍCH CỰC HÓA
TÍCH CỰC HÓA
QUÁ TRÌNH DẠY HỌC TOÁN
QUÁ TRÌNH DẠY HỌC TOÁN
Trần Thị Bích Như
Trần Thị Bích Như
Hoàng Thị Thanh Thủy
Hoàng Thị Thanh Thủy
Nguyễn Quí Hồng Phúc
Nguyễn Quí Hồng Phúc
Phạm Thành
Phạm Thành
Đ TÀI: NG D NG LÝ Ề Ứ Ụ
Đ TÀI: NG D NG LÝ Ề Ứ Ụ
THUY T KI N T O Đ D Y Ế Ế Ạ Ể Ạ
THUY T KI N T O Đ D Y Ế Ế Ạ Ể Ạ
H C ĐNH LÝ COSINỌ Ị
H C ĐNH LÝ COSINỌ Ị
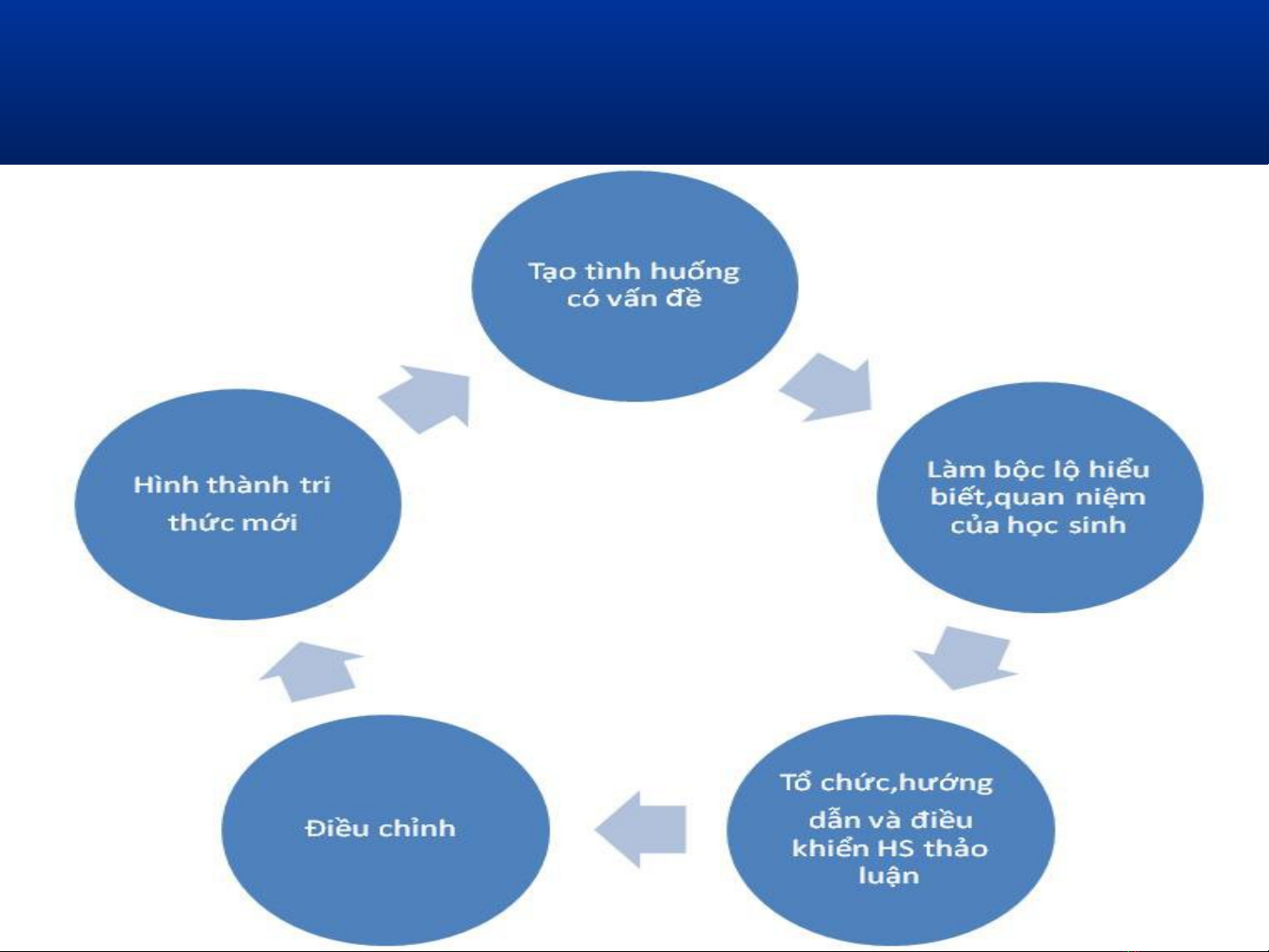
A. Mô hình d y h c c a lý thuy t ki n t o:ạ ọ ủ ế ế ạ
A. Mô hình d y h c c a lý thuy t ki n t o:ạ ọ ủ ế ế ạ
Trong quá trình d y h c toán có v n d ng lý thuy t ki n ạ ọ ậ ụ ế ế
Trong quá trình d y h c toán có v n d ng lý thuy t ki n ạ ọ ậ ụ ế ế
t o, thì chúng ta c n ph i xác đnh rõ m i quan h gi a ạ ầ ả ị ố ệ ữ
t o, thì chúng ta c n ph i xác đnh rõ m i quan h gi a ạ ầ ả ị ố ệ ữ
giáo viên và h c sinh, c th nh sau:ọ ụ ể ư
giáo viên và h c sinh, c th nh sau:ọ ụ ể ư
Nhi u nhà ki n t o trong quá trình d y h c đã th ng ề ế ạ ạ ọ ố
nh t quan đi m nh sau: HS h p tác v i nhau đ ti n ấ ể ư ợ ớ ể ế
hành các ho t đng nh n th c m t cách t giác, tích c c ạ ộ ậ ứ ộ ự ự
và sáng t o. Các nhà nghiên c u cũng ch ra r ng m i ạ ứ ỉ ằ ố
quan h th y áp đt – trò ph c tùng không th phát huy ệ ầ ặ ụ ể
đc tính đc l p và sáng t o c a ng i h c. Ng i h c ượ ộ ậ ạ ủ ườ ọ ườ ọ
không có đc h ng thú, s t tin và s tôn tr ng trong ượ ứ ự ự ự ọ
quá trình h c t p. ọ ậ
Ng c l i, h luôn th y gò bó, lo l ng. T ch c d y h c ượ ạ ọ ấ ắ ổ ứ ạ ọ
theo quan đi m c a lí thuy t ki n t o ng i GV c n xây ể ủ ế ế ạ ườ ầ
d ng đc m i quan h th y trò thân thi n, giúp HS t tin ự ượ ố ệ ầ ệ ự
và tho i mái. Trong ti n trình d y h c theo quan đi m c a lí ả ế ạ ọ ể ủ
thuy t ki n t o, vi c xác đnh rõ m i quan h th y trò là ế ế ạ ệ ị ố ệ ầ
h t s c quan tr ng. Đc bi t, ng i giáo viên ph i coi tr ng ế ứ ọ ặ ệ ườ ả ọ
nh ng ki n th c và kinh nghi m đã có c a ng i h c.ữ ế ứ ệ ủ ườ ọ