Trang 1/25 - Mã đề thi 188
TRƯỜNG THPT ………….
TỔ TOÁN
BÀI:………………….
NĂM HỌC 2018 – 2019
Môn: Toán - Lớp 11 - Chương trình chuẩn
ĐỀ CHÍNH THỨC Thời gian: ……… phút
Mã đề thi
188
Họ và tên:
………………………………………….
Lớp:
……………...……..………
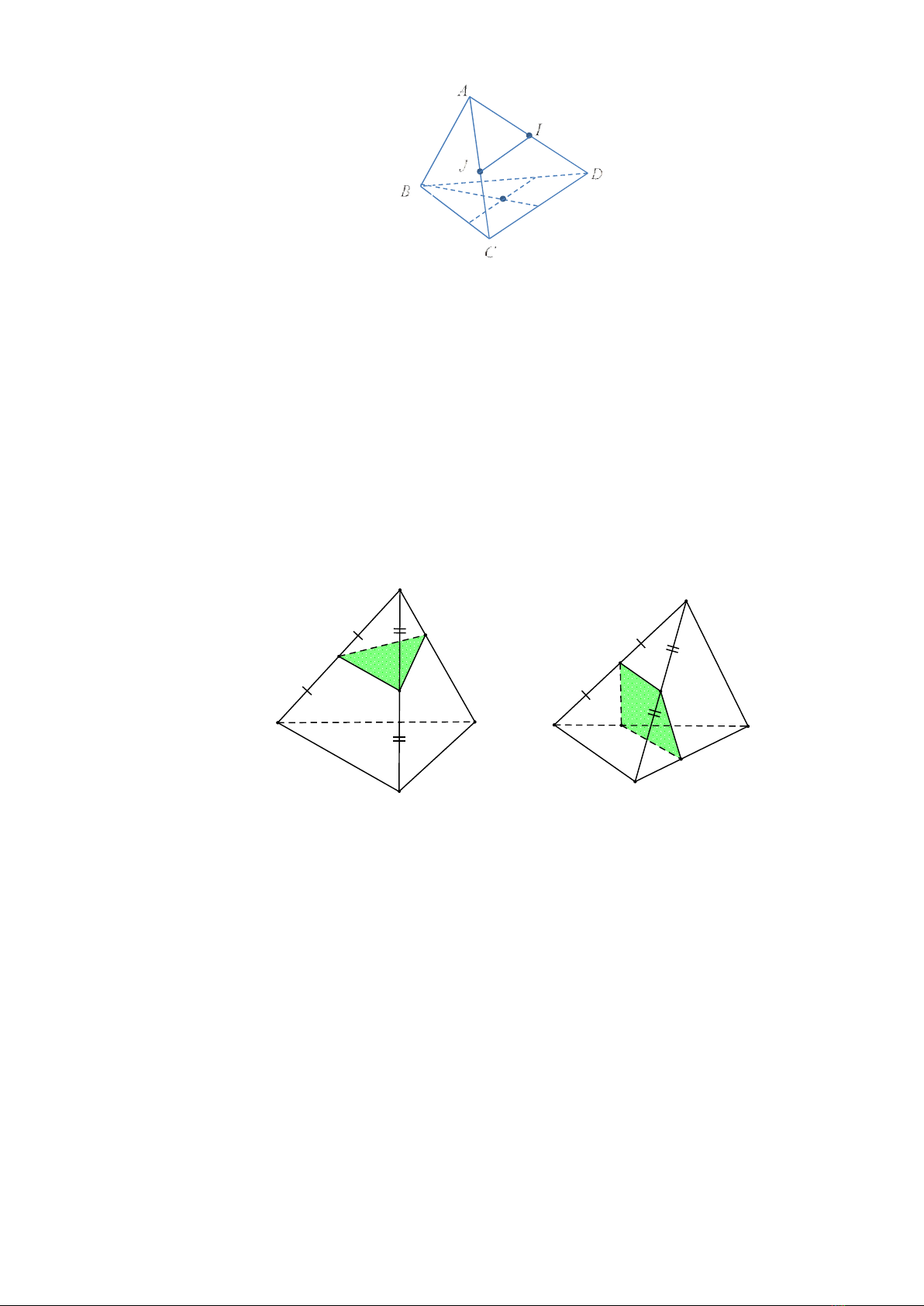
Câu 1. Cho tứ diện
ABCD
,
M
và
N
lần lượt là trung điểm
AB
và
AC
. Mặt phẳng
( )
qua
MN
cắt tứ
diện
ABCD
theo thiết diện là đa giác
Khẳng định nào sau đây đúng?
A.
T
là tam giác.
B.
T
là hình thoi.
C.
T
là tam giác hoặc hình thang hoặc hình bình hành.
D.
T
là hình chữ nhật.
Lời giải
Chọn C
qua
MN
cắt
AD
ta được thiết diện là một tam giác.
qua
MN
cắt hai cạnh
BD
và
CD
ta được thiết diện là một hình thang.
Đặc biệt khi mặt phẳng này đi qua trung điểm của
BD
và
CD
, ta được thiết diện là một hình bình
hành.
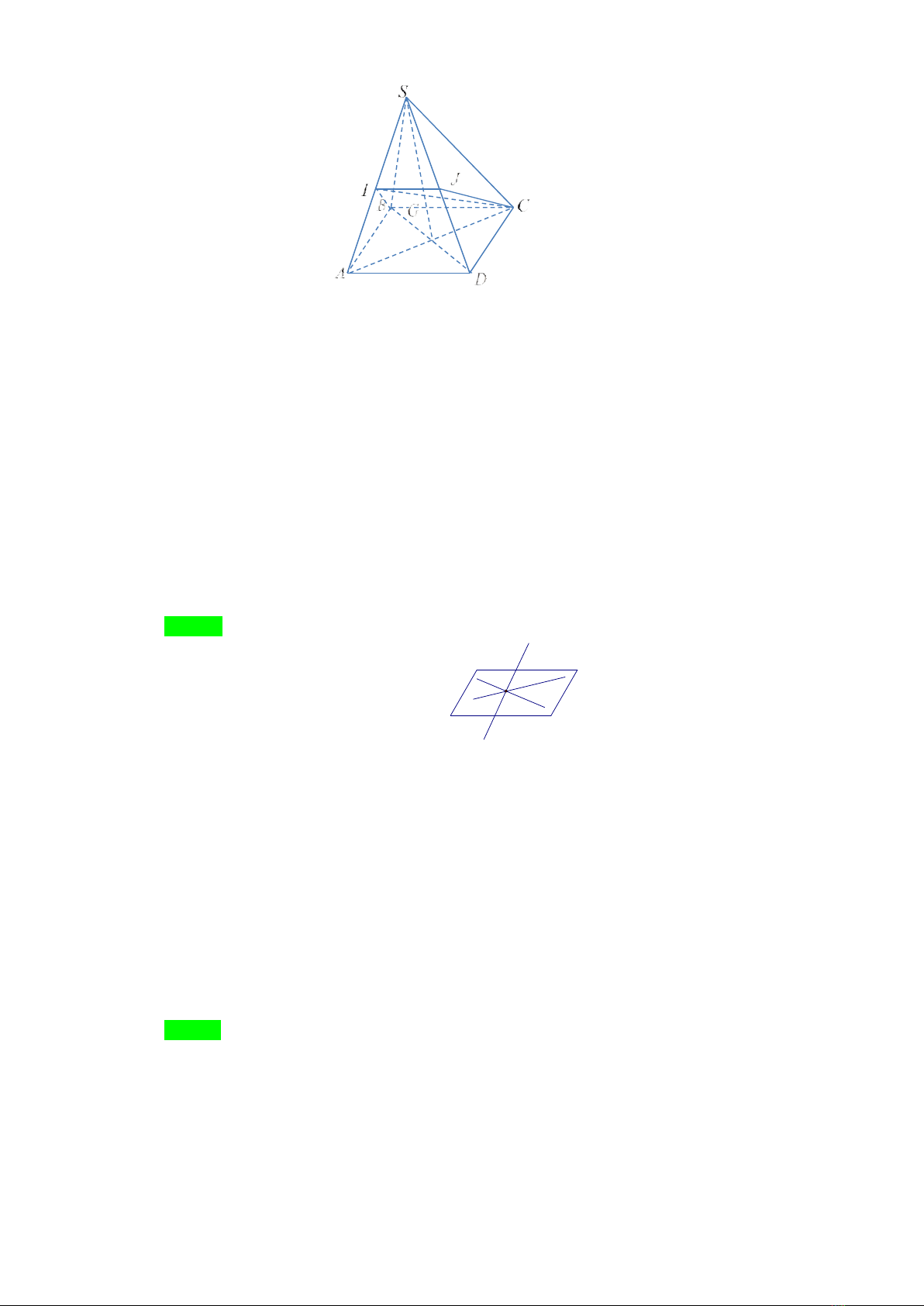
Câu 2. Cho tứ diện
ABCD
.
I
và
J
theo thứ tự là trung điểm của
AD
và
AC
,
G
là trọng tâm tam
giác
BCD
. Giao tuyến của hai mặt phẳng
GIJ
và
BCD
là đường thẳng:
A. qua
J
và song song với
.BD
B. qua
G
và song song với
.CD
C. qua
G
và song song với
.BC
D. qua
I
và song song với
.AB
Lời giải
Chọn B
Trang 2/25 - Mã đề thi 188
Gọi
d
là giao tuyến của
GIJ
và
BCD
.
Ta có
G GIJ BCD
,
//IJ CD
,
IJ GIJ
,
CD BCD
.
Suy ra
d
đi qua
G
và song song với
CD
.
Câu 3. Cho tứ diện
ABCD
,
M
và
N
lần lượt là trung điểm
AB
và
AC
. Mặt phẳng
qua
MN
cắt tứ
diện
ABCD
theo thiết diện là đa giác
.T
Khẳng định nào sau đây đúng?
A.
T
là tam giác.
B.
T
là hình thoi.
C.
T
là tam giác hoặc hình thang hoặc hình bình hành.
D.
T
là hình chữ nhật.
Lời giải
Chọn C
Trường hợp
AD K
T
là tam giác
.MNK
Do đó A và C sai.
Trường hợp
,BCD IJ
với
, ;I BD J CD
,I J
không trùng
.D
T
là tứ giác. Do đó B sai.
Câu 4. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
I
là trung điểm
SA
. Thiết diện của
hình chóp .
S ABCD
cắt bởi mặt phẳng
IBC
là:
A. Tam giác
.IBC
B. Hình thang
IJCB
(
J
là trung điểm
SD
).
C. Hình thang
IGBC
(
G
là trung điểm
SB
). D. Tứ giác
IBCD
.
Lời giải
N
M
N
M
B
C
D
A
A
D
C
B
I
J
K
Trang 3/25 - Mã đề thi 188
Chọn B
Gọi
O
là giao điểm của
AC
và
BD
,
G
là giao điểm của
CI
và
SO
.
Khi đó
G
là trọng tâm tam giác S
AC
. Suy ra
G
là trọng tâm tam giác
SBD
.
Gọi
J BG SD
. Khi đó
J
là trung điểm
SD
.
Do đó thiết điện của hình chóp cắt bởi
IBC
là hình thang
IJCB
(
J
là trung điểm
SD
).
Câu 5. (THPT Quảng Xương 1 - Thanh Hóa- Lần 1- 2017 - 2018 - BTN) Trong không gian cho hai
đường thẳng
a
và
b
cắt nhau. Đường thẳng
c
cắt cả hai đường thẳng
a
và
.b
Có bao nhiêu mệnh
đề sai trong các mệnh đề sau
(I)
a
,
b
,
c
luôn đồng phẳng.
(II)
a
,
b
đồng phẳng.
(III)
a
,
c
đồng phẳng.
A.
2
. B.
3
. C.
0
. D.
1
.
Lời giải
Chọn D
(I) là mệnh đề sai vì khi
a
,
b
,
c
đồng quy thì có thể không đồng phẳng.
(II), (III) là các mệnh đề đúng vì hai đường thẳng cắt nhau xác định một mặt phẳng.
Câu 6. Trong các mệnh đề sau đây, mệnh đề nào đúng?
A. Hai đường thẳng chéo nhau thì không có điểm chung.
B. Hai đường thẳng phân biệt không song song thì chéo nhau.
C. Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau.
D. Hai đường thẳng không có điểm chung thì chéo nhau.
Lời giải
Chọn A
Câu 7. Cho hình lăng trụ .
ABC A B C
. Gọi
,
M M
lần lượt là trung điểm của
BC
và
B C
.
,
G G
lần lượt
là trọng tâm tam giác
ABC
và
A B C
. Bốn điểm nào sau đây đồng phẳng?
A.
, , ,
A G M C
. B.
, , ,
A G M G
. C.
, , ,
A G G C
. D.
, , ,
A G M B
.
Lời giải
Chọn B
c
b
a
Trang 4/25 - Mã đề thi 188
MM
là đường trung bình trong hình bình hành
BB C C
nên
; // //
MM BB AA MM BB AA
Do đó
AA M M
là hình bình hành hay 4 điểm
, , ,
A G M G
đồng phẳng.
Câu 8. (Chuyên Phan Bội Châu - Nghệ An - Lần 1 - 2017 - 2018 - BTN) Cho hình chóp
.S ABCD
có
đáy
ABCD
là hình bình hành. Gọi
M
là trung điểm
SD
,
N
là trọng tâm tam giác
SAB
. Đường
thẳng
MN
cắt mặt phẳng
SBC tại điểm
I
. Tính tỷ số
IN
IM
.
A.
1
2
. B.
2
3
. C.
3
4
. D.
1
3
.
Lời giải
Chọn B
Gọi
;J E
lần lượt là trung điểm
;SA AB
.
Trong mặt phẳng
BCMJ gọi
I MN BC
.
฀ Ta có:
IM
là đường trung tuyến của tam giác
SID
.
฀ Trong tam giác
ICD
ta có
BE
song song và bằng
1
2CD
nên suy ra
BE
là đường trung bình của
tam giác
ICD E
là trung điểm
ID SE
là đường trung tuyến của tam giác
SID
.
Ta có:
N IM SE N
là trọng tâm tam giác
2
3
IN
SID IM
.
Câu 9. Cho hình bình hành
ABCD
và một điểm
S
không nằm trong mặt phẳng
ABCD . Giao tuyến của
hai mặt phẳng
SAB và
SCD là một đường thẳng song song với đường thẳng nào sau đây?
A.
AB
. B.
AC
. C.
BC
. D.
SA
.
Lời giải
Chọn A
Trang 5/25 - Mã đề thi 188
Xét
SAB
và
SCD
có
S
là điềm chung
//AB CD
AB SAB
CD SCD
// //SAB SCD Sx AB CD
Câu 10. Cho hình chóp
.S ABCD
có
AD
không song song với
BC
. Gọi
, ,M N
, , ,P Q R T
lần lượt là trung điểm
, , , , ,AC BD BC CD SA SD
. Cặp đường thẳng nào sau đây song song với nhau?
A.
MN
và
RT
. B.
PQ
và
RT
. C.
MP
và
RT
. D.
MQ
và
RT
.
Lời giải
Chọn D
Ta có:
,M Q
lần lượt là trung điểm của
,AC CD
MQ
là đường trung bình của tam giác
1
CAD MQ AD
Ta có:
,R T
lần lượt là trung điểm của
,SA SD
RT
là đường trung bình của tam giác
2
SAD RT AD
Từ
1 , 2
suy ra:
.MQ RT
x
A
B
D
C
S
T
R
Q
P
N
M
S
C
B
D
A