TRƯỜNG ĐẠI HỌC KINH TẾ TPHCM
KHOA TÀI CHÍNH DOANH NGHIỆP
MÔN TÀI CHÍNH HÀNH VI

Giảng đường TC123K36
GIẢI BÀI TẬP
TÀI CHÍNH HÀNH VI
Chương 1:
LÝ THUYẾT HỮU DỤNG KỲ VỌNG
Câu 1:
a. Triển vọng và phân phối xác suất.
Triển vọ .
Phân phối xác su t là qui luật cho bi t xác su t
ố 1 kho ng giá tr ố
) của tập số thực.
b.Rủi ro và sự không chắc chắn
Rủ ể ủ ố n bi t các
k t qu là gì và ứng với m i k t qu xác su t là bao nhiêu. Rủi ro có thể
ơ c b ng xác su t.
Sự không chắc chắn x y ra khi b n không thể tính toán, phân chia các xác su t
x y ra các k t qu , kể c khi có m t danh sách các k t qu có thể x y ra. Sự
không chắc chắn thì không thể c.
c.Hàm hữu dụng và hữu dụng kỳ vọng
ể ứ ớ ứ
ố ớ ự .
ọ ể ứ ứ ớ ể ọ
ớ ọ ọ ố ứ ớ ứ
ọ
Hàm h u d ọng: U= pr x u1 + (1-pr) x u2..
d.Ngại rủi ro, tìm kiếm rủi ro và thờ ơ rủi ro
Ng i rủ ự ắ ắ . M i rủi ro s có hàm h u d
E P > U P Đ ều này hàm ý r ng mức h u d ng của giá tr kỳ
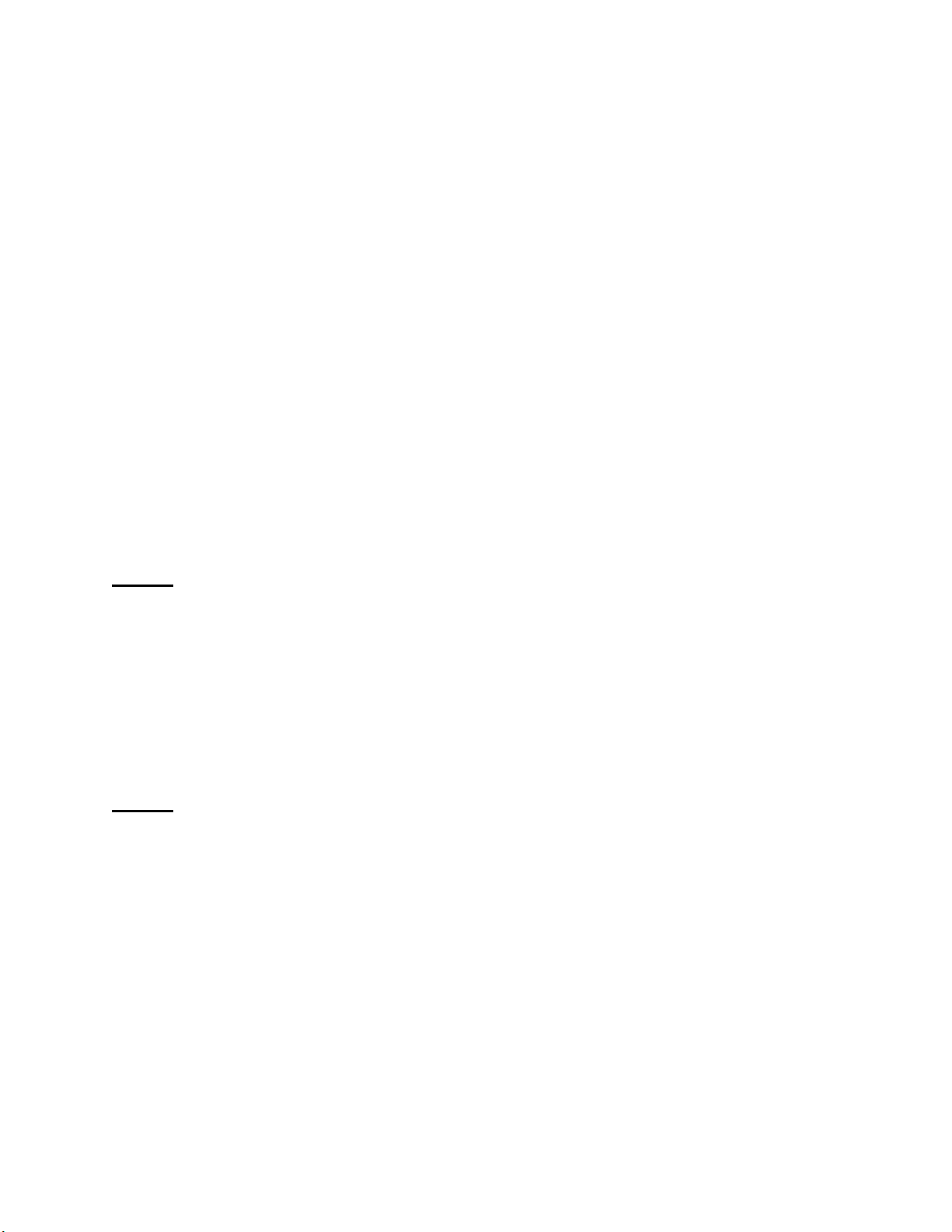
vọ ủ ển vọng thì lớ ơ ức h u d ng kỳ vọng của triển vọ
i này s thích giá tr kỳ vọng của triển vọ è ới sự chắc chắn
ơ c có m t k t qu không chắc chắn.
Tìm ki m rủ ủ c với nh i ng i rủi ro, m
m rủi ro s có hàm h u d U E P < U P Đ ều này hàm ý
r ng mức h u d ng của giá tr kỳ vọ ủ ể ọ ỏ ơ ức h u
d ng kỳ vọng của triển vọ i này s thích m o hiểm với m ò ơ ới
k t qu không chắc chắ ơ kỳ vọng của triển vọng chắc chắn.
Th ơ ủi ro:m cá nhân b coi là th ơ ới rủi ro s có d
U E P = U P Đ ều này hàm ý r ng mức h u d ng của giá tr kỳ vọng của
triển vọng s b ng mức h u d ng kỳ vọng của triển vọng. Nh i này chỉ
n giá tr kỳ vọ ủi ro không ph i v ề quan trọng.
Câu 2:
ắ ứ ự ứ )
P > > ố + phomat > hamburger.
ể ơ
ự ự ọ ủ ò ỏ ắ ự ự ọ
ủ ớ .
Câu 3:
a. Giá tr giàu có kỳ vọng củ i này
E(P)= 0.4*50000 + 1000000*0.6 = 620000.
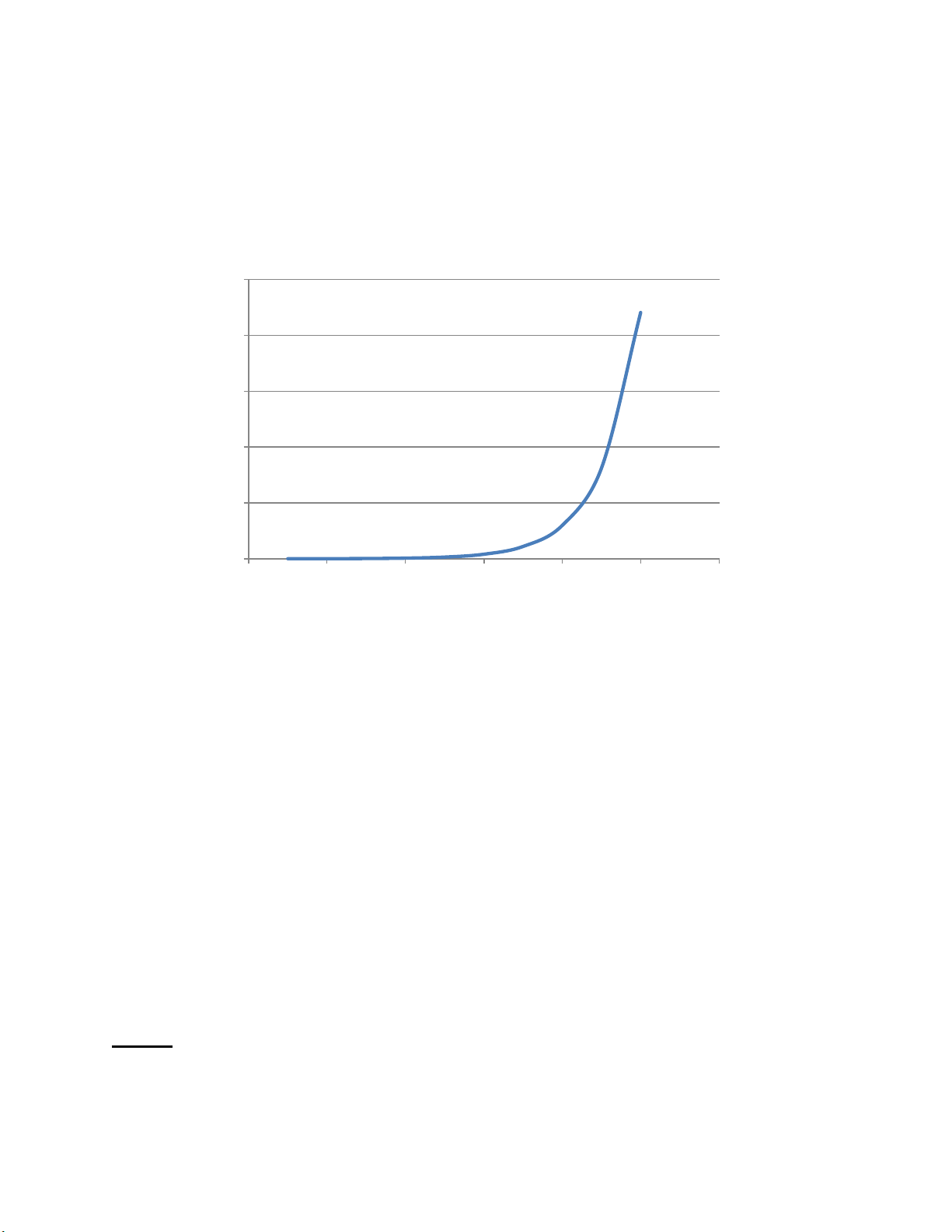
Đ th hàm h u d ng u(w)=ew
c. Ta có:
ủ .
ể P Đơ 100000.
U(P)=0.40*u(0.5) +0.60*u(10) =0.40*(e0.5) +0.6*(e10) = 13216.5
U(E(P)) =u(6.2)= e6.2 = 492.749
U P > U E w => i này tìm ki m rủi ro
d. Ta có U(w) = U(P) = 13216.5
ew = 13216.5
w =9 8922 ơ ơ ới 948922 $)
Sự ơ ơ ắc chắn củ i này ứng với triển vọng trên là 948922 $
Câu 4: u(w)=w0.5
a. Ta có
0
5000
10000
15000
20000
25000
0 2 4 6 8 10 12
U(P1)=0.8*u(1000)+0.2*u(600) =30.197
U(P2)=0.7*u(1200)+0.3*u(600)=31.597
U(P3)=0.5*u(2000)+0.5*u(300)=31.02
Dựa theo số li c ta có thể sắp x p thứ tự các triển vọ P
P2>P3>P1 (theo thứ tự từ t)
b. Ta có U(w)=U(P2)=31.597
w0.5=31.597
w=998.37
Vậy giá tr ơ ơ ắc chắn ứng với triển vọng P2 là 998.37
c. ủ => ủ =>
ơ ơ ắ ắ < ọ ủ ể ọ .
Câu 5:
ấ 1:
U(A) < U(B)
0.33*u(2500) + 0.66*u(2400) + 0.01*u(0) < u(2400)
0.33*u(2500) + 0.01*u(0) < 0.34*u(2400) (1)
ấ 2:
U(C) > U(D)
0.33*u(2500) + 0.67*u(0) > 0.34*u(2400) + 0.66*u(0)
0.33*u(2500) + 0.01*u(0) > 0.34*u(2400) (2)
2 => ớ ọ
ủ ố ứ ớ
ủ ậ ỏ
ủ .