
C NG HOÀ XÃ H I CH NGHĨA VI T NAMỘ Ộ Ủ Ệ
Đc l p - T do - H nh phúcộ ậ ự ạ
ĐN YÊU C U CÔNG NH N SÁNG KI NƠ Ầ Ậ Ế
Kính g i:ử H i đng th m đnh sáng ki n phòng GD&ĐT huy n Hoa ộ ồ ẩ ị ế ệ
L ;ư
Tôi ghi tên d i đây:ướ
H và tênọ
Ngày
tháng
năm sinh
N i công tácơ
(ho c n i cặ ơ ư
trú)
Ch cứ
danh
Trình
độ
chuyên
môn
T l %ỷ ệ
đóng góp
vào vi cệ
t o raạ
sáng
ki nế
Võ Th H ngị ồ 05/6/1980 P.Nam Thành-
TP. Ninh Bình
Giáo
viênĐi h cạ ọ 100%
I. Tên sáng ki n, lĩnh v c áp d ng: ế ự ụ
- Tên sáng ki n: “M t s gi i pháp giúp h c sinh l p 9 gi i bài t p ế ộ ố ả ọ ớ ả ậ
V t lý nâng cao ph n đi n h c”ậ ầ ệ ọ
- Lĩnh v c áp d ng: ự ụ Lĩnh v c Giáo d cự ụ
II. N i dungộ
1. Gi i pháp cũ th ng làmả ườ
Ph n đi n h c các giáo viên d y các em theo t ng ch đ theo các ti t h c trongầ ệ ọ ạ ừ ủ ề ế ọ
sách giáo khoa, t ki n th c c a bài tôi đa ra bài t p t d đn khó. C th : ừ ế ứ ủ ư ậ ừ ễ ế ụ ể
D ng 1: Đnh lu t Ôm.ạ ị ậ
D ng 2: Đnh lu t Ôm đi v i đo n m ch n i ti p.ạ ị ậ ố ớ ạ ạ ố ế
D ng 3: Đnh lu t Ôm đi v i đo n m ch song song.ạ ị ậ ố ớ ạ ạ
D ng 4: Đnh lu t Ôm đi v i đo n m ch h n h p.ạ ị ậ ố ớ ạ ạ ỗ ợ
D ng 5: Đi n tr dây d n.ạ ệ ở ẫ
D ng 6: Bi n tr .ạ ế ở
D ng 7: Công- Công su t.ạ ấ

D ng 8: Đnh lu t Jun-Len x .ạ ị ậ ơ
V i m i d ng, giáo viên cung c p cho các em ki n th c c b n (ch y uớ ỗ ạ ấ ế ứ ơ ả ủ ế
là công th c áp d ng) r i đa ra bài t p t d đn khó, yêu c u các em tìm cáchứ ụ ồ ư ậ ừ ễ ế ầ
gi i. Có nh ng bài h c sinh không làm đc thì giáo viên l i h ng d n cho cácả ữ ọ ượ ạ ướ ẫ
em nh ng ch a rút ra bài h c hay ph ng pháp cho m i d ng bài. Có nh ng bàiư ư ọ ươ ỗ ạ ữ
ph i s d ng đn các công th c toán h c thì giáo viên l i cung c p cho các emả ử ụ ế ứ ọ ạ ấ
đ áp d ng vào bài. ể ụ
V i cách làm này tôi nh n th y có nh ng u đi m và h n ch sau:ớ ậ ấ ữ ư ể ạ ế
1.1. u đi m c a gi i pháp cũ Ư ể ủ ả
V i nh ng bài t p c b n, h c sinh đc cung c p công th c nên v nớ ữ ậ ơ ả ọ ượ ấ ứ ậ
d ng t ng đi t t. Các d ng bài tôi đa ra cũng đc phân theo các bài tr ngụ ươ ố ố ạ ư ượ ọ
tâm theo sách giáo khoa, vì th h c sinh n m đc công th c và cách gi i t ngế ọ ắ ượ ứ ả ừ
d ng bài.ạ
1.2. T n t i, h n ch c a gi i pháp cũ ồ ạ ạ ế ủ ả
- H c sinh không t phân lo i đc bài t p, vi c phân lo i và ph ngọ ự ạ ượ ậ ệ ạ ươ
pháp gi i cho t ng d ng cũng ch a linh ho t và sáng t o. ả ừ ạ ư ạ ạ
- T m i d ng tôi ch a rút ra kinh nghi m hay ph ng pháp cho các em từ ỗ ạ ư ệ ươ ư
duy nhanh h n, gi i quy t bài toán nhanh h n hay thông minh h n. ơ ả ế ơ ơ
- Ph n ki n th c toán h c b sung cho các em ch a k p th i, đn bài nàoầ ế ứ ọ ổ ư ị ờ ế
c n s d ng ki n th c toán thì tôi m i b sung cho các em d n đn các em chầ ử ụ ế ứ ớ ổ ẫ ế ỉ
nh máy m c cách làm bài mà ch a v n d ng đc trong các bài khác. ớ ọ ư ậ ụ ượ
- Cách phân lo i bài t p c a tôi ch a h p lí, còn thi u các d ng bài t pạ ậ ủ ư ợ ế ạ ậ
sáng t o, nâng cao h n. ạ ơ
- Do đó các em lúng túng khi gi i bài t p. V i nh ng ki n th c sách giáoả ậ ớ ữ ế ứ
khoa đa ra thì khi g p bài t p ph n đi n h c có d ng đc bi t ho c khôngư ặ ậ ầ ệ ọ ạ ặ ệ ặ
t ng minh, h c sinh không th tìm ra h ng gi i k t qu c a công tác b iườ ọ ể ướ ả ế ả ủ ồ
d ng h c sinh gi i trong nh ng năm tr c đây ch a cao.ưỡ ọ ỏ ữ ướ ư
Chính vì v y tôi m nh d n đa ra sáng ki n: ậ ạ ạ ư ế “M t s gi i pháp giúpộ ố ả
h c sinh l p 9 gi i bài t p V t lý nâng cao ph n đi n h c” ọ ớ ả ậ ậ ầ ệ ọ
2. Gi i pháp m i, c i ti nả ớ ả ế
Tr c tiên, giáo viên c n giúp h c sinh n m v ng ki n th c c b n c aướ ầ ọ ắ ữ ế ứ ơ ả ủ
ph n Đi n h c. Các công th c v t lý, đn v các đi l ng và cách bi n đi,ầ ệ ọ ứ ậ ơ ị ạ ượ ế ổ
v n d ng công th c sao cho phù h p v i t ng bài. Cung c p thêm cho các emậ ụ ứ ợ ớ ừ ấ
các ki n th c b tr nâng cao trong các tài li u tham kh o, tài li u b i d ngế ứ ổ ợ ệ ả ệ ồ ưỡ
h c sinh gi i.ọ ỏ

Chú tr ng hình thànhọ các năng l cự ( T h c; Gi i quy t v n đ; Sáng t o;ự ọ ả ế ấ ề ạ
H p tác; Tính toán ) ợ
Bên c nh đó giáo viên ph i giúp h c sinh nh l i và n m v ng đc cácạ ả ọ ớ ạ ắ ữ ượ
ki n th c v môn Toán b tr tr c khi đa ra bài t p. Cung c p cho h c sinhế ứ ề ổ ợ ướ ư ậ ấ ọ
nh ng ki n th c toán h c và nh ng th thu t r t c n thi t trong quá trình gi iữ ế ứ ọ ữ ủ ậ ấ ầ ế ả
bài t p v t lý (ph ng trình nghi m nguyên, tìm c c đi, c c ti u, tam th c b cậ ậ ươ ệ ự ạ ự ể ứ ậ
hai,…).
2.1. Gi i pháp 1: B tr các ki n th c toán h c c n thi t cho h c sinhả ổ ợ ế ứ ọ ầ ế ọ
V i bài toán khó thì kĩ năng toán h c là y u t quy t đnh thành công vàớ ọ ế ố ế ị
h c sinh c n ph i có nh ng kĩ năng sau:ọ ầ ả ữ
+ Kĩ năng đc hi u đ.ọ ể ề
+ Kĩ năng bi u di n hình minh h a đ bài (n u có).ể ễ ọ ề ế
+ Kĩ năng phân tích hi n t ng v t lý x y ra.ệ ượ ậ ả
+ Kĩ năng s d ng công th c (đnh lu t, đnh nghĩa, khái ni m, tínhử ụ ứ ị ậ ị ệ
ch t,...) ấ
+ Kĩ năng suy lu n (toán h c, lý h c,...) lôgic.ậ ọ ọ
+ Kĩ năng tính toán đ đi đn đáp s cu i cùng.ể ế ố ố
+ Kĩ năng bi n lu n.ệ ậ
Sau đây là m t s ki n th c Toán h c các em c n n m đc và v n d ngộ ố ế ứ ọ ầ ắ ượ ậ ụ
trong gi i bài t p V t lí:ả ậ ậ
2.1.1. H ph ng trình b c nh t nhi u n sệ ươ ậ ấ ề ẩ ố.
H ph ng trình d ng đi x ng.ệ ươ ạ ố ứ
D ng 1ạx + y = a (1)
y + z =b (2)
x + z = c (3)
( Cách gi i h ph ng trình d ng này ph n ph l c trang1 )ả ệ ươ ạ ở ầ ụ ụ
D ng 2: ạ z (y + x ) / ( x + y +z ) = a (1)
y ( x+ z) / ( x + y +z ) = b (2)
x (y + z ) / ( x + y +z ) = c (3)
( Cách gi i h ph ng trình d ng này ph n ph l c trang1)ả ệ ươ ạ ở ầ ụ ụ
Sau đây là hai ví d th c t khi h c sinh gi i bài t p v t lý th ng g pụ ự ế ọ ả ậ ậ ườ ặ
cho cách gi i này.ả
Ví d 1ụ: Cho h p đen nh v 1. V i các d ng c vôn k , ampe k , ngu nộ ư ẽ ớ ụ ụ ế ế ồ
đi n, dây n i và m t khoá K. B ng th c nghi m hãy xác đnh các đi n tr trongệ ố ộ ằ ự ệ ị ệ ở
h p.ộ
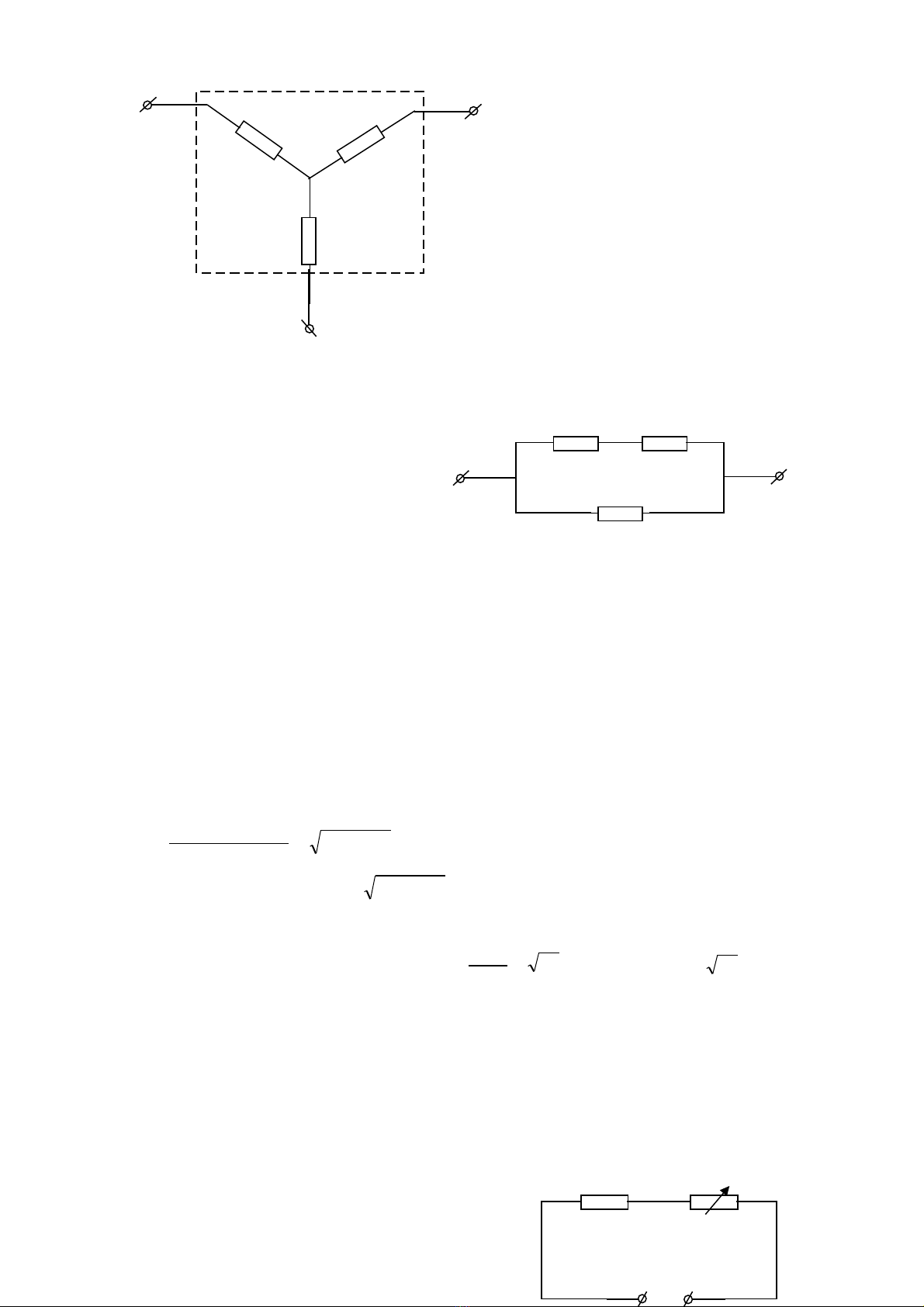
Hình 1
H ng d n cách gi iướ ẫ ả : Ph n Ph l c – Trang 2ầ ụ ụ
Ví d 2ụ: Cho m t m ch đi nộ ạ ệ
nh hình v . ư ẽ Bi t đi n tr c aế ệ ở ủ
đo n m ch là 8ạ ạ . N u thay đi vế ổ ị
trí R1 và R2 ta đc đi n tr đo nượ ệ ở ạ
m ch là 16ạ, n u thay đi v trí Rế ổ ị 1
và R3 ta đc đi n tr đo n m ch làượ ệ ở ạ ạ
10. Tính các đi n tr . ệ ở
Hình 2
H ng d n cách gi iướ ẫ ả : Ph n Ph l c – Trang3ầ ụ ụ
2.1.2. B t đng th cấ ẳ ứ
D ng này h c sinh th ng g p khi gi i bài toán v công su t c a dòngạ ọ ườ ặ ả ề ấ ủ
đi n, v bi n tr thay đi giá tr và tìm giá tr c c đi, c c ti u. ệ ề ế ở ổ ị ị ự ạ ự ể
*B t đng th c Cô si:ấ ẳ ứ
Cho a1, a2, ..., an là nh ng s không âm thì: ữ ố
nn
naaa
n
aaa ....
...
21
21
Hay:
nnn aaanaaa ....... 2121
D u “=” x y ra ấ ả
a1 = a2 = ...= an
Áp d ng v i 2 s a, b không âm, ta có: ụ ớ ố
ab
ba
2
hay: a + b
2
ab
D u “=” x y ra khi a = b.ấ ả
Trong các bài toán v t lý khi đa ra\đc l p lu n a = b thì gi i quy tậ ư ượ ậ ậ ả ế
r t nhi u v n đ liên quan.ấ ề ấ ề
2.1.3. S d ng nghi m c a ph ng trình b c hai: ử ụ ệ ủ ươ ậ
0
2
cbxax
Trong bài toán v t lý th ng là nh ng giá tr th t, nên bài toán luôn cóậ ườ ữ ị ậ
nghi m. Khi g p bài toán tìm giá tr c c đi ho c c c ti u ta l i d ng ệ ặ ị ự ạ ặ ự ể ợ ụ 0,
v i ớ
= b2 - 4ac
R1R2
R3
3
2
1
R2
R1
R3
R0
+ U -
Rx

Ví d 3: ụCho m ch đi n g mạ ệ ồ
1 bi n tr Rế ở x m c n i ti p v i 1ắ ố ế ớ
đi n tr Rệ ở 0 vào ngu n đi n có hi uồ ệ ệ
đi n th không đi U. Tìm giá tr Rệ ế ổ ị x
đ công su t tiêu th trên nó là l nể ấ ụ ớ
nh t?ấ
Hình 3
Cách 1: Dùng phép bi n điế ổ
Nguyên t c chung khi kh o sát m t đi l ng theo giá tr bi n đi, thì ắ ả ộ ạ ượ ị ế ổ t tố
nh t nên hình thành bi u th c c a đi l ng kh o sát theo giá tr bi n điấ ể ứ ủ ạ ượ ả ị ế ổ
đ gi i quy t.ể ả ế
Cách 2: Dùng b t đng th c đ gi iấ ẳ ứ ể ả
Cách 3: Gi i theo ph ng trình b c hai v i n là Pả ươ ậ ớ ẩ x
H ng d n cách gi iướ ẫ ả : Ph n Ph l c – Trang 3ầ ụ ụ
2.2. Gi i pháp th hai: Phân lo i và hả ứ ạ ng d n gi i các d ng bài t pướ ẫ ả ạ ậ
theo t ng d ngừ ạ
2.2.1. Lo i m ch đi n t ng đng - Các quy t c chuy n m ch.ạ ạ ệ ươ ươ ắ ể ạ
Ch y u c a ph n này là hình thành m ch đi n t ng đng, tính đi nủ ế ủ ầ ạ ệ ươ ươ ệ
tr theo các đi n tr thành ph n và m t s m ch đc bi t khác:ở ệ ở ầ ộ ố ạ ặ ệ
*Ph ng pháp: ươ
- D a theo các tính ch t c a đo n m ch n i ti p, song song trong ch ngự ấ ủ ạ ạ ố ế ươ
trình V t lý THCS.ậ
- Các th thu t khác (th thu t bi n đi t ng đng, ch p m ch, bủ ậ ủ ậ ế ổ ươ ươ ậ ạ ỏ
đi n tr , ghép đi n tr ,…). Đc bi t ph n này tôi đi sâu vào các kinh nghi mệ ở ệ ở ặ ệ ầ ệ
dùng th thu t đ gi i các bài t p (các d ng bài t p mà không th áp d ng cácủ ậ ể ả ậ ạ ậ ể ụ
tính ch t thông th ng c a đo n m ch đ gi i quy t đc).ấ ườ ủ ạ ạ ể ả ế ượ
- Toán h c h tr ph n bài t p này là ph ng trình nghi m nguyên (2 n,ọ ổ ợ ầ ậ ươ ệ ẩ
3 n) và ph ng trình b c hai.ẩ ươ ậ
- T ng bài toán s rút cho h c sinh bi t đi m c b n và th thu t gi iừ ẽ ọ ế ể ơ ả ủ ậ ả
quy t. ế
Tóm l iạ: Bài toán tính đi n tr toàn m ch d a trên các đi n tr thànhệ ở ạ ự ệ ở
ph n d a theo các qui t c sau:ầ ự ắ
a. Qui t c bi n đi t ng đngắ ế ổ ươ ươ d a trên các tính ch t c b n c aự ấ ơ ả ủ
đo n m ch m c n i ti p, m c song song (đo n m ch thu n tuý song song,ạ ạ ắ ố ế ắ ạ ạ ầ
thu n tuý n i ti p hay h n h p c a song song và n i ti p) ầ ố ế ỗ ợ ủ ố ế
b. Qui t c ch p m ch các đi m có cùng đi n thắ ậ ạ ể ệ ế :


























