
1. M ĐUỞ Ầ
1.1. Lí do ch n đ tàiọ ề
Trong chưng trình Toán l p 11 hi n nay, ph n hình h c không gian làmơ ớ ệ ầ ọ
cho ph n l n h c sinh đu c m th y chán n n, khó hi u khi ti p xúc v i mônầ ớ ọ ề ả ấ ả ể ế ớ
h c đòi h i nhi u k năng và t duy tr u t ng cao này. M t trong nh ng khóọ ỏ ề ỹ ư ừ ượ ộ ữ
khăn mà h c sinh hay g p ph i là s khác nhau gi a hình ph ng và hình h cọ ặ ả ự ữ ẳ ọ
không gian. Khi xét v quan h vuông góc và các bài toán liên quan, đi v i hìnhề ệ ố ớ
h c ph ng, hình v mang tính tr c quan, hai đng th ng vuông góc thì c tọ ẳ ẽ ự ườ ẳ ắ
nhau. Nh ng đi v i các bài toán v quan h vuông góc trong không gian, h cư ố ớ ề ệ ọ
sinh ph i d a trên các đnh nghĩa, đnh lí và hình bi u di n đ tìm l i gi i nênả ự ị ị ể ễ ể ờ ả
h c sinh g p r t nhi u khó khăn. M t trong các bài toán quan tr ng v quan họ ặ ấ ề ộ ọ ề ệ
vuông góc trong không gian là bài toán v kho ng cách, nó xu t hi n h u h tề ả ấ ệ ở ầ ế
các đ thi tuy n sinh vào đi h c, cao đng, đ thi h c sinh gi i và đ thi THPTề ể ạ ọ ẳ ề ọ ỏ ề
qu c gia trong nh ng năm g n đây. M c dù v y, đây l i là ph n ki n th c đòiố ữ ầ ặ ậ ạ ầ ế ứ
h i h c sinh ph i có t duy sâu s c, có trí t ng t ng hình không gian phongỏ ọ ả ư ắ ưở ượ
phú, có kh năng t ng h p ki n th c c v quan h song song l n quan hả ổ ợ ế ứ ả ề ệ ẫ ệ
vuông góc trong không gian, c v các bài toán đnh tính, đnh l ng trong hìnhả ề ị ị ượ
h c ph ng. Xu t phát t nh ng lí do trên tôi l a ch n đ tài sáng ki n kinhọ ẳ ấ ừ ữ ự ọ ề ế
nghi m: “ệGiúp h c sinh l p 11 tính kho ng cách t m t đi m đn m t m tọ ớ ả ừ ộ ể ế ộ ặ
ph ng b ng cách tìm hình chi u c a m t đi m lên m t m t ph ng”.ẳ ằ ế ủ ộ ể ộ ặ ẳ
1.2. M c đích nghiên c uụ ứ
Qua th c t gi ng d y, v i m t s năm kinh nghi m, tôi đã rút ra đc m tự ế ả ạ ớ ộ ố ệ ượ ộ
s kinh nghi m nh trong vi c h ng d n, giúp h c sinh gi i các bài toán tínhố ệ ỏ ệ ướ ẫ ọ ả
kho ng cách t m t đi m đn m t m t ph ng và kho ng cách gi a hai đngả ừ ộ ể ế ộ ặ ẳ ả ữ ườ
th ng chéo nhau. M t thao tác h t s c quan tr ng mà h c sinh c n ph i có đó làẳ ộ ế ứ ọ ọ ầ ả
xác đnh đúng hình chi u c a m t đi m lên m t m t ph ng cho tr c. Vì v y,ị ế ủ ộ ể ộ ặ ẳ ướ ậ
trong bài vi t này, tôi t p trung vào vi c giúp h c sinh xác đnh hình chi u c aế ậ ệ ọ ị ế ủ
m t đi m lên m t m t ph ng t đó tính đc kho ng cách t m t đi m đnộ ể ộ ặ ẳ ừ ượ ả ừ ộ ể ế
m t m t ph ng và kho ng cách gi a hai đng th ng chéo nhau.ộ ặ ẳ ả ữ ườ ẳ
1.3. Đi t ng nghiên c uố ượ ứ
Trong đ tài này, đi t ng nghiên c u c a tôi là cách tìm hình chi u c aề ố ượ ứ ủ ế ủ
m t đi m lên m t m t ph ng.ộ ể ộ ặ ẳ
1.4. Ph ng pháp nghiên c uươ ứ
Trong quá trình nghiên c u tôi đã s d ng các ph ng pháp sau:ứ ử ụ ươ
- Ph ng pháp đi u tra giáo d c.ươ ề ụ
- Ph ng pháp quan sát s ph m.ươ ư ạ
- Ph ng pháp phân tích và t ng h p lý thuy t.ươ ổ ợ ế
- Ph ng pháp phân lo i và h th ng hóa lý thuy t.ươ ạ ệ ố ế
2. N I DUNG SÁNG KI N KINH NGHI MỘ Ế Ệ
2.1. C s lí lu nơ ở ậ
2.1.1. Kho ng cách t m t đi m đn m t m t ph ngả ừ ộ ể ế ộ ặ ẳ
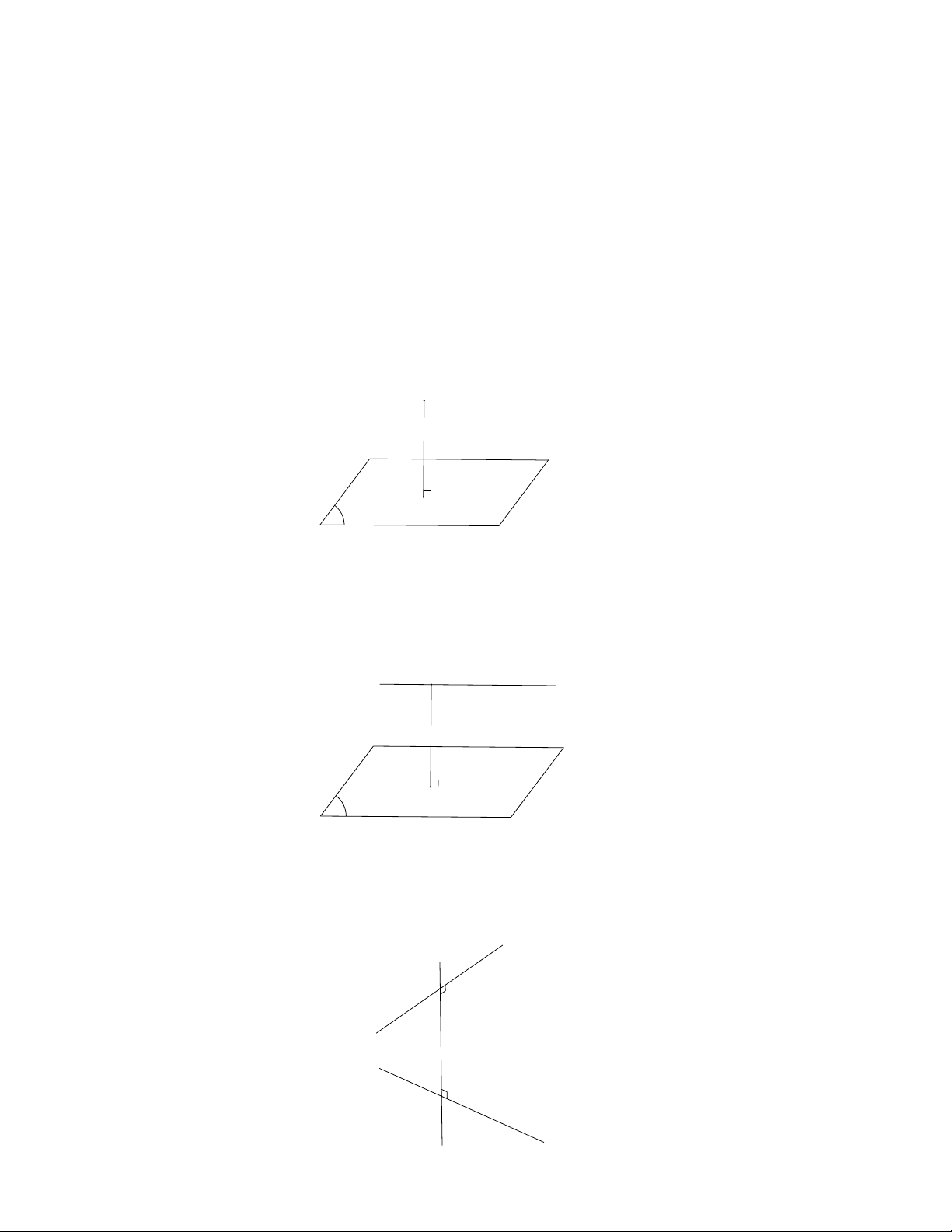
- Kho ng cách t đi m M đn m t ph ng (P) là kho ng cách gi a hai đi m Mả ừ ể ế ặ ẳ ả ữ ể
và H, trong đó H là hình chi u c a đi m M lên m t ph ng (P).ế ủ ể ặ ẳ
- Kho ng cách t M đn m t ph ng (P) đc kí hi u là: d(M; (P)) = MH.ả ừ ế ặ ẳ ượ ệ
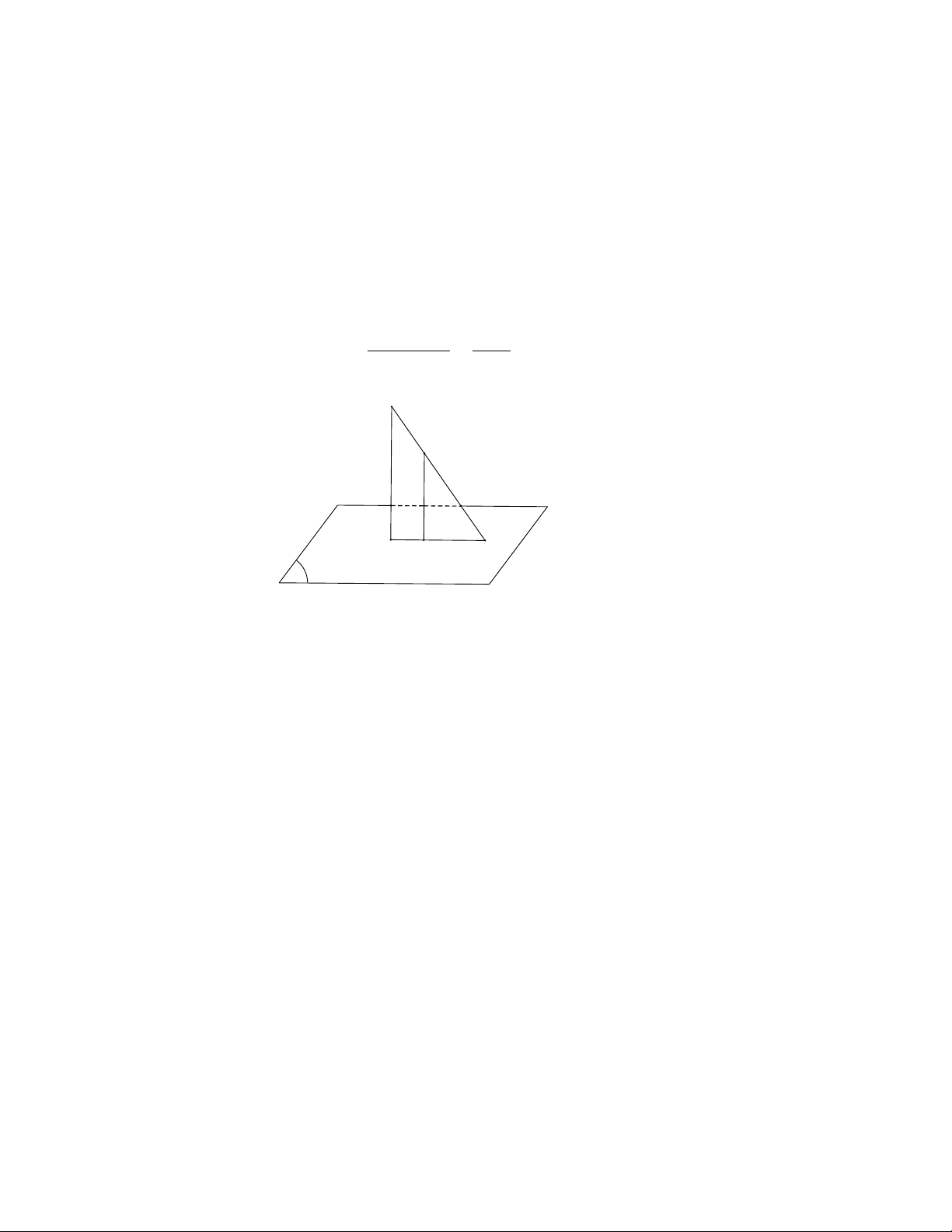
2.1.2. Kho ng cách gi a đng th ng và m t ph ng song songả ữ ườ ẳ ặ ẳ
- Kho ng cách gi a đng th ng a và m t ph ng (P) song song v i a là kho ngả ữ ườ ẳ ặ ẳ ớ ả
cách t m t đi m nào đó c a đng th ng a đn m t ph ng (P).ừ ộ ể ủ ườ ẳ ế ặ ẳ
- Kí hi u kho ng cách gi a đng th ng a và m t ph ng (P) song song v i nó là:ệ ả ữ ườ ẳ ặ ẳ ớ
d(a;(P)).
d(a,(P)) d(M,(P)) v i M a�=
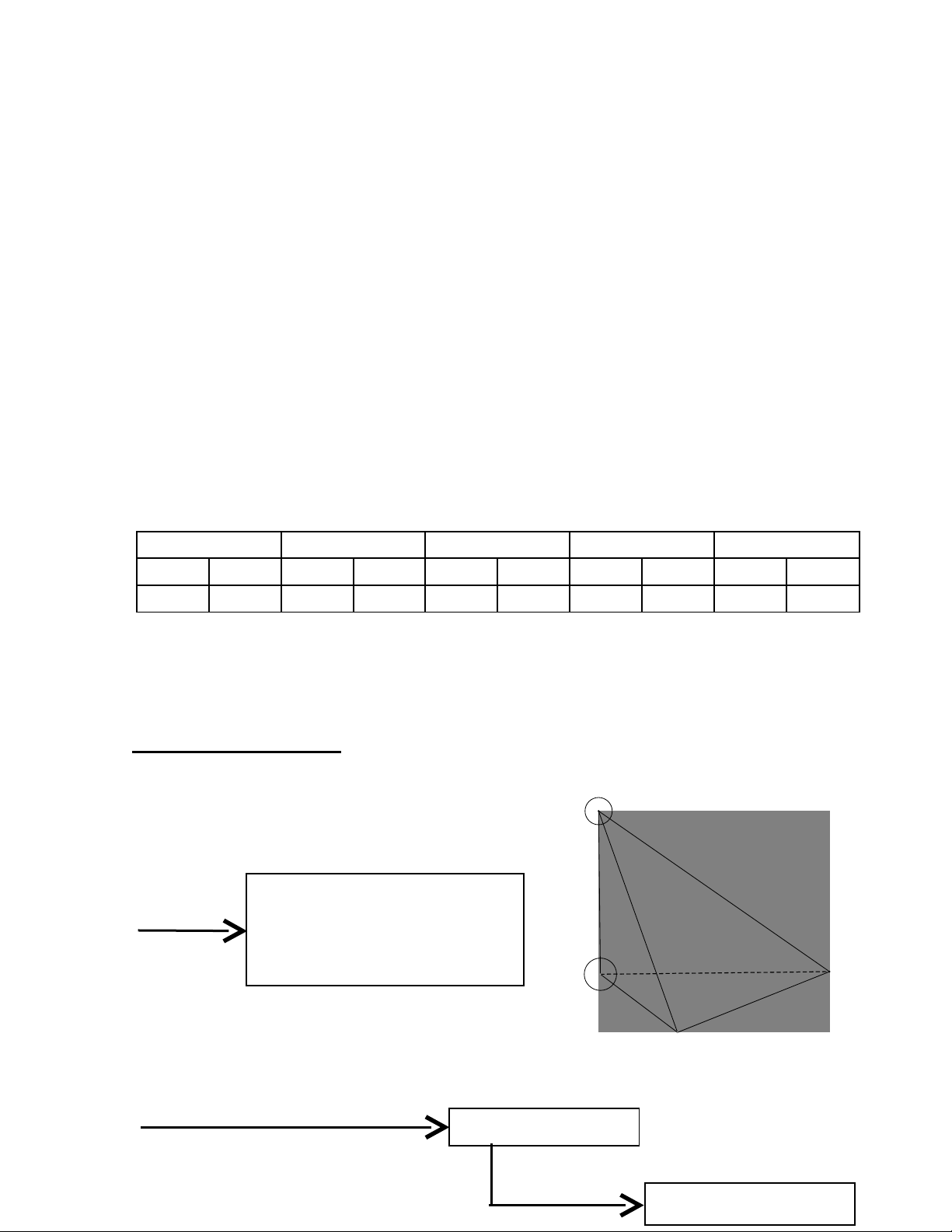
2.1.3. Kho ng cách gi a hai đng th ng chéo nhauả ữ ườ ẳ
- Kho ng cách gi a hai đng th ng chéo nhau là đ dài đo n vuông góc chungả ữ ườ ẳ ộ ạ
c a hai đng th ng đó.ủ ườ ẳ
a
b
N
M
P
M
H
a
P
M
H
d(a,b) = MN
2.1.4. M t s nh n xétộ ố ậ
- Kho ng cách gi a hai đng th ng chéo nhau b ng kho ng cách gi a m t ả ữ ườ ẳ ằ ả ữ ộ
trong hai đng th ng đó và m t ph ng song song v i nó, ch a đng th ng cònườ ẳ ặ ẳ ớ ứ ườ ẳ
l i.ạ
- N u ế
{ }
MI (P) N=�
thì
d(M,(P)) MN
d(I,(P)) IN
=
.
2.2. Th c tr ng v n đ tr c khi áp d ng sáng ki n kinh nghi mự ạ ấ ề ướ ụ ế ệ
Th c tr ng d y h c hình h c không gian l p 11 nói chung và bài kho ngự ạ ạ ọ ọ ớ ả
cách nói riêng tr ng THPT đc th hi n m t s đi m sau:ở ườ ượ ể ệ ở ộ ố ể
Th nh t: Đi v i giáo viên, đ giúp h c sinh n m v ng đc lý thuy t vàứ ấ ố ớ ể ọ ắ ữ ượ ế
v n d ng đc lý thuy t vào gi i quy t các bài toán v kho ng cách thì th ngậ ụ ượ ế ả ế ề ả ườ
c n m t nhi u th i gian và công s c. Trong nh ng năm g n đây, trong các đ thiầ ấ ề ờ ứ ữ ầ ề
tuy n sinh đi h c, cao đng và đ thi THPT qu c gia bài toán kho ng cách đuể ạ ọ ẳ ề ố ả ề
đc xu t hi n và là n i dung khó, có tính phân lo i cao. Trong khi đó, nó chượ ấ ệ ộ ạ ỉ
chi m t 5% - ế ừ
10% t ng s đi m c a c bài thi. Vì v y, nhi u giáo viên còn có tâm lý xem nh ,ổ ố ể ủ ả ậ ề ẹ
ng i khi d y bài toán này.ạ ạ
Th hai: Đi v i h c sinh, đ có th làm t t đc các bài toán v kho ngứ ố ớ ọ ể ể ố ượ ề ả
cách đòi h i các em ph i n m ch c đc các ki n th c trong hình h c ph ngỏ ả ắ ắ ượ ế ứ ọ ẳ
nh ch ng minh hai tam giác b ng nhau, đnh lý Pi-ta-go, các h th c l ngư ứ ằ ị ệ ứ ượ
trong tam giác vuông, đnh lý cosin... cũng nh kh năng t duy tr u t ng, quanị ư ả ư ừ ượ
sát hình bi u di n, t ng h p, phân tích các đnh nghĩa, đnh lí... trong hình h cể ễ ổ ợ ị ị ọ
không gian. Trong khi đó, tr ng tôi l i n m trên vùng kinh t thu n nông, h uườ ạ ằ ế ầ ầ
h t gia đình các em đu có hoàn c nh khó khăn nên s quan tâm c a gia đình điế ề ả ự ủ ố
P
K
H
M
N
I
v i vi c h c t p c a các em còn nhi u h n ch , ch t l ng đu vào còn th p.ớ ệ ọ ậ ủ ề ạ ế ấ ượ ầ ấ
Chính vì v y, đi v i h u h t h c sinh, th m chí đi v i m t s h c sinh kháậ ố ớ ầ ế ọ ậ ố ớ ộ ố ọ
gi i còn có tâm lý chán n nỏ ả khi h c v bài toán kho ng cách.ọ ề ả
Th ba: Bài “Kho ng cách” trong sách giáo khoa l p 11 ch ng trình c b nứ ả ớ ươ ơ ả
đc phân ph i trong ba ti t, trong đó hai ti t lí thuy t và m t ti t bài t p. V iượ ố ế ế ế ộ ế ậ ớ
m t th i l ng ít nh v y, giáo viên khó có th v a gi ng d y lí thuy t v aộ ờ ượ ư ậ ể ừ ả ạ ế ừ
giúp h c sinh v n d ng lí thuy t vào gi i bài t p. Các ví d cũng nh các bàiọ ậ ụ ế ả ậ ụ ư
toán đa ra trong sách giáo khoa mang tính t ng quan, gi i thi u ch a rõ ràng, chiư ổ ớ ệ ư
ti t theo t ng b c c th nên h c sinh khó ti p thu, c m th y lúng túng, có thế ừ ướ ụ ể ọ ế ả ấ ể
các em hi u cách gi i nh ng không bi t nên b t đu t đâu và áp d ng th nàoể ả ư ế ắ ầ ừ ụ ế
đ gi i các bài toán.ể ả
Qua các bài ki m tra th ng xuyên, bài ki m tra đnh kì l p 11B3 tôi th yể ườ ể ị ở ớ ấ
h c sinh th ng không làm đc bài t p ph n này. ọ ườ ượ ậ ầ Vì th đi m ki m tra th ngế ể ể ườ
th p h n so v i các ph n h c khác. C th k t qu bài ki m tra 45 phút c a l pấ ơ ớ ầ ọ ụ ể ế ả ể ủ ớ
11B3 tr c khi tôi ch a đa ra ph ng pháp nh sau: ướ ư ư ươ ư
L p 11B3: ( T ng s HS :40)ớ ổ ố
Gi iỏKháTB Y uếKém
SL % SL % SL % SL % SL %
0 0 5 12,5 14 35,0 15 37,5 6 15,0
2.3. Các bi n pháp đã s d ng đ gi i quy t v n đệ ử ụ ể ả ế ấ ề
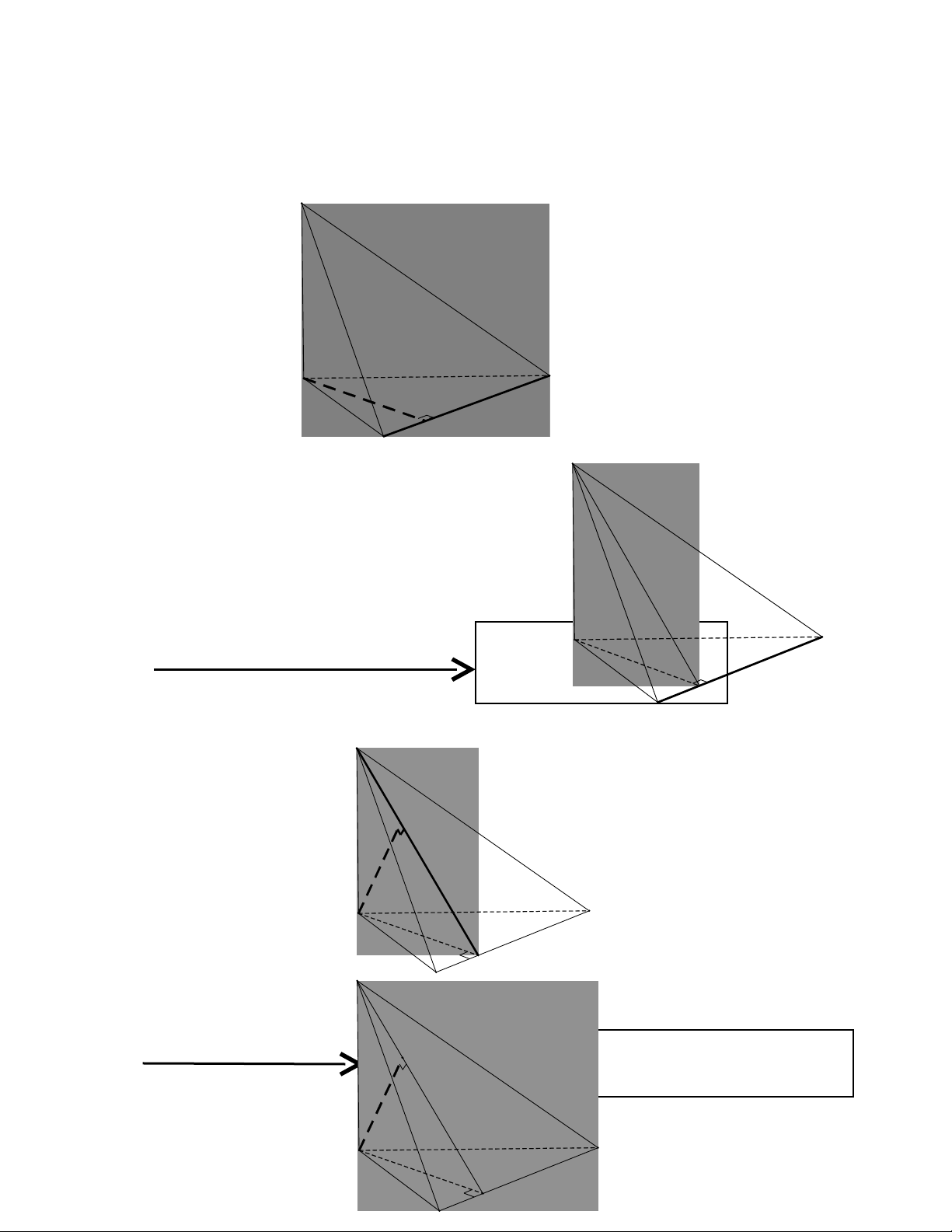
2.3.1. Bài toán c b n v tìm hình chi u c a m t đi m lên m t m t ph ngơ ả ề ế ủ ộ ể ộ ặ ẳ
Bài toán: Cho hình chóp S.ABC có
( )
SA ABC⊥
. Tìm hình chi u c a đi m A lênế ủ ể
m t ph ng (SBC). ặ ẳ T đó suy ra kho ng cách t A đn m t ph ng (SBC).ừ ả ừ ế ặ ẳ
Phân tích h ng gi i:ướ ả
Đ tìm hình chi u vuông góc c a A lên m t ph ng (SBC) ta th c hi n nh ể ế ủ ặ ẳ ự ệ ư
sau:
- B c 1ướ :
- B c 2ướ :
SA (ABC)⊥
Ch n mp(ABC) là m t ph ng ọ ặ ẳ
ch a A sao cho A là hình chi u ứ ế
c a đi m S lên m t ph ng ủ ể ặ ẳ
(ABC), v i ớ.
:
Trong mp(ABC) T A, ừk ẻ t i Iạ
Tìm giao tuy n c a (ABC) và (SBC)ế ủ
B
C
A
S
- B c 3ướ :
- B c 4ướ : Trong mp(SAI), k ẻ
AH SI⊥
t i H.ạ
- B c 5:ướ
và C/m
và C/m H là hình chi u c a A lên ế ủ
mp(SBC)
d(A,(SBC)) = AH
A
C
B
S
I
H
A
C
B
S
I
H
A
C
B
S
I
A
B
C
I
S


























