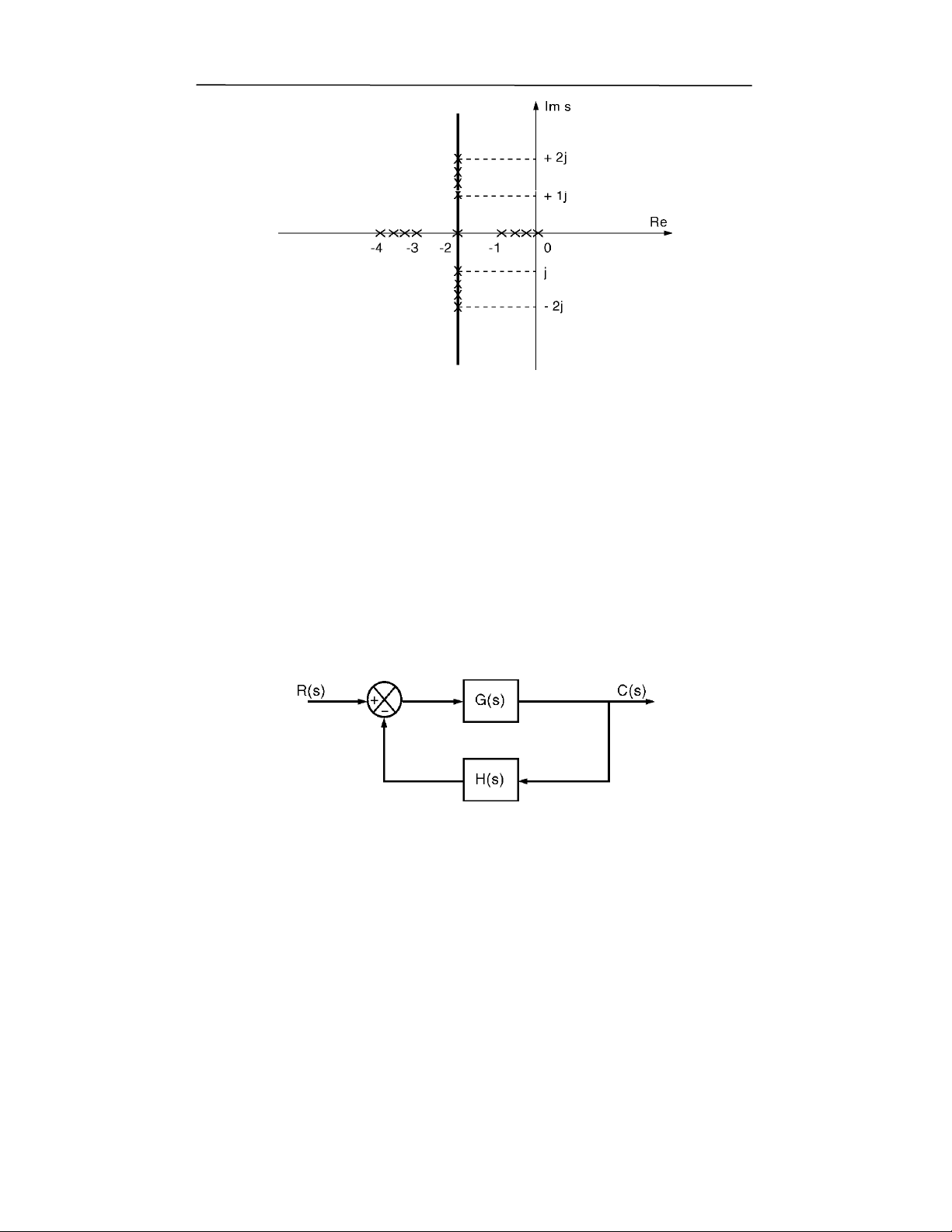
"-#+."
2
+
,3
4L>"
 P( ()  ! ( $8 9 7F ),: Lg 3< h,7F )7 )>F ( () 
,:5($8
&
/+!K,9`)97(;$(0
&
,*"0&/+,$1(,7A<
";z
∞
d, 9 F 19 , ;,( 8( ()  ! ($8 97F ) , :L g3 <h, 10
, A "7FA ) "  ! , 7 ,: + L >P  7 FA) " !  , ,:+ 
L > P "7F1( )0 1/ AO$ *P "10 )  !60; 
&'(
Z9=6'3363
.<()-6'.
92[
→
∞
0
E6>61,XAL`L=B<DI
+,35
s ,   ,0; )" #$ % & (0 6F" 0# %0; F8 L 3 E
. 7F) ,: L "K( ,? ($ 8  
P ' ; '
( ) ( )
+ =
<
g3h
=$ 0; 9 @$1 )( ( O$ ,- (> PO $*P "10 )  !60 ;d ,:7F (, + ,
98
12
97F),:L"K(,?>#@1)
/
E
C '
&_ '
( )
( )
+ =
<
g3'h
,:0)"0
&
/A,0+)60;,*"0&
K,
P ' &
_ '
( )
( )
( )
=
01
/A60;(71(($8
P
[
]'^
d
6
/A60;\:0($8
P
]'^
g3'h
⇔
P '
( )
+ =
<
⇔
P ' F-1

P ' F-3
( )
( ) ( )
=
∠ = + π
'
H $"+ */ A O$ ,- (> PO $*P " 10 )  ! 6 0;( $8  , 0; )(0 
97F),:L"K(,?(0@1)g3'hk
Z7
H0 ;   ($8  O$*P "1 0 )  ! 60; p R ( ($8 9 7F)
,:L"K(,?p60;(71(($8
P
[
]'^f0
Z7

&f[
k ( (  ( $8O$ *P"1 0)  ! 6 0;Q$ ;,
9,,7A(((71(($8
P
]'^


&
,; ";
i
∞
k
6
  ($8  O $*P "10 ) !60; , ;
";
6
\:0($8
P
]'^@\6
(0A/1,;";
∞
, 0 ( ( , !
( Q ( "5 RF 8O $, -(2 >A E
Z7%
S$* P" 10 ) !6 0; "0; Q7 )O $ ,:$1( , 71(
Z7*
=0 ," &! ,: +, :$1( ,7 1( ,$0 (> #O $*P "10 )  !
60;;$,0&)60;(71(>A\:0($8
P
]'^
R + 98 0 / A!0 ,6 0;/ 8
Z 7 +
0 ( ,1 0 RF8  ( ( "7F A) , ! (  ($8  O$* P "1 0
)  !60 ;>F  ,:$1 (, 71( Q( "5 RF 8
6
( )
+ π
α = −
'
g
, , ,
= ± ±
< '
h g3h
Z7,
 0" &! ) 7P  ( ( ,  !(  >F ,: $1( , 71(/ A" &!
( 0 ,01 "0 Q ( "5 RF8
6
3 :
 :.
N!
6 6
= =
−
−
= =
− −
∑ ∑
∑ ∑
g33h
g3
>A:

/A(((71(>A((\:0($8P
]'^h
Z 7 & !,(   9g; $( 0h($8 O $*P"1 0)  ! 60;
"-#+."
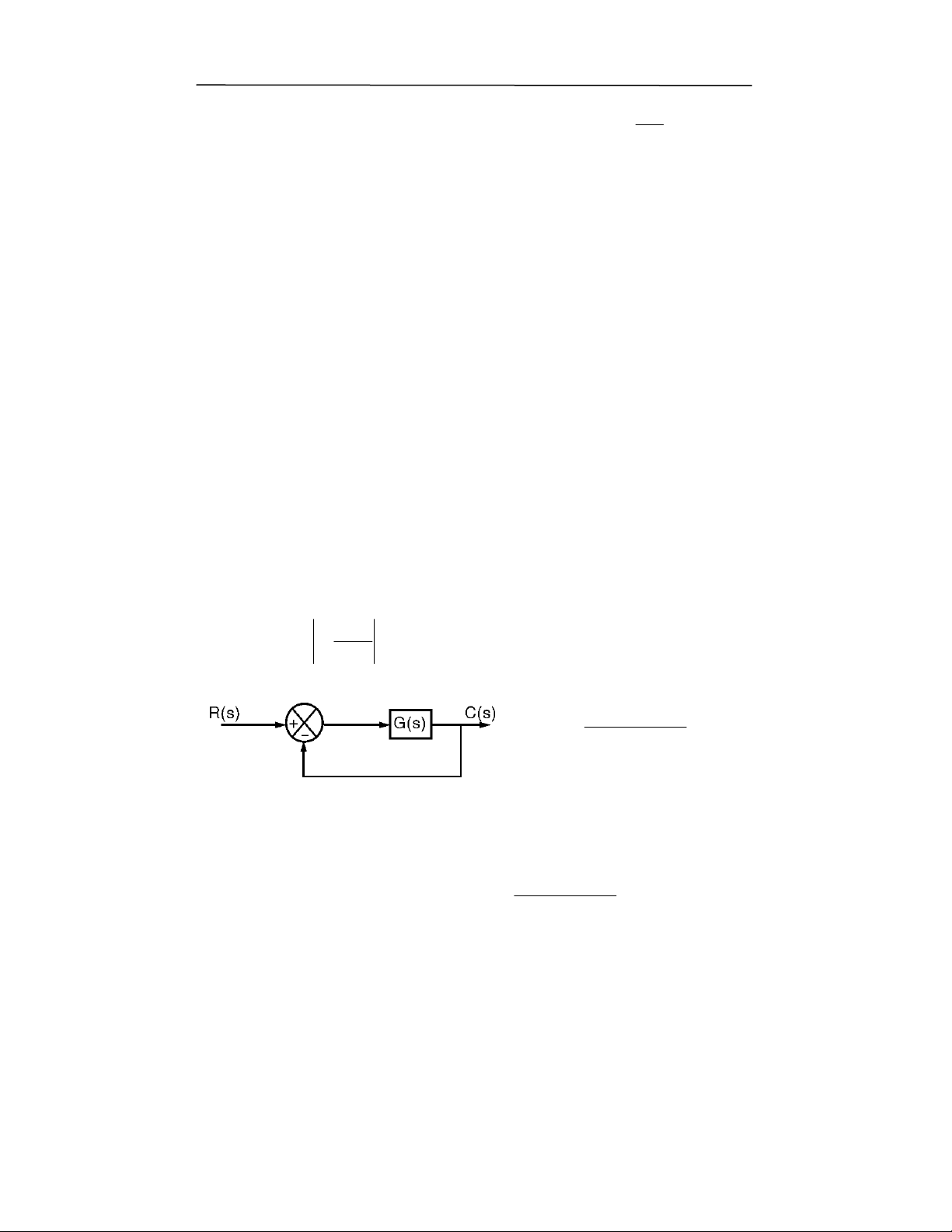
G
Y ! ,:+ ,: $1( ,71 (> A/ A ) !( $8 97F ), :L k
&
'
=
<
Z 7 /
 0"& !( $8 O$ *P"10 ) !60; >F ,:$ 1(80 (0
, &Q ( "5 R Y) !0 , ,:0 ) ( ( 6 $" +*
ZD9@$1),+$($&V0$,Z$:[,\
Z *
' d
= ω
>A0 97F) ,:L "K( ,? g3'hd (+ RY)
9#,71(>A9#806P,L!"7F1()0"&!>F,:$1(80>A),:5
&
Z7$
0 ( Q $; , 9 ,($ 8 O $*P "1 0 ) ! 6 0;, 1 ( 71( 97 (
9
~
"7F1(Q("5RF8
arg( ) arg( )
6
d d d
d
3 : 3 3
= =
≠
θ = °+ − − −
∑ ∑
N< g32h
U1)L01(($8(0+),7(,:+/A
θ
~
pN<
0
zg
∑
)0(,7A((\:0";(71(9
~
h
rg
∑
)0(,7A(((71((0A/1";(71(9
~
h
Z 7 [0 &) ( ( )  ! /A Y ) 60 ; % &,* "0& ,7A
<→z∞
Z7
 6 0;% $;( "1 @01 (, 0O$ *P " 1 0)  ! 6 0;(0 
, &Q ( "5 ,7A " #$ % R + "0
C '
&_ '
( )
( )
=
g3Eh
PCGBE6U6
 0  , 0; ),7 1"0 ) (0 6F "0# %0;  76 $

&
P ' ' ' '
( )
( )( )
=
+ +
'
+,38
 P*> PS H ($8  ,0 ;) % &p<→z∞
-6
. 7F) ,: L "K( ,? ($8  ,0; )
P '
( )
+ =
<
⇔
&
' ' '
( )( )
+ =
+ +
<
' gh
((71(kR(71(
/
N
3
=
<
d
3
= −
'
'
d
3
= −
(\:0k%0+)(0
⇒
SH)0#!(0RQ$;,9,,7A(((71(%&f[
→z∞dR($8SH6P,;";>0+($A),0
( (,  ! ( Q ( "5 RF8 k
Z 0( )7 P( ( , !(   >A ,:$ 1(, 71(
6
( ) ( )
+ π + π
α = =
− −
' '
<

⇒
'
<
π
α = =
π
α = − =
α = π =
] ^
] ^
] ^
–
Z 0 " &!) 7P ( (,  !( > A, :$1( ,7 1(
 :.
N!
6
[ ( ) ( )]
−+ − + − −
= = = −
− −
∑ ∑
< ' < 2
<
Z & !, (  9/ A)  !( $8 97 F) ,:L
&
'
=
<
(0gh ⇔ 
& ' ' ' ' ' '
( )( ) ( )
= − + + = − + +
'
' 2 E
⇒
&
' '
'
( )
= − + +
'
< E
U0"0
&
'
=
<
⇔ ' '( )
− + + =
'
< E <
⇔
' ]^
'
,
,
= −
= −
'
' 23
< GN2
Z 0"&!($8 S H> F,:$1 (8 0(0 , &Q (" 5 R Y) ! 0 ,
,:0)((6$"+*k

D9@$1),+$($&V0$,
gh ⇔ ' ' ' &
+ + + =
'
2 E <
#a
'
0 2
'
'
= 
α =
2
'
&
− × =
E <
2
<
"-#+."

'
<

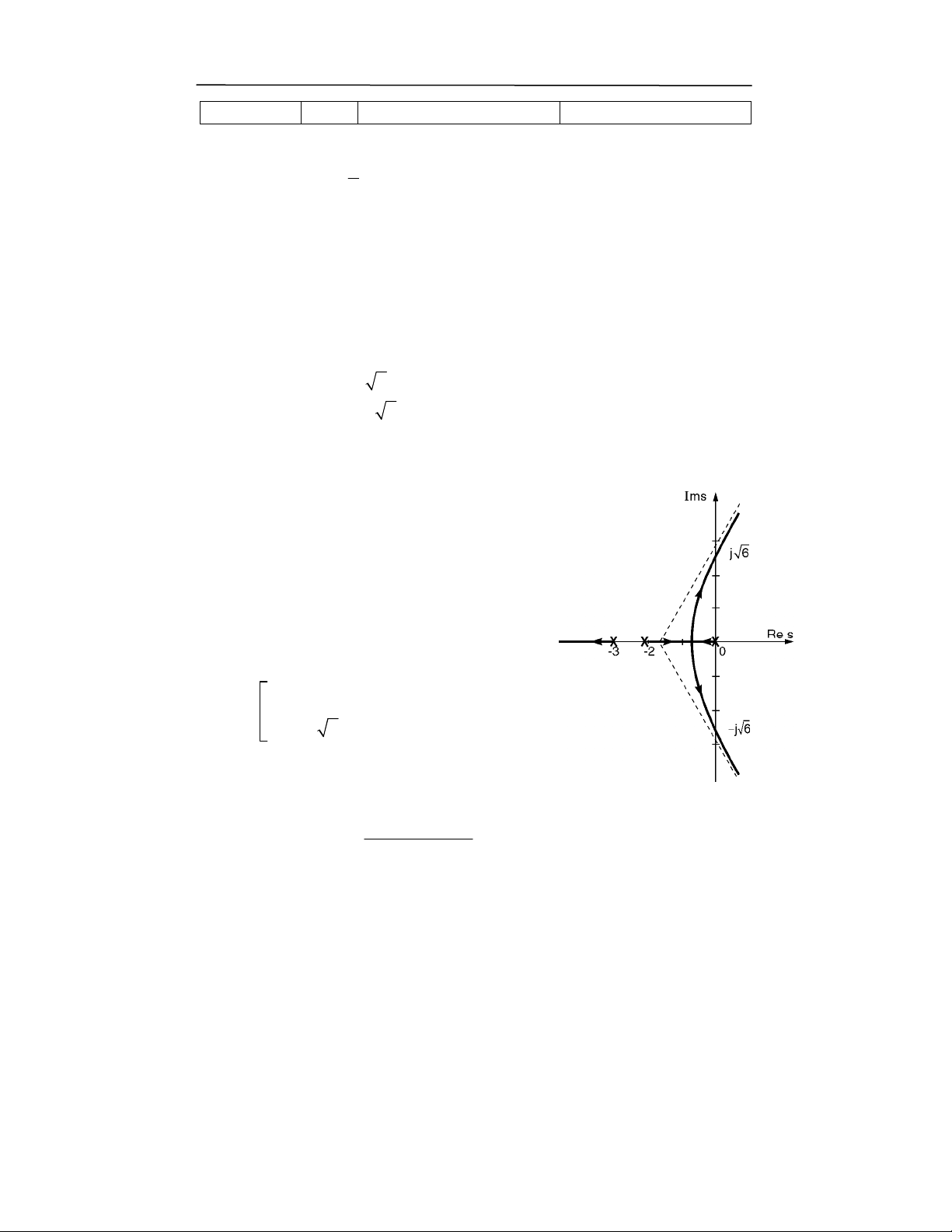
 #$ % " &  , 0; )0& "5 
&
&
− >
>
E <
2
<
⇔[n&n%[
 *   60; %$; ( "1 )F  1 /A &

p<
*),:5&

p<
>A097F),:Lg'hd)897F),:L
,"7F1()0"&!($8SH>F,:$1(80
' ' '
+ + + =
'
2 E < <
⇔
'
' d
' d
= −
=
= −
'
2
E
E

0"&!g;$(0h($8SH>A,:$1(8098(0@1)
' d
= ω

*
' d
= ω
>A097F),:Lgh,"7F1(
( ) ( ) ( )
d d d &
ω + ω + ω + =
'
2 E <
⇔d d &
− ω − ω + ω + =
'
2 E <
⇔d d
&
− ω + ω =
− ω + =
'
E <
2 <
&
ω =
=
<
<
&
ω = ±
=
E
<
PCGBE6V6
0 , 0;)0 #, ;9+! "F  > 5d ,: 0) "0  A!,:$ *# 
F8/Ak
&
P ' ' ' '
( )
( )
=+ +
'
N '<
 P*> PS H ($8  ,0 ;) % &p<→z∞
-6
. 7F) ,: L "K(, :7 )($8   , 0; )
P '
( )
+ =
<
⇔
+,39
+,39