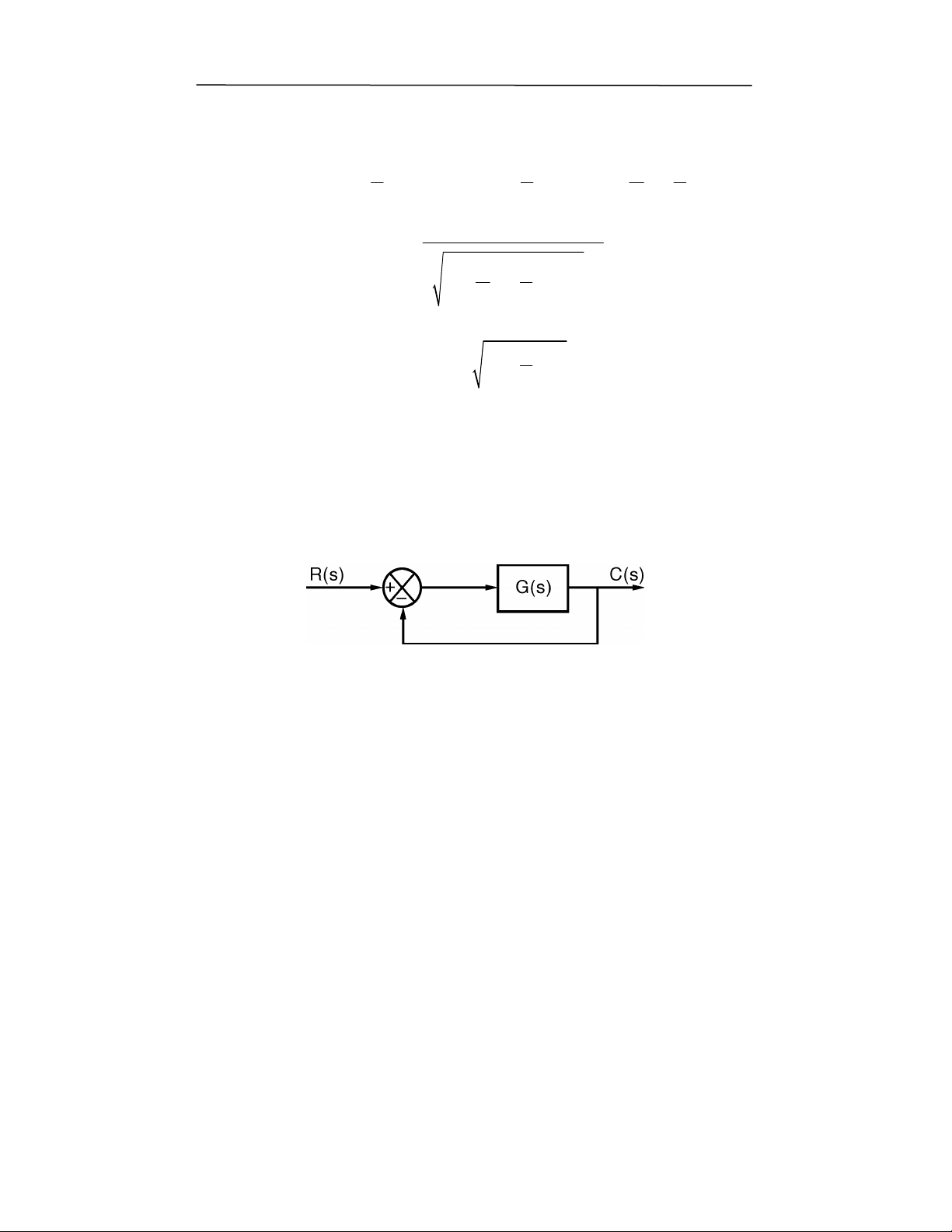
/
23
(0 "( ) ( )
−
−π −π
ϕ ω = − ω = −π
⇒ "
( )
−−π
π
ω =
⇒"
( )
−π
π
ω =
⇒
"
−π
π
ω =
U0"0
( )
−π
ω <
⇔
&
"
"
<
π
+
'
'
⇔
&
π
< +
'
E6E6E88=%G
0 , 0; ),71 "0 )( 0 6F" 0#% 0; 7 L 3 <
0R ;," K(, ?,# 60; ($8 F8 g6hdRA ,0 " K,: /A
Q , ,? 0& "5 ($8 , 0; )% ?
%
g6h
+,3.-
A0 =
; -) P
-
]'^ 2 8 P]'^
.=14 .=3
P
>
Φ >
<
<
⇒
28
PCGBE65V6
0 ,0 ;) F8(0 R &$ " 0# T 0@ 7 L > P 0 8
%?(00&"5%0+)b
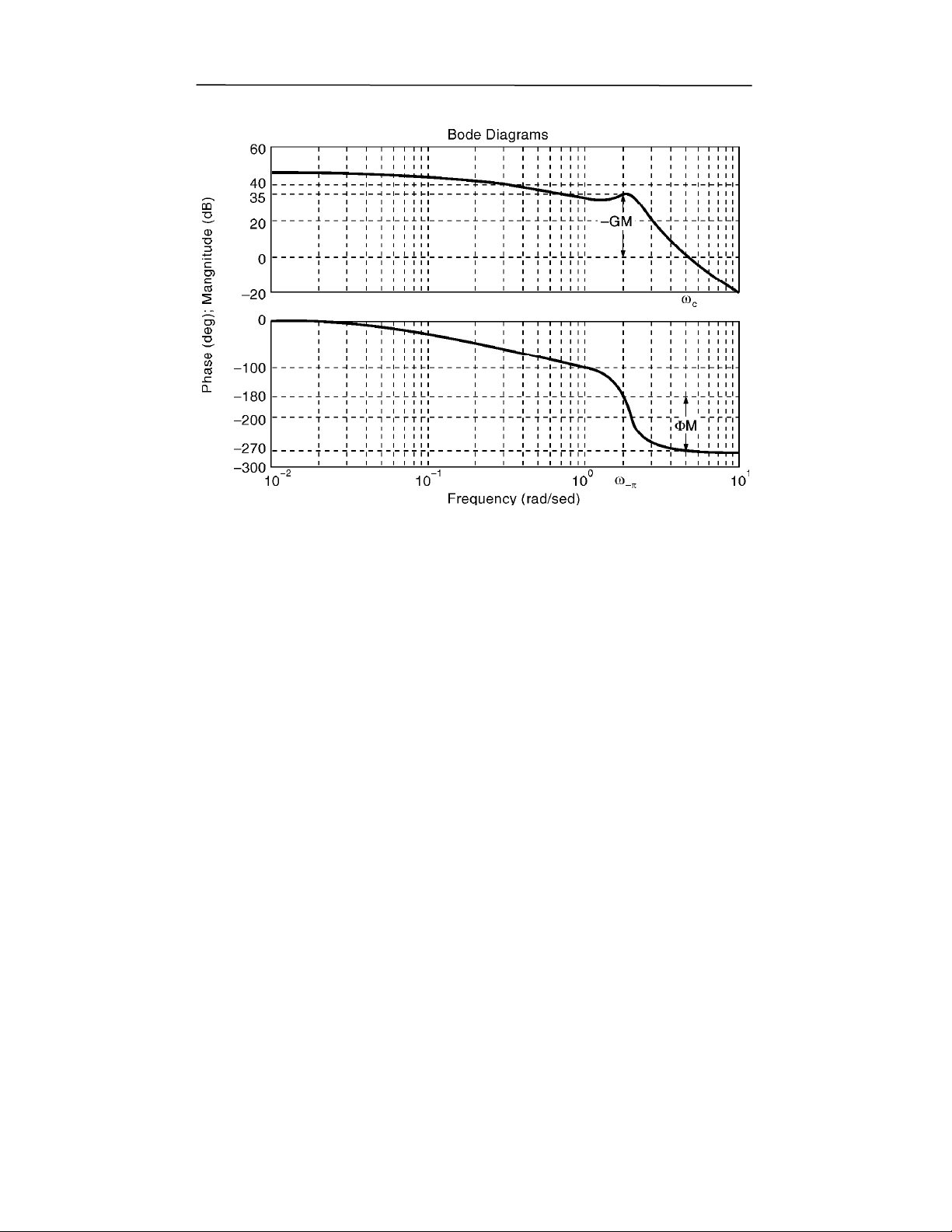
"-#+."
22
+,3..
-6
:+R&$"0#T0@,Q("5"7F1(k
,
ω =
2
g. e'hd
−π
ω =
'
g. e'h
#
( )
−π
ω =
2
⇒
P #
= −
2
( )
ϕ ω = − °
'G<
⇒
( )
Φ = ° + − ° = − °
N< 'G< <
U0=t<>AΦ= t < + ,0; )% ?% 0+) 0& " 5
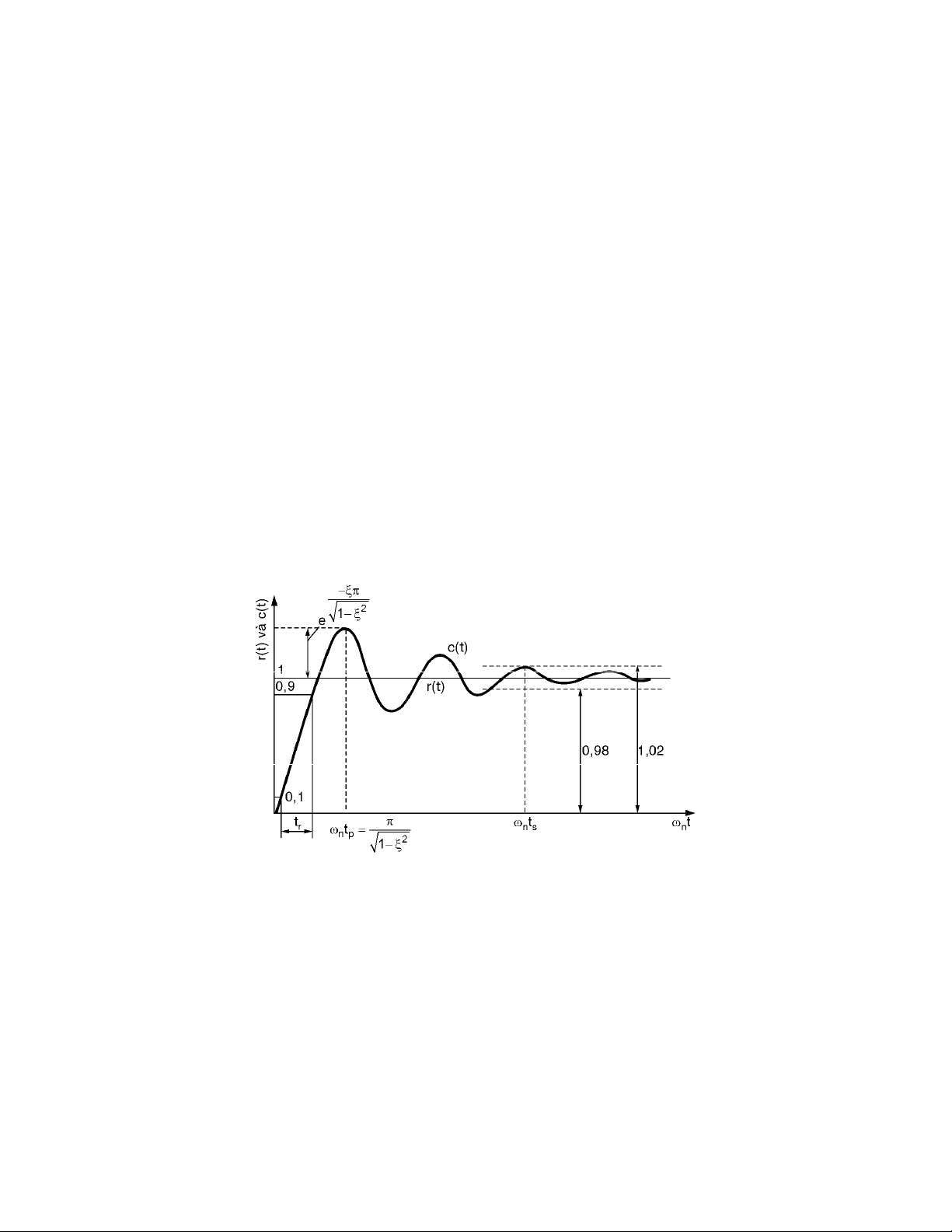
2E
)!$
"5 / A" #$ % ( # "0 ;> F !0 , d 60 )( 7
9 8 /A "$ 8" & , 0;) "7 F1( 678 @ $1) , :0) ,7 1( ,; #$ *+$ ( #$
"0 A 08 , 0; )9 8 , 08 !P "7 F1( ($ A) !0 , /$ ( ( ( , +$ ($ &
( ;, /7F1 )% ( $ 7 " 0 ( ? Q (d " 0 0 &" 5d " 9 7 ) O$
"0 d "0 1*d % 8 f) ( 0; ) j$ H $ "+ * /A !0 , 60; ,+$
( $& ,7 FA )@$A )" &" ) ( ;, /7F 1) ,0; )" #$ % &
+,4-
-6F"I %
<
lim ( ) lim ( )
? '
'H '
→∞ →
= = g2h

##$
2G
]^f.]^b]^
H 60; / A $6 0;) 7P , ? $>A 0> A, ? $ 0 #,;9 =$1 (
"?( !$0; ,? $ : O $>0A )0 #,; 9/$0+ / $0+ R! "7F1( , ?
$ >A0 !0 )! $0; #$ "0 (0 )i 6 60 ;Q (/ 9 RY )% 0+ )
.6&%]>U^
<<
m a x
%
?
?
N"
−
= × g2'h
26A
•FA)/+"^/A,FA)"97):"1,),:5(71(
"1g
3
f
3-
h
• FA ) O$ "0
'
f
'
Q("5RF8,FA"&!"97):
,7A6$"0,:F8"%0+)>7F1,:%08!#)F1660;∆O$
) , :5Q ( / 9 Y) ∆(0,&/A±'vd±2v
36&=>:>'
F8 B 08 ) ( ( ,7A ,: $1( 80 "; ) ! (71 ( )#
;,g) ! , 71( 0K (97( h"7F1( )01 / A"0 @7P ,: 7P0&"5($8
* $% 08 )( ( )- ;, ; */ Aλ
0
d;$λ
0
(A)/F,L
O$ ,: LO $"0 (A ) > #Q (/ 9 97 )O$ "0 ($8
R ( k
3
3
( )
( )
⋅ ⋅
= =
+λ
−λ
= λ = λ
∑ ∑
g2h
,:0)"0Vg9
zλ
0
h≤<
46A0 7 0
: 0) ,71 (,; !0 , , 0; ) "7F1 (, ; ,% ;9 8,0 8
* +$(# $F 8(8 (; "0 Q( / 9 > AO$ " 0 S$ ,:L O$ "0 (0
, &"7F 1(" ) ,0+ )O$ ) ,:5 ,?( 9+ ($8 6/ ( )7P
) ,:5 "K, >A ) ,:5 ,7( ,FA "0 "7F1( ($8 "1 /7F1) (# "#$
(^
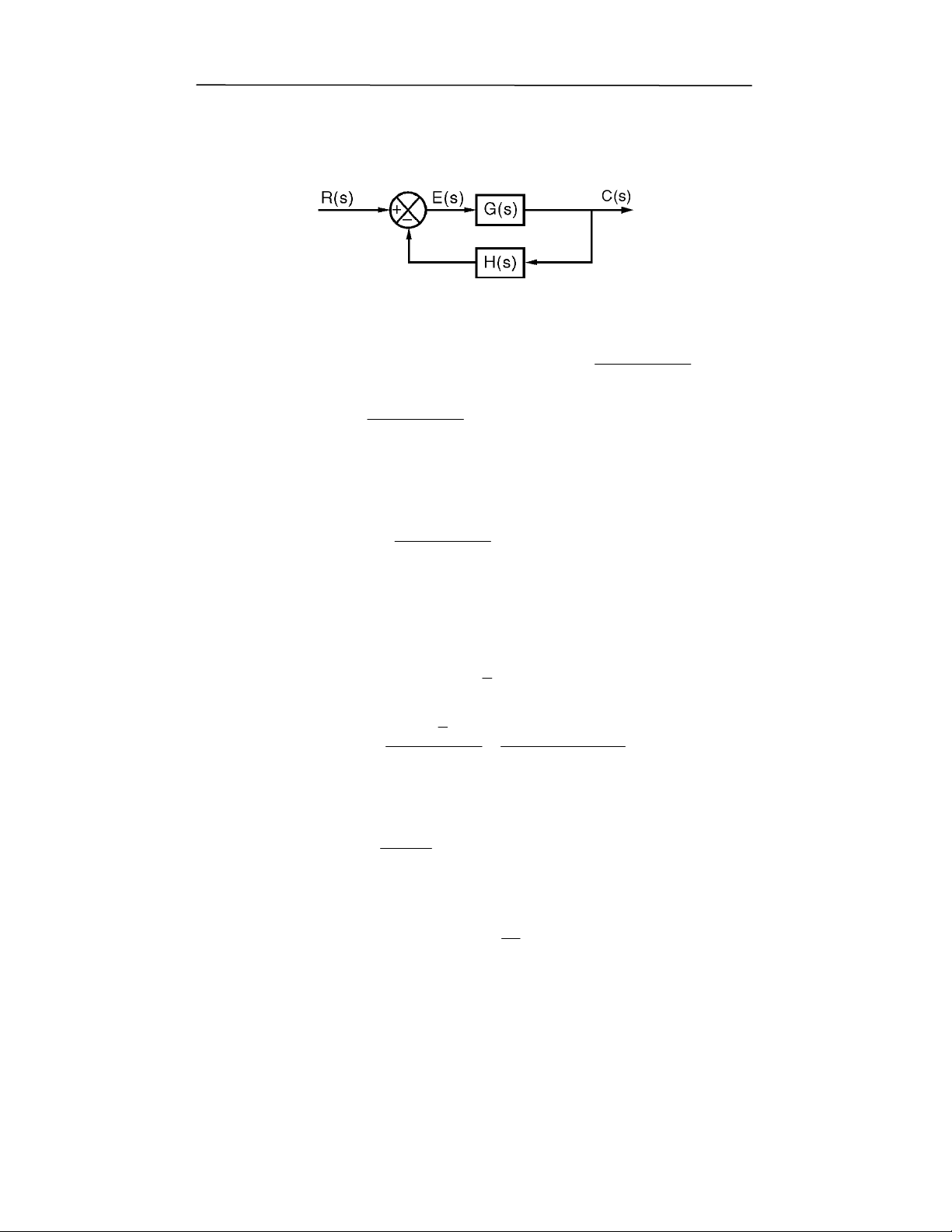
0
2N
)''/$
s , ,0; )0 # ,; 9+ !(0 6F "0# % 0; 7 L >P k
+,4.
;36
H 60; ($ 8 ,0; )/ A
P '
H ' a ' ' ; ' a ' a ' ; '
P ' ; '
( )
( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( )
= − = −
+
⇒
a '
H '
P ' ; '
( )
( )
( ) ( )
=+
H 60; Q ( / 9
? '
'H '
lim ( ) lim ( )
→+∞ →
= =
<
⇒
? '
'a '
P ' ; '
( )
lim
( ) ( )
→
=+
<
g23h
H 6 0;Q ( / 9% 0+) 7P ) 9 $1,$ 0 (>A 0( ;$,:$ (>A , 0+)
60 ;($ 8 ,0; )! A( 0A9 $1 ,$0 ( >A0 ,? $> A0
-6A7% '
.
( ) ( )
=⇒ a '
'
( )
=
? '
'
''
P ' ; ' P ' ; '
lim
( ) ( ) lim ( ) ( )
→→
⋅
= =
+ +
<<
K,
3'
& P ' ; '
lim ( ) ( )
→
=
<
k 60; >5 ,:?
⇒
?
3
&
=+
g22h
.6A7%= '
.
( ) ( )
=
⇒
a '
'
( ) =
'


![Giáo trình lý thuyết kỹ thuật điều khiển tự động 20 [Năm xuất bản]](https://cdn.tailieu.vn/images/document/thumbnail/2011/20110119/cindy03/135x160/lythuyetdieukhientudong_20__17.jpg)


![Giáo trình lý thuyết kỹ thuật điều khiển tự động 17: [Mô tả/Định tính - ví dụ: Kinh nghiệm, Mới nhất...]](https://cdn.tailieu.vn/images/document/thumbnail/2011/20110119/cindy03/135x160/lythuyetdieukhientudong_17__5288.jpg)
![Giáo trình lý thuyết kỹ thuật điều khiển tự động 16: [Mô tả/Định tính thêm nếu cần]](https://cdn.tailieu.vn/images/document/thumbnail/2011/20110119/cindy03/135x160/lythuyetdieukhientudong_16__6022.jpg)
![Giáo trình lý thuyết kỹ thuật điều khiển tự động 15: [Mô tả/Định tính - Ví dụ: Tổng quan, Chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2011/20110119/cindy03/135x160/lythuyetdieukhientudong_15__542.jpg)
![Giáo trình lý thuyết kỹ thuật điều khiển tự động 14: [Mô tả/Định tính]](https://cdn.tailieu.vn/images/document/thumbnail/2011/20110119/cindy03/135x160/lythuyetdieukhientudong_14__585.jpg)

![Giáo trình lý thuyết kỹ thuật điều khiển tự động 12: [Mô tả chi tiết/ Kinh nghiệm học tập/ Tài liệu tham khảo]](https://cdn.tailieu.vn/images/document/thumbnail/2011/20110119/cindy03/135x160/lythuyetdieukhientudong_12__6816.jpg)

![Đề cương đề tài nghiên cứu khoa học [chuẩn nhất/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251117/duong297/135x160/26111763433948.jpg)













