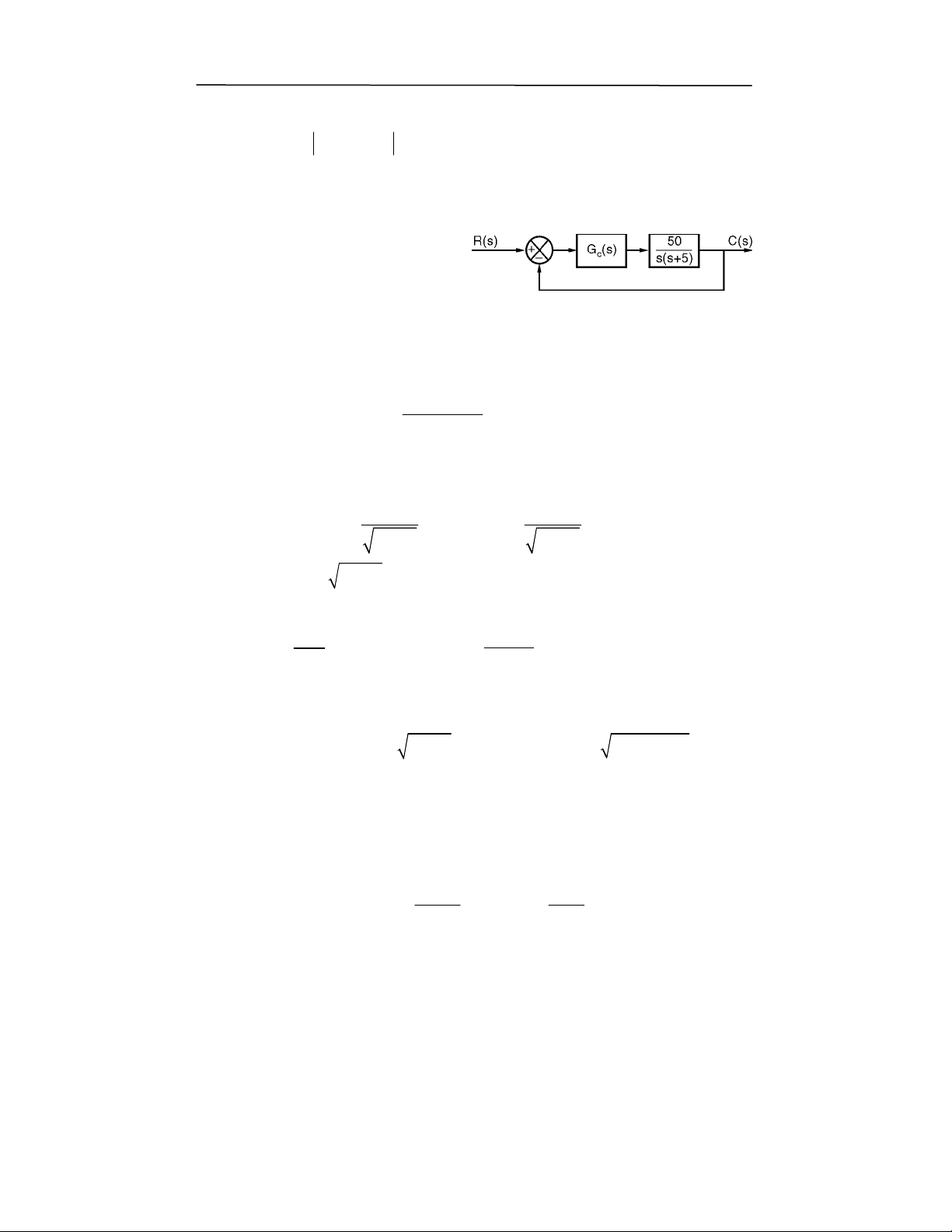
1
'
% R +" 0 U0 "0 ,9 8 ( 01 &
RY)(0+),7(k
' '
P ' P '
*
( ) ( )
=
=
PCGBT6E6
"--U'63 333
ZFCV0
0 ,0; ) " #$ % &
7 L >P P* ,;, %;
% +$ $ (^ P
g6h "& "9
7 ) O$ " 0 ($8 ,0; ) 6$
% $ (^ , 08 k. t '< vl
>
t<d26(
g,+$($&'vh
-M
L *+ $( #$, ;,% ;( 8, " 97 )O $ "0 +678 @$ 1)
% +$ $( ^ 6F !9 k
' "
P ' &
' "
( / )
( )
( / )
+ α
=+
g
α >
h
%5M
h8(3>98
0*+$(#$,;,%;d,(0k
N"
exp ,
ξπ
= − <
− ξ
'
< '
⇒
ln , ,
ξπ
− < = −
− ξ
'
< ' E
⇒,
ξ > − ξ
'
2 ⇒ ,
ξ >
'
3 N
⇒
,
ξ >
< 32
01 ,
ξ =
< G<G
,
= <
ξω
3
< 2
⇒
,
ω >
× ξ
3
< 2 ⇒
,
ω >
3
01
ω =
2
* (K 9(71 (O $*; ," 5/ Ak
' d d
*,
, ,= −ξω ± ω − ξ = − × ± −
' '
'
< G<G 2 2 < G<G
⇒' d
*,
, ,
= − ±
'
< 2 < 2
%1M
h831
U$A)(0+),7("160;
{
}
d d
*
a r g[( , , ) ] arg[( , , ) ( )]
Φ = − ° + − + − + − + − −
N< < 2 < 2 < < 2 < 2 2
, ,
a r ct a n a r ct a n
, ,
= − ° + +
− −
< 2 < 2
N<
< 2 2 2
( , )
= − ° + +
N< 2 G E
$!
⇒
*
,
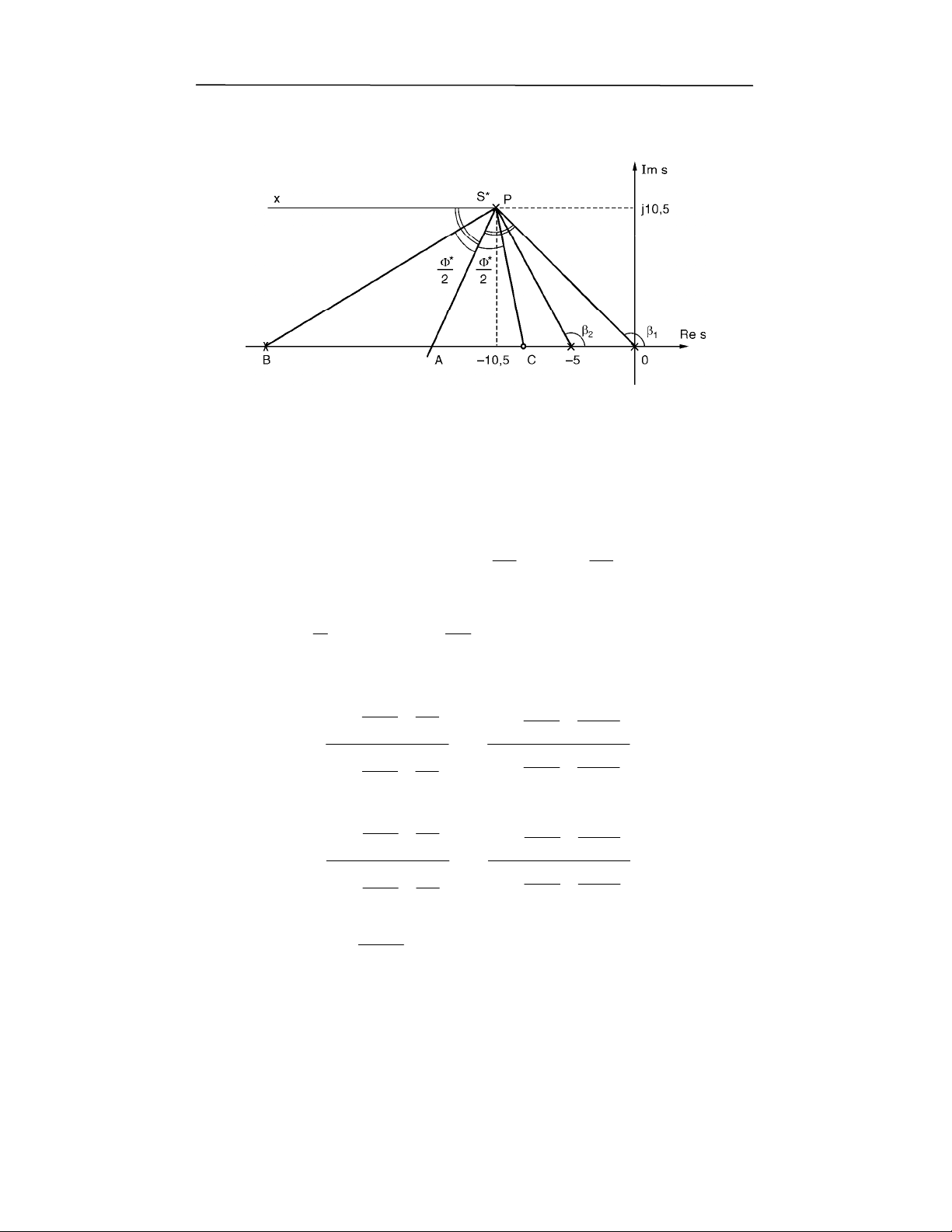
Φ = °
G' E
0U$A)(0+),7(L01(
*
( )
Φ = − ° + β + β
'
N<
( , ) ,
= − ° + ° + ° = °
N< 2 G E G' E
% >M
h 8 4 :. ($8 %+ $ $ ( ^ R Y)
97F)99"7FA)9+)(
ZP!/A9+)(($8)0(
N?
ˆ
ZP#>A60(0 !#
*
ˆ
Φ
=
'
d !
*
ˆ
Φ
=
'
&!T (? / A>5 ,:?(7 1(> A /A> 5,:?\ :0 ($8 % +$ $
(^k
N#
"
=
N
"
=
α
D 9@ $1) , 7( /7F1 ), :0 ), !) ( , 6$* : k
N?
N# N N?
*
*
ˆ,
sin sin
,
ˆ,
sin
sin
Φ° °
+
+
= = =
° °
Φ−
−
2 G' E
' ' ' '
2 'N '
2 G' E
' '
' '
N?
N N N?
*
*
ˆ,
sin sin
,
ˆ,
sin
sin
Φ° °
−
−
= = =
° °
Φ+
+
2 G' E
' ' ' '
2 N <
2 G' E
' '
' '
⇒
'
P ' &
'
( )
+
=+
N
'N
1
3
%EM
")
&
0
' '
P ' P '
*
( ) ( )
=
=
⇒
' d
'
&' ' '
, ,
.( )
=− +
+
=
+ +
< 2 < 2
N 2<
'N 2
⇒
d
&d d d
, , .
, , ( , , )( , , )
− + +
=
− + + − + − + +
< 2 < 2 N 2<
< 2 < 2 'N < 2 < 2 < 2 < 2 2
⇒
&,
, ,
×
=
× ×
< G 2<
'< 3 2 N2
⇒
&
,
=
E G
* A! ,:$ *# ( $8 % + $ $( ^ 6F !9 ( #, ;,% ;
/Ak
'
P '
'
( ) ,
+
=+
N
E G
'N
/I
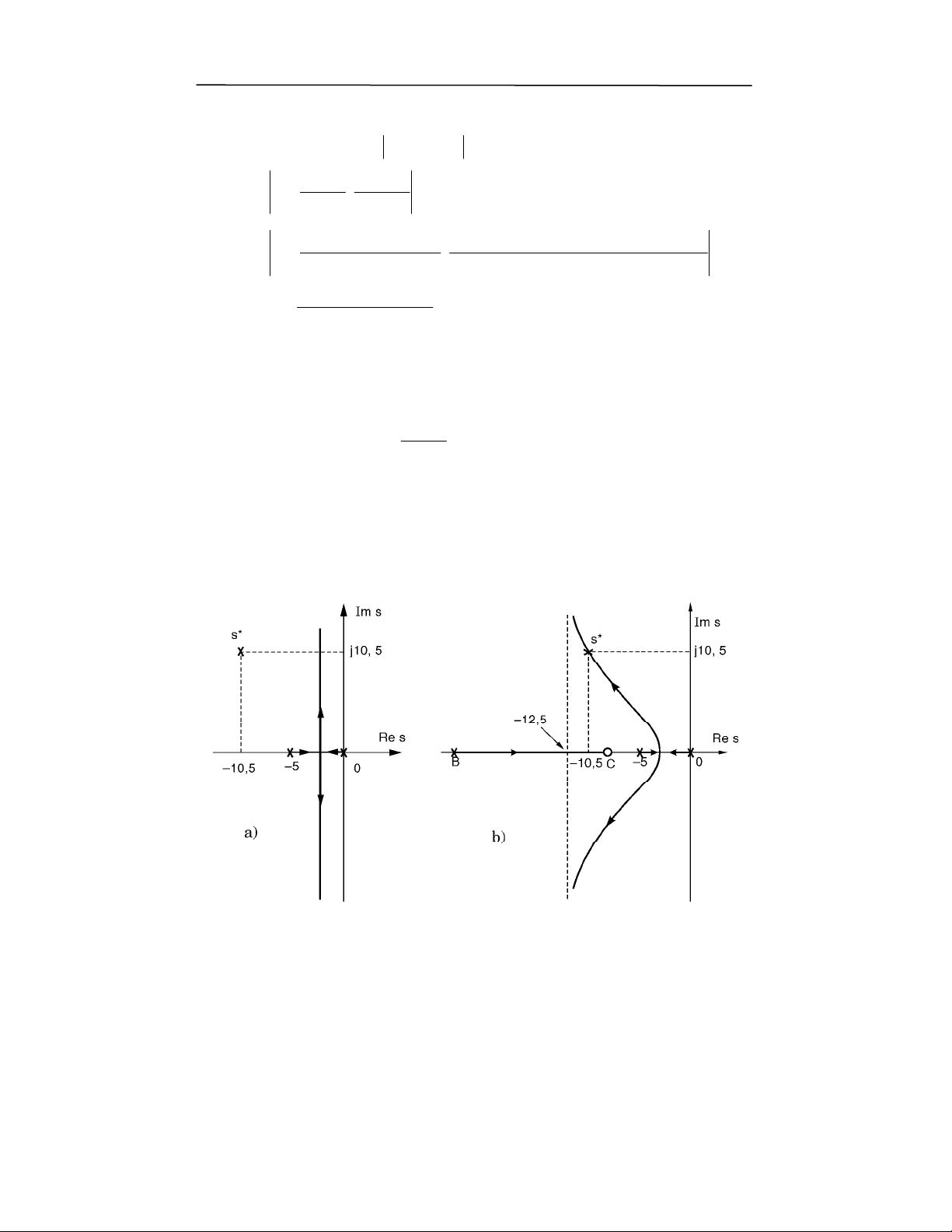
S$ *P" 10 ) !60 ; ($8 , 0; ), :7F ( % $ (^ % 0+)
O$"&!
'
*
g E Gh @0 "0 , 0; )6 P% 0+) R 0) FA" 1, " 7F1(
( ;, /7F 1) " 9 7 ) O$ "0 7 * +$ ( #$ @ $A ( 0 , * " 0& 6 0;
% $;( " 1 ($8 , 0;)
+,5-8
V92 ZFCV-U'63
^ZFCV.-Ue1^ZFCV'-U
$!
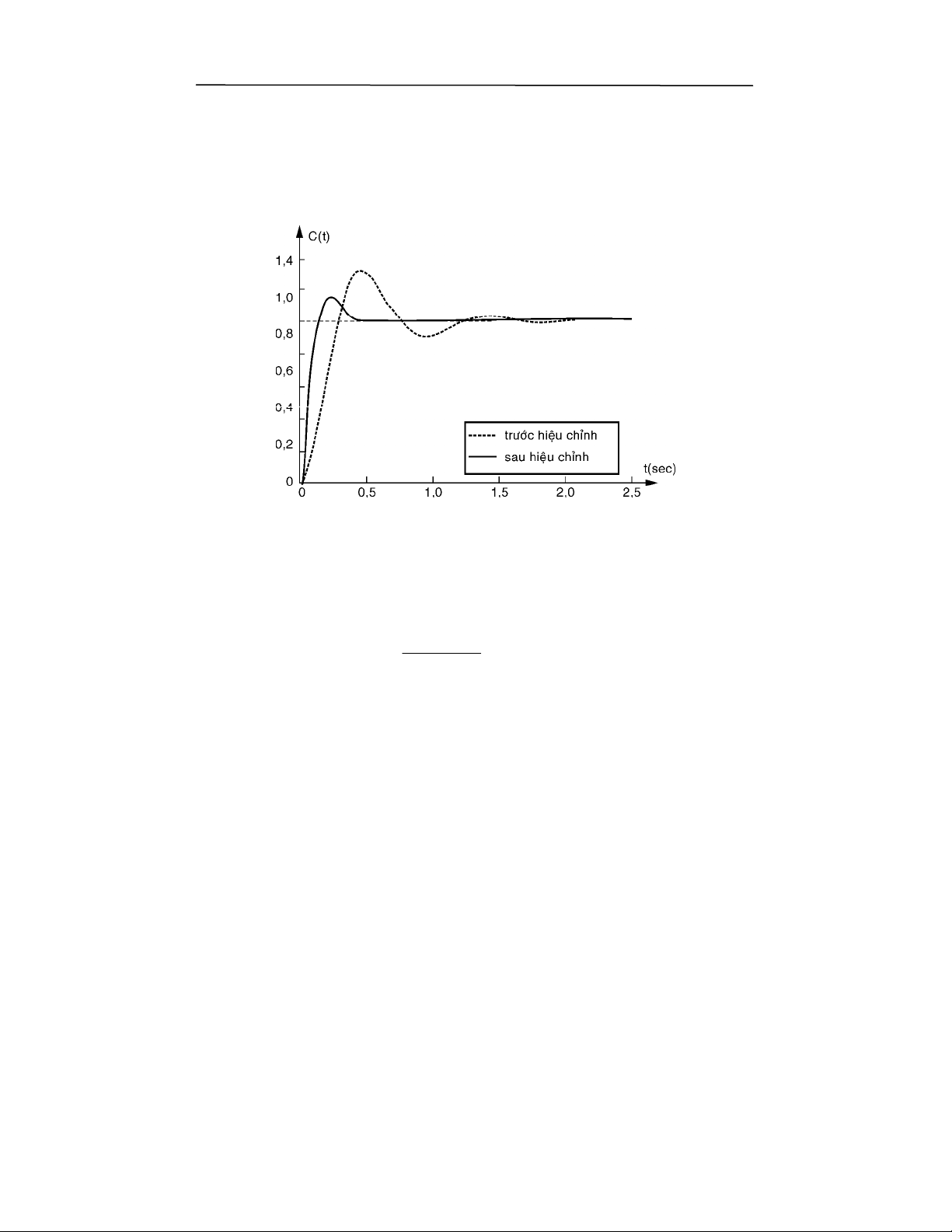
2
T Y) ( ( 678 @$1 ) % + $ $ ( ^ 6F ! 9 d O$ *P " 10
) ! 60; ( $8 ,0 ;) R 5 678 @ 1) >A O $ " &!
'
*
gEGRh
T Y) (( ( 01 6 0;% $; ("1 , ?( F1 9g 7" P, 71( F 8
R7 F(3h ,0; ) 6P (0(K 9 ( 71(O $*; , " 5 7! 0) !$ 0;d @0"0
" 97 ) O$ " 0 " 1, *+$ (# $, ; ,% ;g E N h
+,5-9
F34) ,0*
.4'-U
T6>61<O?;
A! ,:$ *# % +$ $ ( ^ ,:j 9 ( # , ;, %; (0 @1 )k
' "
P ' &
' "
( / )
( )
( / )
+ β
=+
g
β <
h
TA,0"K,:/A(01),:5&
dβ>A" "& " 97 ) ( $8
,0 ; ),0 8 !P * +$( #$ > #6 60; Q (/ 9! A a-c /A!8
7 F8) "; " 9 7 )O$ " 0 g8 7F 8 )% 0+) " ) %& h
" P R ; , @0 % +$ $ ( ^ , :j 9 (0 6 0;%$ ;( " 1 F 8
! # ,# 6 0; , ;9 /F + ( 0, ( @$1 ) /A !) 8! 6 60 ;Q ( / 9
($ 8 , 0;) & " 97 ) O$ "0 ($8 , 0; )6 $ % $ ( ^
,: j9 ) # 7% 0+) " 0&, L( K9 ( 71( O$ *;, " 5( $8 , 0; )
,: 7F (> A6 $% $ ( ^9 8 Y! : ;, ) # $ &" 1,"7 F1(
" #$ A *, 9 8 "K ,, +! (7 1( > A\ :0 ( $8% + $ $ ( ^ ,: j
960(0@1)SH,*"0&%0+)")%&+*/A)$*+
,- (( #,$ +, 0% , ; ,% ;% +$ $ ( ^,: j 9 : L,71
,;,%;@7F"+*($1,&0)$*+,-(,:+k
1
E
A:,
&Uk
?;
33-
,'Q
%5M
h8β
,7A *+ $( #$ ># 6 60; Q (/ 9
;$ *+ $( #$ ># 6 6 0;Q ( / 9( 0@ 7F @1 ) 60 ;> ,0 ;(
Y
&
*
,L,?β
RY)(0+),7(k
Y
Y
&
&
*
β =
,:0)"0
Y
&
>A
Y
&
*
/ A 60; > ,0 ;(( $8 , 0; ), :7F (> A6 $
% $ (^
%1M
:.($ 8 % +$ $ ( ^ 60 (0k
'
"
*
,
Re( )
<<
β
'
,:0)"0
'
*
,
'
/A(K9(71(O$*;,"5($8 ,0;)6$% $(^
%>M
")($8 % + $ $ (^ k
" "
.
= β
β
%EM
")&
RY)((9@$1)(0+),7(k
' '
P ' P '
*,
( ) ( )
=
=
'
,:0) "0
'
*
,
'
/ A ( K9 (71 ( O $*; , "5 ( $8 , 0; ) 6 $ % $
(^ U0 *+$ (#$ ,;, %; %0+) /A! 8 7F8) ") %& ";
" 97 ) O$ " 0 + (0 , &,? )# "$ )k
' '
*
, ,
≈
' '
S7
# k ( 0 6 0;> , 0;( ($8 , 0; ),: 7F (> A 6 $%
$ (^ / Ak
Y'
& 'P '
lim ( )
→
=
<
(
)
(
)
Y
' ' '
& 'P ' P ' P ' 'P '
*
lim ( ) ( ) lim ( ) lim ( )
→ → →
= =
< < <
(
)
Y
' '
& &
' "
& 'P '
' "
/
lim lim ( )
/
→ →
⋅
+ β
= =
+ β
< <
⇒
Y
Y
& &
&
*
β =
![Đề cương chi tiết học phần Lý thuyết điều khiển tự động [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2021/20210417/lovebychance01/135x160/5501618651902.jpg)
![Trắc nghiệm Điều khiển tự động [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250924/kimphuong1001/135x160/96131758686268.jpg)
