Ch ủ đề
4HAI Đ NG TH NG VUÔNG ƯỜ Ẳ
GÓC V I NHAUỚ
A.PH NG PHÁPƯƠ :
Đ ch ng minh đ ng th ng a vuông góc v i đ ng th ng b ta ể ứ ườ ẳ ớ ườ ẳ
có th áp d ng m t trong các cách sau:ể ụ ộ
1)Ch ng minh góc gi a a và b b ng .ứ ữ ằ
2)Ch ng minh a vuông góc v i m t ph ng ch a b.ứ ớ ặ ẳ ứ
3)Ch ng minh a song song v i c,c vuông góc v i b.ứ ớ ớ
4)S d ng đ nh lý ba đ ng vuông góc.ử ụ ị ườ
5)Đ a v m t m t ph ng ,s d ng các đ nh lý trong hình h c ư ề ộ ặ ẳ ử ụ ị ọ
ph ng. ẳ
0
90
K
M
A
B
C
D
H
Ví d 1ụ
CABRI
Cho t di n đ u ABCD,AH vuông góc ứ ệ ề
(BCD),M là trung đi m AH.ể
Ch ng minh r ng :ứ ằ
a)Các c nh đ i di n c a t di n vuông ạ ố ệ ủ ứ ệ
góc v i nhau t ng đôi.ớ ừ
b)Ba đ ng th ng MB,MC,MD vuông ườ ẳ
góc v i nhau t ng đôi.ớ ừ
K
S
AB
C
I
Ví d 2ụ
CABRI
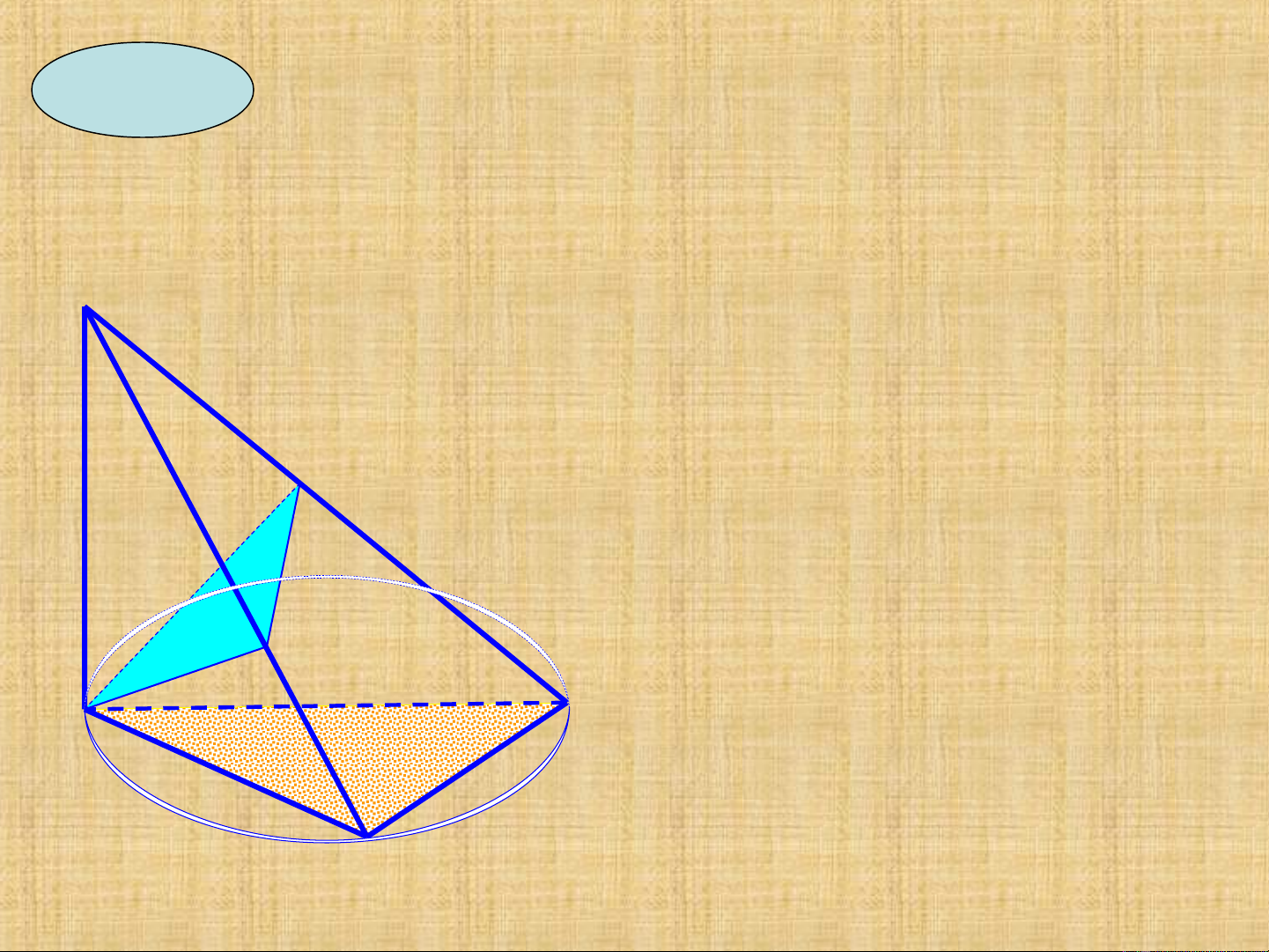
Cho hình tròn tâm O,đ ng kính AB n m ườ ằ
trong m t ph ng (P).Trên đ ng vuông ặ ẳ ườ
góc v i (P) t i A l y đi m S,trên d ng ớ ạ ấ ể ườ
tròn (O) l y đi m C,k AI vuông góc ấ ể ẻ
SC,AK vuông góc AB.Ch ng minh r ng:ứ ằ
a)Các m t t di n SABC là các tam giác ặ ứ ệ
vuông.
b) AI vuông góc IK,IK vuông góc SB.
I
S
A
B C
D
Bài 2.4.1
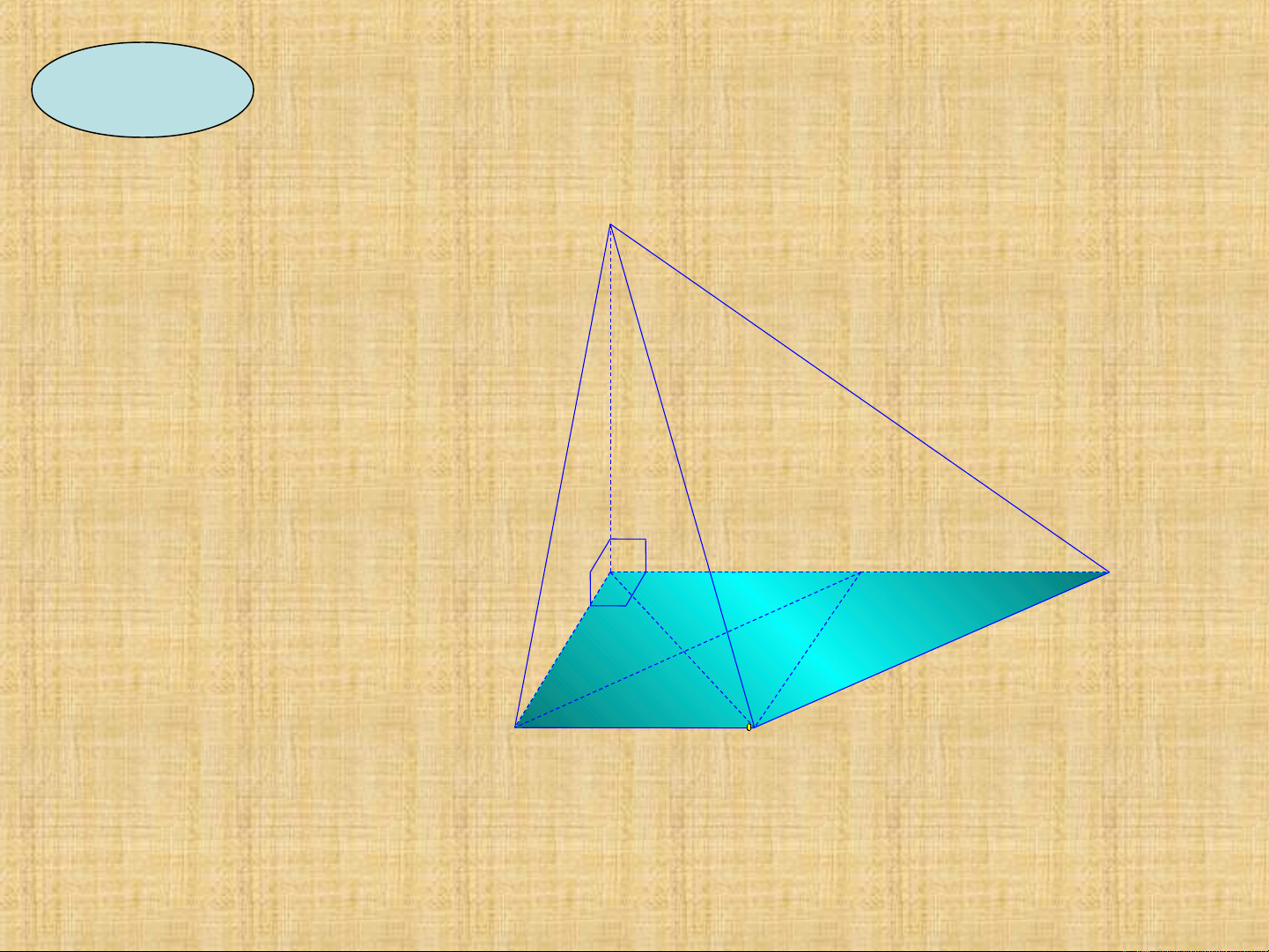
Cho hình chóp
S.ABCD có đáy là
hình thang ABCD
vuông A và ở
B,AD=2AB=2BC.
a)Ch ng minh ứ
các m t bên c a ặ ủ
hình chóp là
nh ng tam giác ữ
vuông.
b)G i I là trung ọ
đi m c a AD ể ủ
ch ng minh BI ứ
vuông góc SC và
CI vuông góc SD.
I
A
S
C
B
H
Bài 2.4.2
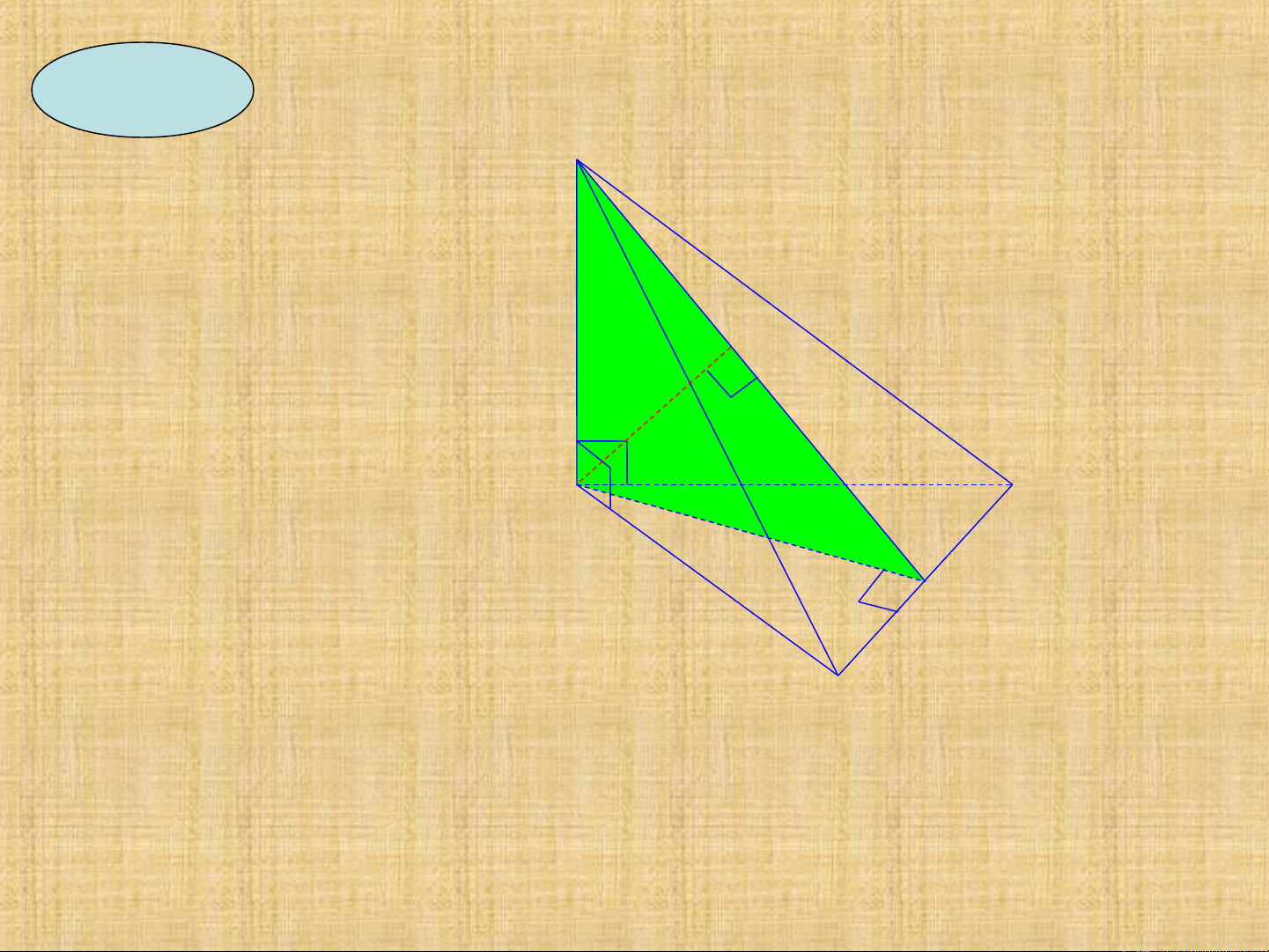
Cho hình chóp S.ABC có
SA vuông góc
(ABC),AB=AC,I là trung
đi m c a BC ể ủ
AH vuông góc SI.Ch ng ứ
minh:
a)BC vuông góc AH.
b)AH vuông góc SB.
c)SC không vuông góc
v i AI.ớ
⊥