ntsơn
Chương 2
III. Ngữnghĩa của
luận lý mệnh đề
ntsơn
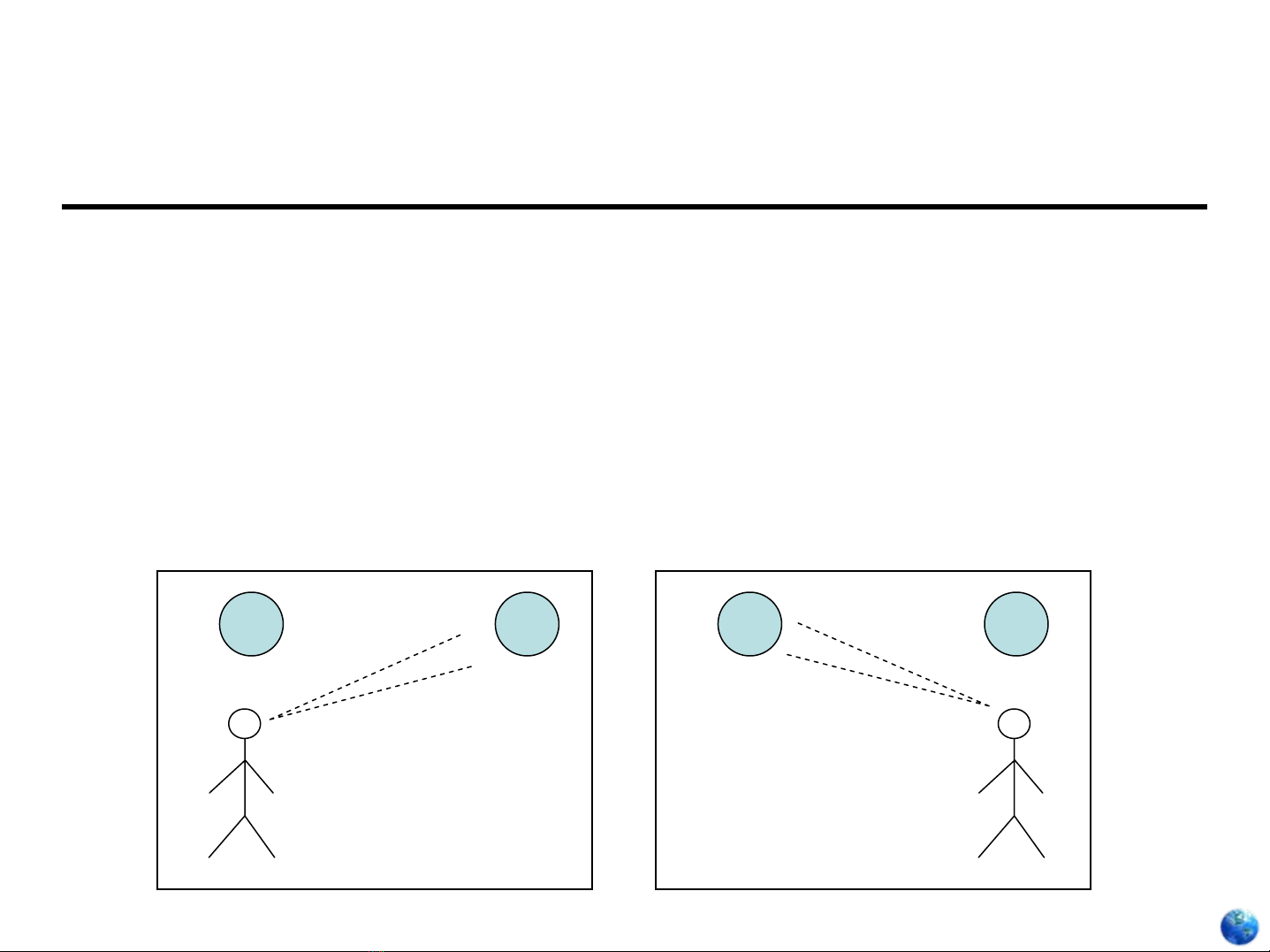
Thái độ
•Tựthân đối tượng A, B không có “ý nghĩa” gì.
Nó chỉcó ý nghĩa khi có chủthể“nhìn” nó.
•Chủthể đứng ở đối tượng A nhìn đối tượng B,
khác với khi chủthể đứng ở đối tượng B nhìn
đối tượng A.
A B A B
ntsơn
Diễn dịch
•Côngthức của LLMĐ tựthân không có giá trị
đúng sai.
•Muốn có giá trị đúng sai của của công thức phải
“nhúng” nó vào một thếgiới thực.
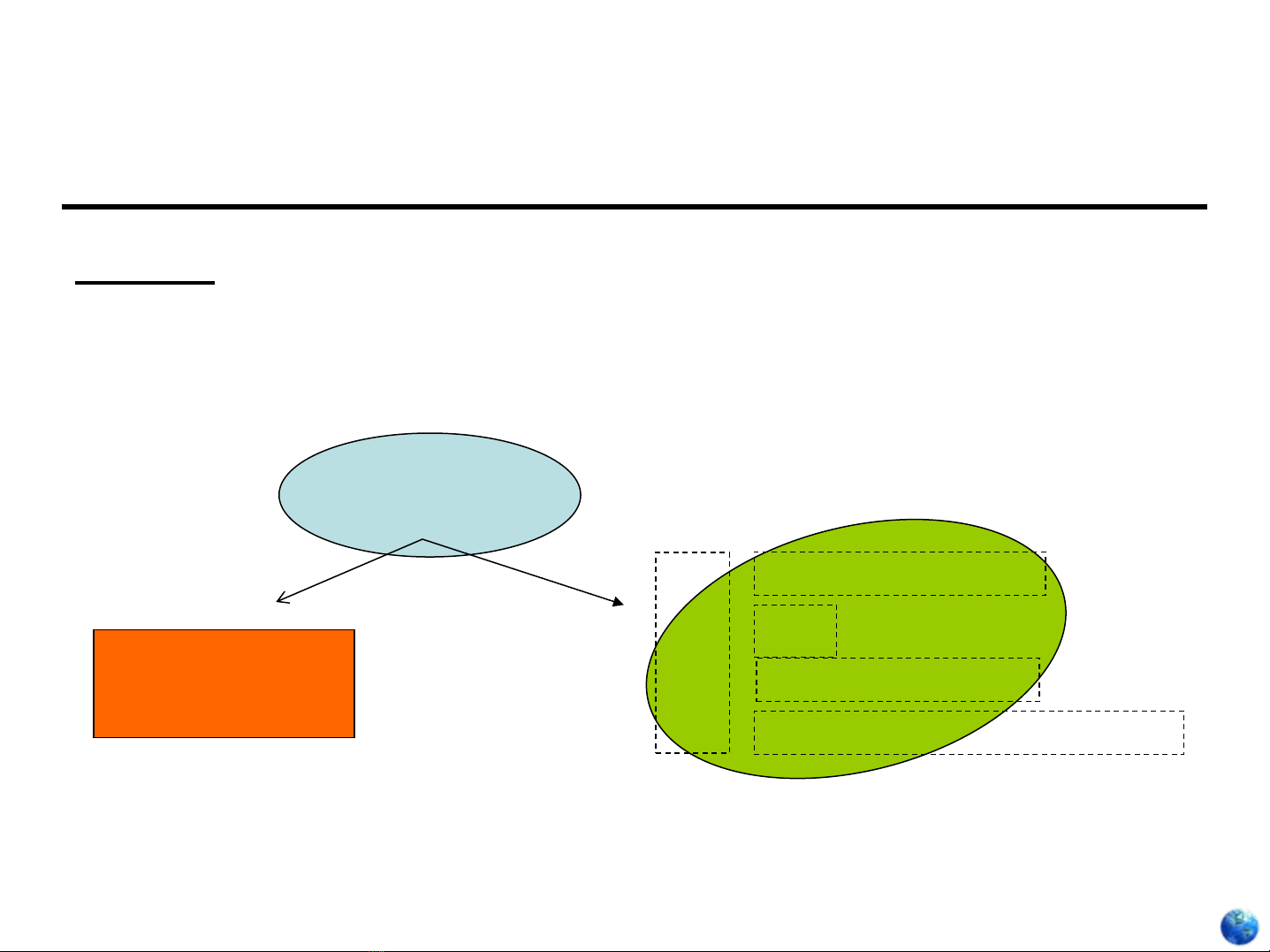
•Diễn dịch của một công thức là thếgiới thực
cùng với cách nhúng từng yếu tốcủa công thức
vào thếgiới thực đó.
• Nói cách khác diễn dịch là “gán” cho công thức
một ý nghĩa của thếgiới thực mà nó được
nhúng vào.
ntsơn
Diễn dịch
Thí dụ:
Công thức ((H ∧O) →W) chưa có giá trị đúng sai.
Thếgiới Luận lý mệnh đề
Thếgiới thực (hoá học)
Thếgiới thực (văn học sử)
(H ∧O) →W
H2+ O2→H2O
H HồDzếnh là nhà thơ
O Gái quê là 1 tập thơ
W HồDzếnh là tác giảcủa Gái quê
∧và
Nếu
→
thì
…
ntsơn
Diễn dịch
•Việc khảo sát công thức chỉ quan tâm đến giá
trị đúng sai của công thức trong từng thếgiới
thực.
•Dùsốthếgiới thực là vô hạn, nhưng
mỗi công thức chỉcó hữu hạn các CTN,
nên chỉcó hữu hạn trường hợp đánh giá đúng
sai cho mỗi công thức trong mọi thếgiới thực.