ÔN TẬP MÔN NGUYÊN LÝ THỐNG KÊ
Ậ
Phân tổ với các khoảng cách tổ bằng nhau.
max min
ii
i
XX
hn
Trong đó:
i
h
: Trị số khoảng cách tổ.
max
i
X
: Lượng biến lớn nhất của tiêu thức phân tổ.
min
i
X
: Lượng biến nhỏ nhất của tiêu thức phân tổ.
n
: Số tổ cần chia.
ác bước phân tổ thống kê:
Bước 1: Lựa chọn tiêu thức phân tổ.
Bước 2: Xác định số tổ cần phân và khoảng cách tổ.
Bước 3: Phân phối các đơn vị vào từng tổ.
Ố
ST
T
Công thức
ơn
vị
Chú thích
ố tu t đối t ời v số tu t đối t ời đi
1
§§
TG
T
§
TLH
T
1
§§
0
TG
y
Ty
§
1
i
TLH
i
y
Ty
%,
pđv
1
y
: Mức độ của hi n tượng k nghiên cứu.
0
y
: Mức độ của hi n tượng k gốc.
§§
TG
T
: Số tương đối động t ái định gốc (Tốc độ PT định gốc).
§
TLH
T
: Số tương đối động thái liên hoàn (Tốc độ PT liên hoàn).
2
KH
T
0
KH
KH
y
Ty
%,
pđv
KH
T
: Số tương đối nhi m vụ kế hoạch.
TK
T
: Số tương đối hoàn thành kế hoạch.
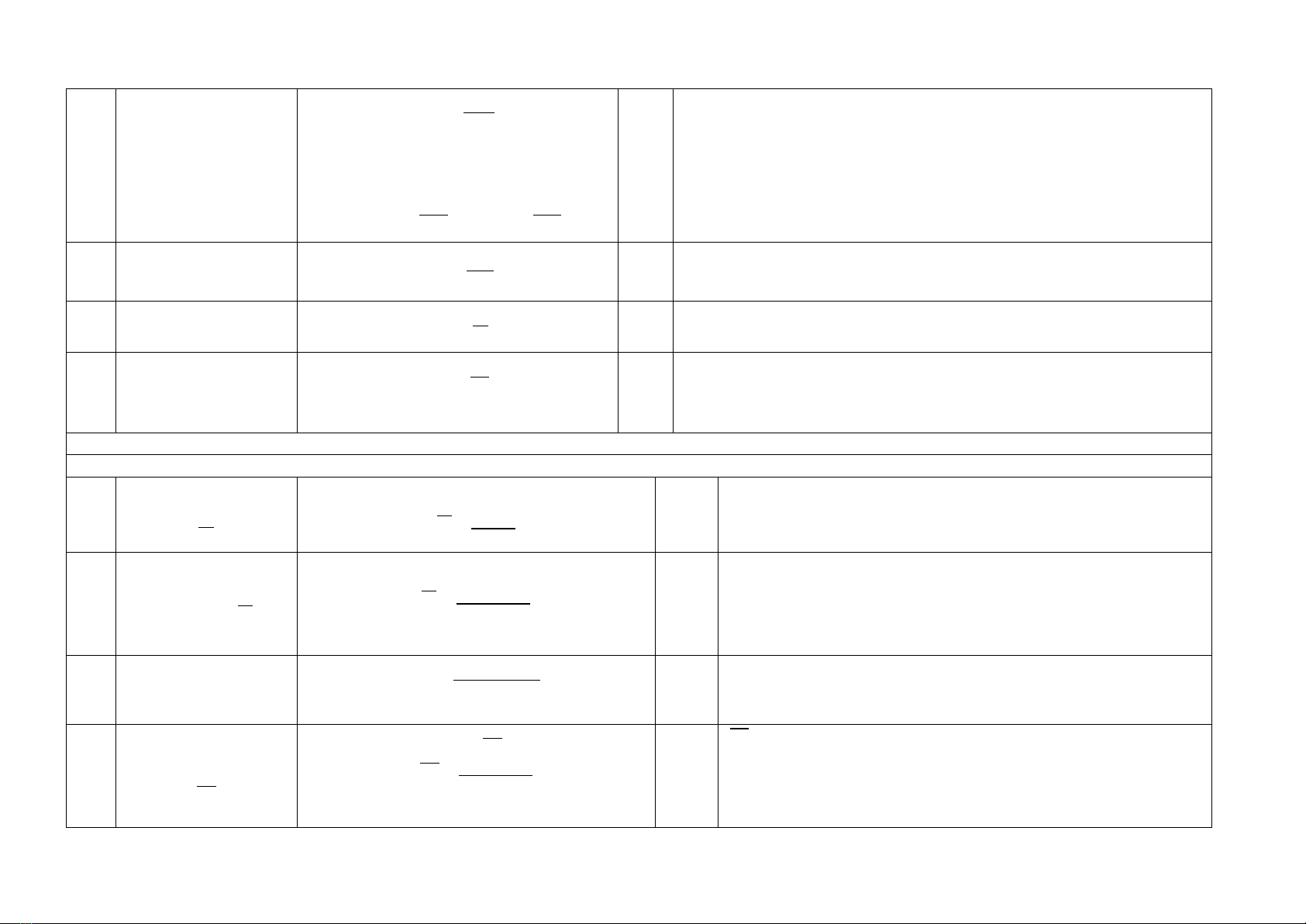
TK
T
1
TK
KH
y
Ty
Hệ quả:
DT KH TK
T T T
DT
TK
KH
T
TT

v
DT
KH
TK
T
TT
KH
y
: Mức độ của hi n tượng k kế hoạch.
0
y
: Mức độ thực tế của chỉ tiêu ở k gốc so sánh.
1
y
: Mức độ của hi n tượng k báo cáo.
3
KC
T
bq
KC
TT
y
Ty
%,
pđv
bq
y
: Mức độ của bộ phận.
TT
y
: Mức độ của tổng th .
4
CD
T
§
C
m
Tn
%,
pđv
m
: Mức độ của hi n tượng cần đán giá p ổ biến.
n
: Mức độ của hi n tượng n o đó có liên quan.
5
KG
T
1
2
KG
x
Tx
%,
pđv
1
x
: Mức độ của hi n tượng ở không gian thứ nhất cần phân tích.
2
x
: Mức độ của hi n tượng ở không gian thứ ai dùng l cơ sở so
sánh.
1
X
1
n
i
i
X
Xn
đvt
i
X
: Lượng biến (i=1, 2, …, n)
n
: Số đơn vị trong tổng th .
2
X
1
1
n
ii
i
n
i
i
Xf
X
f
đvt
i
X
: Lượng biến (i=1, 2, …, n)
i
f
: Quyền số (Tần số)
ii
Xf
: Gia quyền
8
g
X
ax min
2
m
g
XX
X
(với lượng biến có khoảng cách tổ)
đvt
axm
X
: Lượng biến lớn nhất của tổ.
min
X
: Lượng biến nhỏ nhất của tổ.
3
t
X
1
1
k
ii
i
tk
i
i
Xn
X
n
đvt
i
X
: Số bình quân tổ i.
i
n
: Quyền số hoặc số đơn vị tổ i.
K: Số lượng tổ.
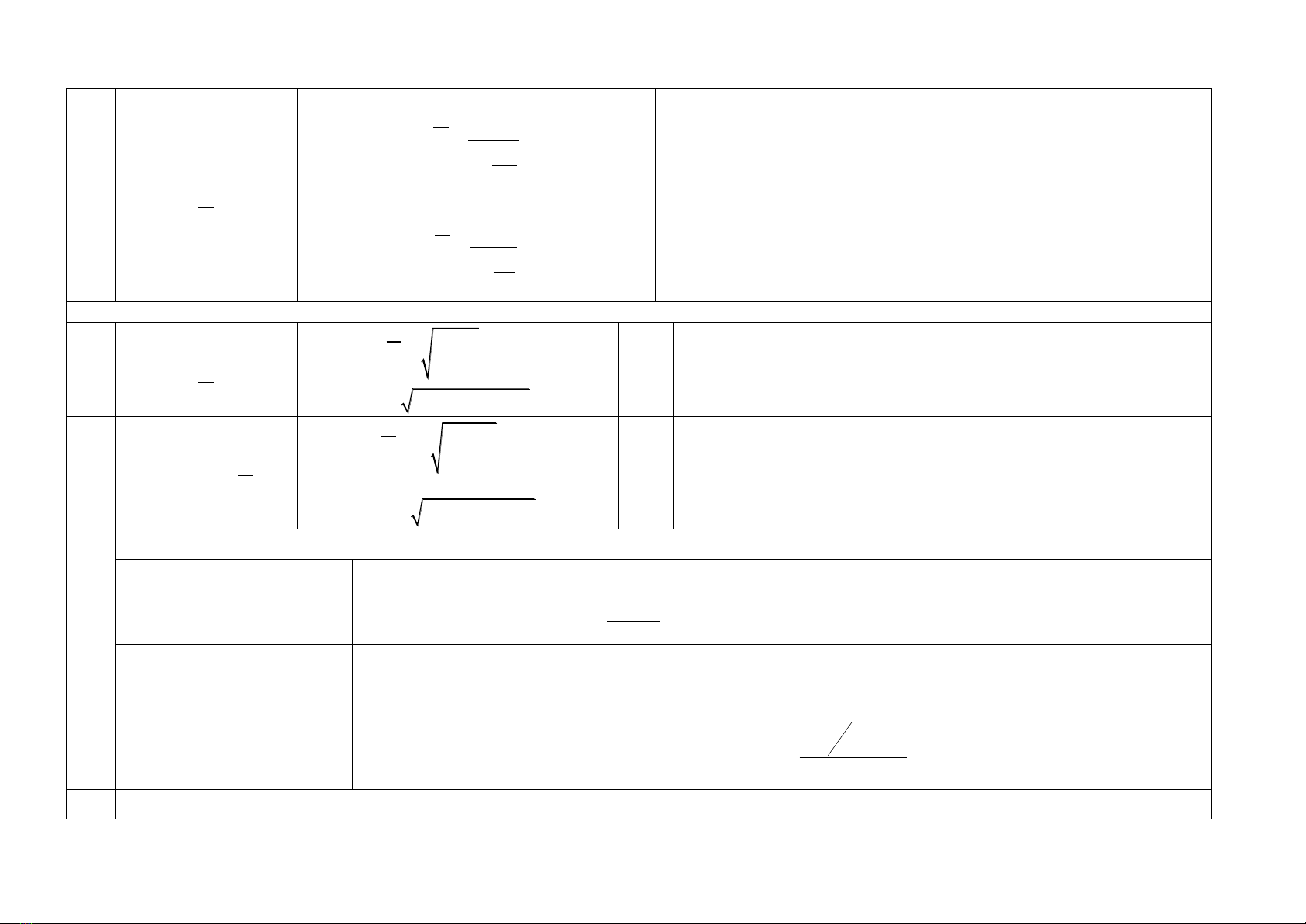
4
X
1
1
n
i
i
n
i
ii
M
XM
X
Khi:
12
... n
M M M M
thì:
1
1
n
ii
n
X
X
đvt
i i i
M X f
: Gia quyền.
(Vận dụng i c ưa biết tần số hay tần số ẩn)
1
X
1
1 2 3
. . .....
n
ni
i
nn
XX
X X X X
đvt
i
X
: Lượng biến (i=1, 2, 3,…,n)
n
: Số đơn vị ( Số lượng biến).
2
X
1
2
1
1
12
. .....
n
ii
i
n
i
i
i
n
ff
i
i
f
fffn
n
XX
X X X
đvt
i
X
: Lượng biến (i=1, 2, 3,…,n)
i
f
: Tần số tương ứng.
1
Số trung vị (MEDIAN -
e
M
)
+)Với dãy số có lượng biến
không có khoảng cách tổ:
*
2 1, eq
n k k N M x
(
q
là tổ ở giữa)
*
2, 2
qp
e
xx
n k k N M
(
,qp
là tổ ở giữa)
+)Với dãy số lượng biến có
khoảng cách tổ:
*Xác định tổ chứa
e
M
: Cộng dồn tần số (Si) đến khi nào bằng hoặc vượt quá
2
i
f
thì dừng.
*Giá trị gần đúng của số trung vị được xác định theo công thức:
min
1
2e
ee
e
iM
e M M
M
fS
M X h f
14
Số Mốt (MODE -
o
M
)
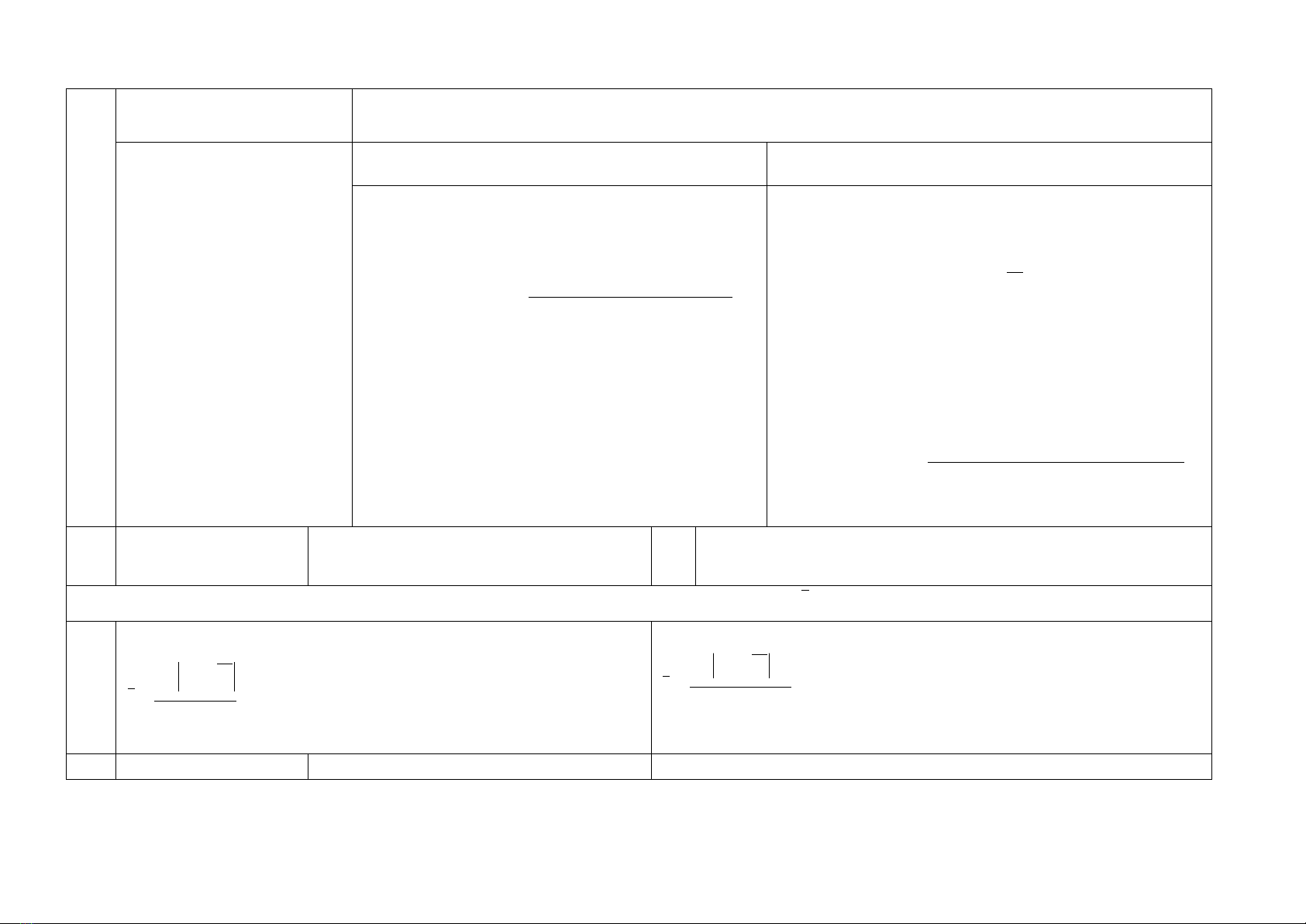
+)Với dãy số lượng biến
không có khoảng cách tổ:
axim
o
MX
(Mốt l lượng biến lớn nhất trong dã lượng biến)
+)Với dã lượng biến có
khoảng cách tổ:
TH có khoảng cách tổ đều nhau:
TH khoảng cách tổ không đều nhau.
*Tổ chứa mốt là tổ có tần số lớn nhất
max
f
Tæ
.
*Giá trị gần đúng của mốt được tính theo công thức:
min
1
11
oo
oo
o o o o
MM
o M M
M M M M
ff
M X h f f f f

*Tổ chứa Mốt là tổ có mật độ phân phối là lớn nhất
PPmax
M
Tæ
.
i
i
PP
i
f
Mh
rong đó:
i
PP
M
: Mật độ phân phối của tổ i.
i
f
: Tần số của tổ i.
i
h
: Trị số khoảng cách tổ của tổ i.
*Giá trị gần đúng của Mốt được tính:
min
1
11
M Mo
o
oo
M M M M
o o o o
PP PP
o M M
PP PP PP PP
MM
M X h
M M M M

1
Khoảng biến thiên
(
R
)
ax minm
R X X
đvt
axm
X
: Lượng biến lớn nhất.
min
X
: Lượng biến nhỏ nhất.
Ố Q (
e
)
16
+)TH không có quyền số:
1
n
i
i
XX
en
+)TH có quyền số:
1
1
.
n
ii
i
n
i
i
X X f
e
f
17
Phương sai (
2
)
+)TH không có quyền số:
+)TH có quyền số:
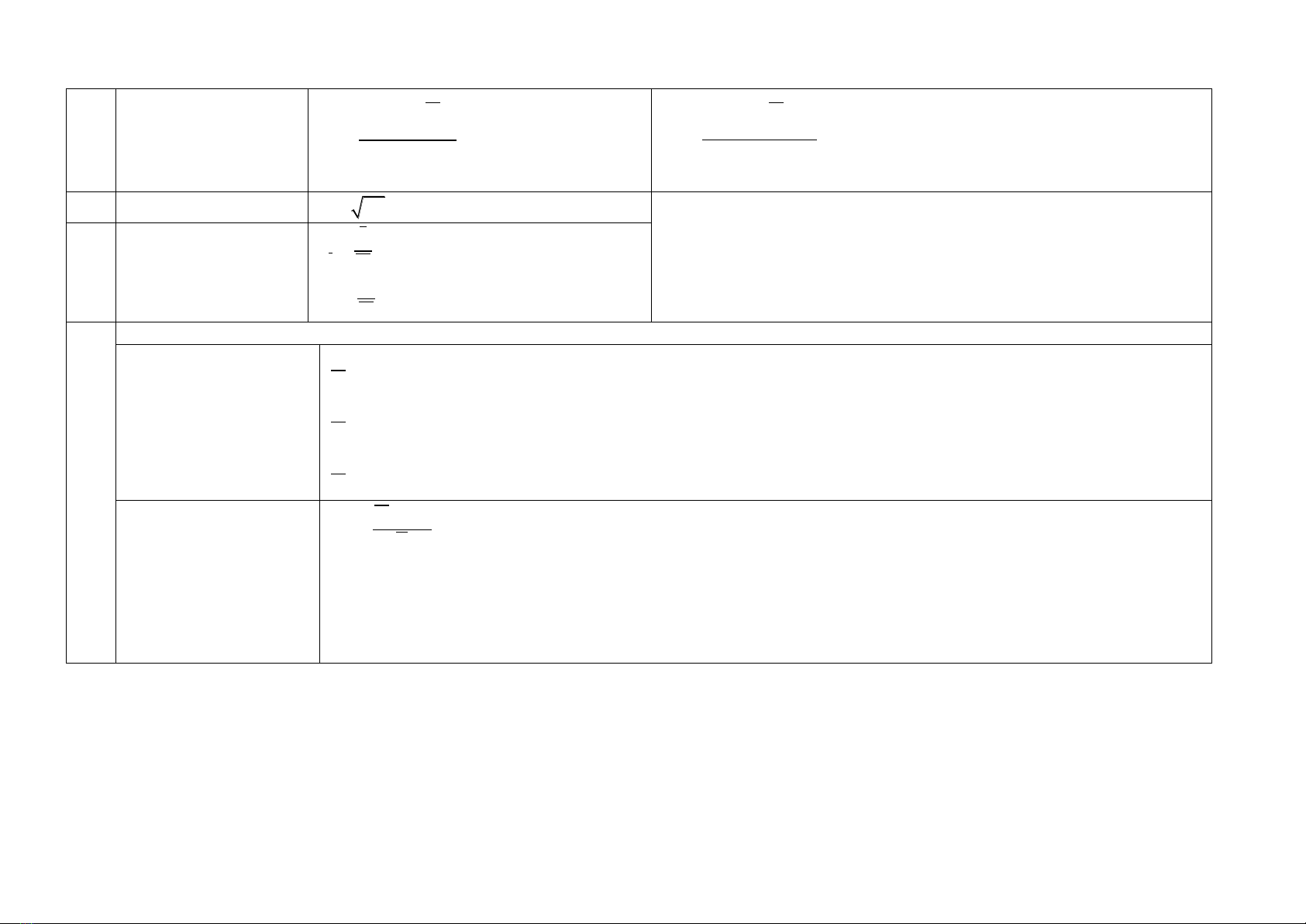
2
21
n
i
i
XX
n
2
21
1
n
ii
i
n
i
i
X X f
f
18
ộ lệch chuẩn (
)

2
19
Hệ số biến thiên
100
e
e
VX

100VX

20
CÁC THAM SỐ BIỂU THỊ HÌNH DÁNG CỦA THAM SỐ
Cách 1: So sánh 3 chỉ
tiêu đặc trưng.
+)Nếu đường cong phân phối đối xứng thì:
eo
X M M
+)Nếu đường cong phân phối l ch phải thì:
eo
X M M
+)Nếu đường cong phân phối l ch trái thì:
eo
X M M
Cách 2: Tính hệ không
đối xứng.
o
A
XM
K
*Khi
A
K
>0 là phân phối l ch phải.
*Khi
A
K
<0 là phân phối l ch trái.
*Khi
A
K
=0 là phân phối chuẩn đối xứng.
H đối xứng tính ra càng lớn dãy số phân phối c ng ông đối xứng.