
PH N I. M ĐUẦ Ở Ầ
1.1. Lí do ch n đ tài:ọ ề
Phát tri n năng l c t duy sáng t o cho h c sinh là vi c làm r t quanể ự ư ạ ọ ệ ấ
tr ng và c n thi t trong quá trình d y h c, giáo d c h c sinh. Phát tri n tọ ầ ế ạ ọ ụ ọ ể ư
duy sáng t o s giúp h c sinh t tin vào b n thân đ không ng ng khám phá,ạ ẽ ọ ự ả ể ừ
tìm tòi, phát hi n cái m i; sáng t o s giúp h c sinh ch đng ti p thu ki nệ ớ ạ ẽ ọ ủ ộ ế ế
th c, có ngh l c và ni m tin đ chinh ph c nh ng khó khăn trong h c t p.ứ ị ự ề ể ụ ữ ọ ậ
Cao h n t duy sáng t o s giúp h c sinh tìm ra con đng ng n nh t, nhanhơ ư ạ ẽ ọ ườ ắ ấ
nh t đ đt thành công trong h c t p, trong cu c s ng. ấ ể ạ ọ ậ ộ ố
Xu t phát t đc thù c a b môn toán v i s khái quát và tr u t ng cao,ấ ừ ặ ủ ộ ớ ự ừ ượ
s liên k t liên t c các ki n th c toán h c theo t ng năm h c, t ng c p h c.ự ế ụ ế ứ ọ ừ ọ ừ ấ ọ
Đi u đó đòi h i h c sinh không ch c n ph i tích c c, ch đng ti p thu, lĩnhề ỏ ọ ỉ ầ ả ự ủ ộ ế
h i ki n th c m i mà còn ph i bi t v n d ng linh ho t ki n th c đã h c,ộ ế ứ ớ ả ế ậ ụ ạ ế ứ ọ
bi t k t n i nh ng ki n th c cũ đ chi m lĩnh ki n th c m i… Vì l đó vi cế ế ố ữ ế ứ ể ế ế ứ ớ ẽ ệ
đi m i ph ng pháp d y h c trong d y h c môn Toán càng tr nên quanổ ớ ươ ạ ọ ạ ọ ở
tr ng, b c thi t và đó cũng chính là nhi m v c a nh ng ng i giáo viên d yọ ứ ế ệ ụ ủ ữ ườ ạ
Toán.
N i dung hình h c không gian th ng đc xem là n i dung khó h cộ ọ ườ ượ ộ ọ
nh t đi v i h c sinh THPT, khi d y h c ch đ này nhi u giáo viên c mấ ố ớ ọ ạ ọ ủ ề ề ả
th y khó d y, không m y h ng thú nh các ch đ khác c a môn Toán.ấ ạ ấ ứ ư ủ ề ủ
Nguyên nhân quan tr ng d n đn th c tr ng nêu trên là do hình h c khôngọ ẫ ế ự ạ ọ
gian đòi h i m c đ t duy và t ng t ng cao; h c sinh đang quen v i tỏ ứ ộ ư ưở ượ ọ ớ ư
duy v hình h c ph ng nên g p nhi u khó khăn khi làm quen và t duy về ọ ẳ ặ ề ư ề
hình h c không gian. Đ h c t t hình h c không gian h c sinh c n phát huy tọ ể ọ ố ọ ọ ầ ư
duy sáng t o, ng c h c sinh h c t t môn toán nói chung ch đ hình h cạ ượ ọ ọ ố ủ ề ọ
không gian nói riêng thì s góp ph n phát tri n t duy sáng t o. ẽ ầ ể ư ạ
Nh ng lí do nêu trên là c s đ tôi ch n đ tài nghiên c u: ữ ơ ở ể ọ ề ứ “ Phát tri nể
năng l c t duy sáng t o cho h c sinh Trung h c ph thông thông qua m tự ư ạ ọ ọ ổ ộ
s k thu t gi i toán hình h c không gian l p 11”.ố ỹ ậ ả ọ ớ
1.2. M c đích c a đ tàiụ ủ ề
- Nghiên c u ph ng pháp gi ng d y gi i bài t p toán theo h ng hìnhứ ươ ả ạ ả ậ ướ
thành và phát tri n t duy sáng t oể ư ạ cho học sinh.
- D a theo chu n ki n th c k năng hình h c 11 c a B GD-ĐT vàự ẩ ế ứ ỹ ọ ủ ộ
xu t phát t th c ti n gi ng d yấ ừ ự ễ ả ạ hình h c không gian 11, thông qua m t sọ ộ ố
ph ng pháp nh m rèn luy n năng l c t duyươ ằ ệ ự ư cho h c sinh.ọ
1.3. Đi t ng nghiên c uố ượ ứ
Bài t p hình h c không gian trong ch ng I+II SGK hình h c 11 theoậ ọ ươ ọ
ch ng trình c b n và nâng cao.ươ ơ ả
1.4. Ph ng pháp nghiên c u:ươ ứ
Đt v n đ, gi i quy t v n đ.ặ ấ ề ả ế ấ ề
1

PH N 2. N I DUNGẦ Ộ
2.1. C s lí lu n c a đ tài.ơ ở ậ ủ ề
2.1.1. C s toán h c. ơ ở ọ
+ Các đnh nghĩa, đnh lý, tính ch t v hình h c ph ng THCS, hình h cị ị ấ ề ọ ẳ ở ọ
không gian trong SGK Hình h c 11.ọ
+ Các tính ch t v phép chi u song song, phép chi u vuông góc, c th : ấ ề ế ế ụ ể
* Đi v i phép chi u song song các tính ch t sau đây th ng đc số ớ ế ấ ườ ượ ử
d ng khi gi i bài t p toán hình h c:ụ ả ậ ọ
Tính ch t 1:ấ Qua phép chi u song song các y u t sau đây không thayế ế ố
đi (b t bi n):ổ ấ ế
+ T s c a hai đo n th ng n m trên hai đng th ng song song ho cỉ ố ủ ạ ẳ ằ ườ ẳ ặ
trùng nhau.
+ S th ng hàng c a 3 đi m ( ph ng chi u không song song v iự ẳ ủ ể ươ ế ớ
đng th ng ch a 3 đi m đó).ườ ẳ ứ ể
+ Đ dài đo n th ng thu c đng th ng song song v i ph ng chi uộ ạ ẳ ộ ườ ẳ ớ ươ ế
không thay đi, nghĩa là bi n đan AB thành A’B’ và AB = A’B’.ổ ế ọ
Tính ch t 2: ấ
+ Phép chi u song song bi n đng th ng không song song v i ph ngế ế ườ ẳ ớ ươ
chi u thành đng th ng.ế ườ ẳ
+ Bi n trung đi m c a đo n th ng không thu c đng th ng song songế ể ủ ạ ẳ ộ ườ ẳ
v i ph ng chi u thành trung đi m c a đo n th ng.ớ ươ ế ể ủ ạ ẳ
Tính ch t 3:ấ
+ nh c a ba đi m phân bi t qua m t phép chi u song song trùng nhauẢ ủ ể ệ ộ ế
thì ba đi m đó th ng hàng.ể ẳ
+ Phép chi u song song theo hai ph ng không cùng ph ng bi n baế ươ ươ ế
đi m A, B, C l n l t thành thành 3 đi m th ng hàng Aể ầ ượ ể ẳ 1, B1, C1 và A2, B2, C2
thì A, B, C th ng hàng.ẳ
* Đi v i phép chi u vuông góc tính ch t sau đây th ng đc số ớ ế ấ ườ ượ ử
d ng: ụ
Tính ch t:ấ Qua phép chi u vuông góc m t góc vuông có nh là m t gócế ộ ả ộ
vuông khi và ch khi có m t c nh song song ho c thu c m t ph ng chi u,ỉ ộ ạ ặ ộ ặ ẳ ế
c nh còn l i không vuông góc v i m t ph ng chi u.ạ ạ ớ ặ ẳ ế
2.1.2. C s tâm lý h c.ơ ở ọ
Theo các nhà tâm lý h c, con ng i ch b t đu t duy tích c c khi n yọ ườ ỉ ắ ầ ư ự ả
sinh nhu c u c n t duy, t c là khi đng tr c m t khó khăn v nh n th cầ ầ ư ứ ứ ướ ộ ề ậ ứ
c n ph i kh c ph c, m t tình hu ng g i v n đ, hay nói nh Rubinstein: “Tầ ả ắ ụ ộ ố ợ ấ ề ư ư
duy sáng t o luôn luôn b t đu b ng m t tình hu ng g i v n đ”. Vi c gi iạ ắ ầ ằ ộ ố ợ ấ ề ệ ả
bài toán nói chung, gi i toán hình h c không gian nói riêng đt h c sinh đngả ọ ặ ọ ứ
tr c m t khó khăn, khó khăn này có th gi i quy t đc n u h c sinh n mướ ộ ể ả ế ượ ế ọ ắ
v ng đc nh ng ki n th c đã h c và bi t cách v n d ng chúng. Nh v yữ ượ ữ ế ứ ọ ế ậ ụ ư ậ
2

các ph ng pháp gi i toán hình h c không gian chính là nh ng công c h uươ ả ọ ữ ụ ữ
hi u đ h c sinh có ni m tin, có đng l c đ gi i các bài toán hình h c.ệ ể ọ ề ộ ự ể ả ọ
Nh ng ho t đng toán h c nói chung, h at đng hình h c nói riêng sữ ạ ộ ọ ọ ộ ọ ẽ
t o ra nhi u tình hu ng g i v n đ t đó t o cho h c sinh nhu c u t duyạ ề ố ợ ấ ề ừ ạ ọ ầ ư
hình h c, t duy toán h c. Theo c s tâm lý h c đã đc các nhà tâm lý h cọ ư ọ ơ ở ọ ượ ọ
k t lu n và đã đc ki m ch ng trong th c ti n giáo d c thì nh ng nhu c uế ậ ượ ể ứ ự ễ ụ ữ ầ
t duy nêu trên s là c s đ h c sinh ti p thu, lĩnh h i ki n th c hình h cư ẽ ơ ơ ể ọ ế ộ ế ứ ọ
m i, ki n th c toán h c m i.ớ ế ứ ọ ớ
2.1.3. C s giáo d c h c.ơ ở ụ ọ
Ho t đng nh n th c toán h c c a h c sinh đc hi u “ là quá trình tạ ộ ậ ứ ọ ủ ọ ượ ể ư
duy n t i lĩnh h i các tri th c toán h c, n m đc ý nghĩa c a các tri th cẫ ớ ộ ứ ọ ắ ượ ủ ứ
đó, xác đnh đc các m i liên h nhân qu và các m i liên h khác c a cácị ượ ố ệ ả ố ệ ủ
đi t ng toán h c đc nghiên c u ( khái ni m; quan h ; quy lu t toán h c;ố ượ ọ ượ ứ ệ ệ ậ ọ
…); t đó h c sinh v n d ng đc tri th c toán h c gi i quy t các v n đừ ọ ậ ụ ượ ứ ọ ả ế ấ ề
th c ti n” .ự ễ
M c tiêu ch y u c a vi c phát tri n ho t đng nh n th c trong d yụ ủ ế ủ ệ ể ạ ộ ậ ứ ạ
h c toán là phát tri n trí tu và nhân cách c a h c sinh. đây s phát tri n tríọ ể ệ ủ ọ Ở ự ể
tu đc hi u là s thay đi v ch t trong ho t đng nh n th c. S bi n điệ ượ ể ự ổ ề ấ ạ ộ ậ ứ ự ế ổ
đó đc đc tr ng b i s thay đi c u trúc cái đc ph n nh và ph ngượ ặ ư ở ự ổ ấ ượ ả ả ươ
th c ph n ánh chúng. Nói nh v y đng nghĩa v i phát tri n trí tu là sứ ả ư ậ ồ ớ ể ệ ự
th ng nh t gi a vi c vũ trang tri th c và vi c phát tri n m t cách t i đaố ấ ữ ệ ứ ệ ể ộ ố
ph ng th c ph n ánh chúng. Trong s th ng nh t đó d n đn làm thay điươ ứ ả ự ố ấ ẫ ế ổ
c u trúc b n thân h th ng tri th c (m r ng c i ti n, b sung, c u trúc l i)ấ ả ệ ố ứ ở ộ ả ế ổ ấ ạ
làm cho h th ng tri th c ngày càng thêm sâu s c và ph n ánh đúng b n ch t,ệ ố ứ ắ ả ả ấ
ti p c n d n v i chân lí và đi u ch nh, m r ng các ph ng th c ph n ánh,ế ậ ầ ớ ề ỉ ở ộ ươ ứ ả
đôi khi đi đn xóa b nh ng ph ng th c ph n ánh cũ đ hình thành nh ngế ỏ ữ ươ ứ ả ể ữ
ph ng th c ph n ánh m i h p lí h n, sáng t o h n, phù h p v i quy lu t tươ ứ ả ớ ợ ơ ạ ơ ợ ớ ậ ự
nhiên và xã h i. Phát tri n trí tu đc hi u c th qua phát tri n các năngộ ể ệ ượ ể ụ ể ể
l c trí tu bao g m năng l c thu nh n thông tin toán h c; năng l c ch bi nự ệ ồ ự ậ ọ ự ế ế
thông tin toán h c; năng l c t duy logic, tu duy bi n ch ng, t duy phê phán,ọ ự ư ệ ứ ư
t duy đnh l ng; năng l c khái quát nhanh chóng và r ng rãi các đi t ng,ư ị ượ ự ộ ố ượ
các quan h , các m i liên h trong toán h c; có tính m m d o trong quá trìnhệ ố ệ ọ ề ẻ
t duy; năng l c thay đi nhanh chóng chuy n h ng suy nghĩ t d ng nàyư ự ổ ể ướ ừ ạ
sang d ng khác.ạ
Nh v y thông qua ho t đng nh n th c toán h c nói chung, ho t đngư ậ ạ ộ ậ ứ ọ ạ ộ
nh n th c v hình h c không gian nói riêng s nh m th c hi n m c tiêu giáoậ ứ ề ọ ẽ ằ ự ệ ụ
d c nhân cách cho h c sinh; giáo d c t duy phê phán; cách gi i quy t v n đụ ọ ụ ư ả ế ấ ề
sáng t o; cách x lí thông tin… trong cu c s ng th c ti n.ạ ử ộ ố ự ễ
2.2. Th c tr ng c a đ tài.ự ạ ủ ề
Qua th c ti n quá trình d y h c đng th i thông qua vi c tìm hi u, đi uự ễ ạ ọ ồ ờ ệ ể ề
tra t giáo viên và h c sinh các tr ng THPT trên đa bàn huy n Qu ngừ ọ ở ườ ị ệ ả
3

X ng; t ng h p các thông tin có đc khi tìm hi u trên các ph ng ti nươ ổ ợ ượ ể ươ ệ
thông tin đi chúng tôi nh n th y trong vi c d y và h c ch đ hình h cạ ậ ấ ệ ạ ọ ủ ề ọ
không gian t n t i nh ng th c tr ng sau:ồ ạ ữ ự ạ
+ Đi v i giáo viên:ố ớ
- Nhi u giáo viên c m th y ít h ng thú khi d y ch đ hình h c khôngề ả ấ ứ ạ ủ ề ọ
gian d n đn ch a th c s tìm tòi, đi m i ph ng pháp d y h c phù h pẫ ế ư ự ự ổ ớ ươ ạ ọ ợ
v i đi t ng h c sinh.ớ ố ượ ọ
- Ch a phát huy hi u qu tính ch đng, sáng t o c a h c sinh. Ítư ệ ả ủ ộ ạ ủ ọ
khuy n khích h c sinh tìm tòi, khám phá nh ng cách gi i m i.ế ọ ữ ả ớ
- Ch a xây d ng đc h th ng bài t p đa d ng, phù h p v i t ng điư ự ượ ệ ố ậ ạ ợ ớ ừ ố
t ng h c sinh ( ch y u các bài t p đc l y trong SGK).ượ ọ ủ ế ậ ượ ấ
+ Đi v i h c sinh:ố ớ ọ
- Đa s c m th y khó d n đn ng i, không h ng thú khi h c hình khôngố ả ấ ẫ ế ạ ứ ọ
gian. Cá bi t có nhi u đi t ng h c sinh b h n không h c ph n hình h cệ ề ố ượ ọ ỏ ẵ ọ ầ ọ
không gian mà ch t p chung vào các ch đ khác.ỉ ậ ủ ề
- T t ng xem nh ch đ hình h c không gian c a nhi u h c sinh xu tư ưở ẹ ủ ề ọ ủ ề ọ ấ
phát t vi c nh n th c ch đ này ch chi m m t ph n nh trong các kì thiừ ệ ậ ứ ủ ề ỉ ế ộ ầ ỏ
đi h c, nhi u h c sinh cho r ng có th h c t t các ch đ khác đ khi thi sạ ọ ề ọ ằ ể ọ ố ủ ề ể ẽ
bù cho ch đ hình h c không gian.ủ ề ọ
- Đa s h c sinh ch a ý th c sâu s c vi c h c t t hình h c không gian số ọ ư ứ ắ ệ ọ ố ọ ẽ
góp ph n phát tri n t duy sáng t o t đó góp ph n h c t t các ch đ khác,ầ ể ư ạ ừ ầ ọ ố ủ ề
các môn h c khác.ọ
- Đa s h c sinh ít ch đng t duy khi gi i toán hình h c không gian,ố ọ ủ ộ ư ả ọ
m t s n m đc các ph ng pháp gi i toán hình h c không gian nh ng sộ ố ắ ượ ươ ả ọ ư ử
d ng ch a linh ho t, thi u sáng t o.ụ ư ạ ế ạ
2.3. Các bi n pháp gi i quy t v n đ.ệ ả ế ấ ề
Nh m nâng cao k t qu h c t p và góp ph n phát tri n t duy sáng t oằ ế ả ọ ậ ầ ể ư ạ
cho h c sinh thông qua d y h c ch đ hình h c không gian l p 11 tôi đã th cọ ạ ọ ủ ề ọ ớ ự
hi n các n i dung chính nh sau:ệ ộ ư
+ Công tác chu n b : ẩ ị
- Đánh giá đi t ng h c sinh; so n bài; xây d ng h th ng bài t p đaố ượ ọ ạ ự ệ ố ậ
d ng nh ng phù h p v i n i dung ch ng trình và đi t ng h c sinh.ạ ư ợ ớ ộ ươ ố ượ ọ
- Ngoài các ti t d y chính theo phân ph i ch ng trình tùy theo m c đế ạ ố ươ ứ ộ
nh n th c c a h c sinh đ xây d ng k ho ch d y t ch n, b i d ng hayậ ứ ủ ọ ể ự ế ạ ạ ự ọ ồ ưỡ
ph đo cho h c sinh v ch đ hình h c không gian.ụ ạ ọ ề ủ ề ọ
- Chu n b các đ dùng h c t p c n thi t ( các tài li u, mô hình hình h c,ẩ ị ồ ọ ậ ầ ế ệ ọ
các ph n m m h tr d y h c hình h c không gian….).ầ ề ỗ ợ ạ ọ ọ
+ T ch c th c hi n:ổ ứ ự ệ
- D y h c theo ch ng trình, k ho ch đã đ ra.ạ ọ ươ ế ạ ề
- Trang b cho h c sinh các ph ng pháp gi i toán hình h c không gianị ọ ươ ả ọ
thông qua các bài t p, ví d đi n hình.ậ ụ ể
4
- Đa ra nh ng bài t p ôn t p, các bài t p phát tri n t duy hình h c phùư ữ ậ ậ ậ ể ư ọ
h p v i đi t ng h c sinh. ợ ớ ố ượ ọ
- Tích c c đi m i ph ng pháp d y h c nh : Tăng c ng ho t đngự ổ ớ ươ ạ ọ ư ườ ạ ộ
theo nhóm, s d ng các mô hình tr c quan… Khuy n khích h c sinh gi i toánử ụ ự ế ọ ả
hình h c không gian b ng nhi u cách. Đt ra các câu h i, các v n đ đòi h iọ ằ ề ặ ỏ ấ ề ỏ
h c sinh ph i tích c c t duy đ tr l i.ọ ả ự ư ể ả ờ
- Giao bài t p v nhà phù h p v i đi t ng h c sinh, chú tr ng các bàiậ ề ợ ớ ố ượ ọ ọ
t p đòi h i h c sinh ph i ch đng và sáng t o. ậ ỏ ọ ả ủ ộ ạ
- Ki m tra, đánh giá, phân lo i h c sinh b ng nhi u hình th c ( c đnhể ạ ọ ằ ề ứ ả ị
tính và đnh l ng).ị ượ
C th trong quá trình d y h c ch đ hình h c không gian l p 11 tôi đãụ ể ạ ọ ủ ề ọ ớ
xác đnh và th c hi n hi u qu m t s bi n pháp sau đây:ị ự ệ ệ ả ộ ố ệ
2.3.1. Bi n pháp 1: V n d ng ph ng pháp tách các b ph n ph ngệ ậ ụ ươ ộ ậ ẳ
ra kh i không gian.ỏ
Khi gi i quy t các bài toán hình h c không gian h c sinh g p ph i nhi uả ế ọ ọ ặ ả ề
khó khăn h n so v i các bài toán hình h c ph ng nh : Vi c t ng t ng, hìnhơ ớ ọ ẳ ư ệ ưở ượ
dung đ tìm các m i liên h gi a các y u t hình h c ( nh quan h gi a cácể ố ệ ữ ế ố ọ ư ệ ữ
đng th ng, m t ph ng…); vi c v hình đ bi u di n hình không gian trongườ ẳ ặ ẳ ệ ẽ ể ể ễ
m t ph ng… Khó khăn này s nh h ng đn vi c v n d ng lí thuy t đặ ẳ ẽ ả ưở ế ệ ậ ụ ế ể
gi i quy t các bài toán hình h c không gian. Đ kh c ph c khó khăn này vi cả ế ọ ể ắ ụ ệ
tách các b ph n ph ng ra kh i không gian s giúp h c sinh quy m t bài toánộ ậ ẳ ỏ ẽ ọ ộ
ph c t p v gi i quy t bài toán đn gi n h n, d hi u và d th c hi n h n. ứ ạ ề ả ế ơ ả ơ ễ ể ễ ự ệ ơ
a) Các ví d minh h a.ụ ọ
Ví d 1:ụ Cho t di n ABCD có tr ng tâm G, AG c t (BCD) t i A’. Ch ngứ ệ ọ ắ ạ ứ
minh r ng A’ là tr ng tâm c a tam giác BCD ( Đng th ng đi qua m t đnhằ ọ ủ ườ ẳ ộ ỉ
và tr ng tâm c a t di n đi qua tr ng tâm c a m t đi di n v i đnh y).ọ ủ ứ ệ ọ ủ ặ ố ệ ớ ỉ ấ
Đnh h ng ph ng pháp và l i gi i:ị ướ ươ ờ ả
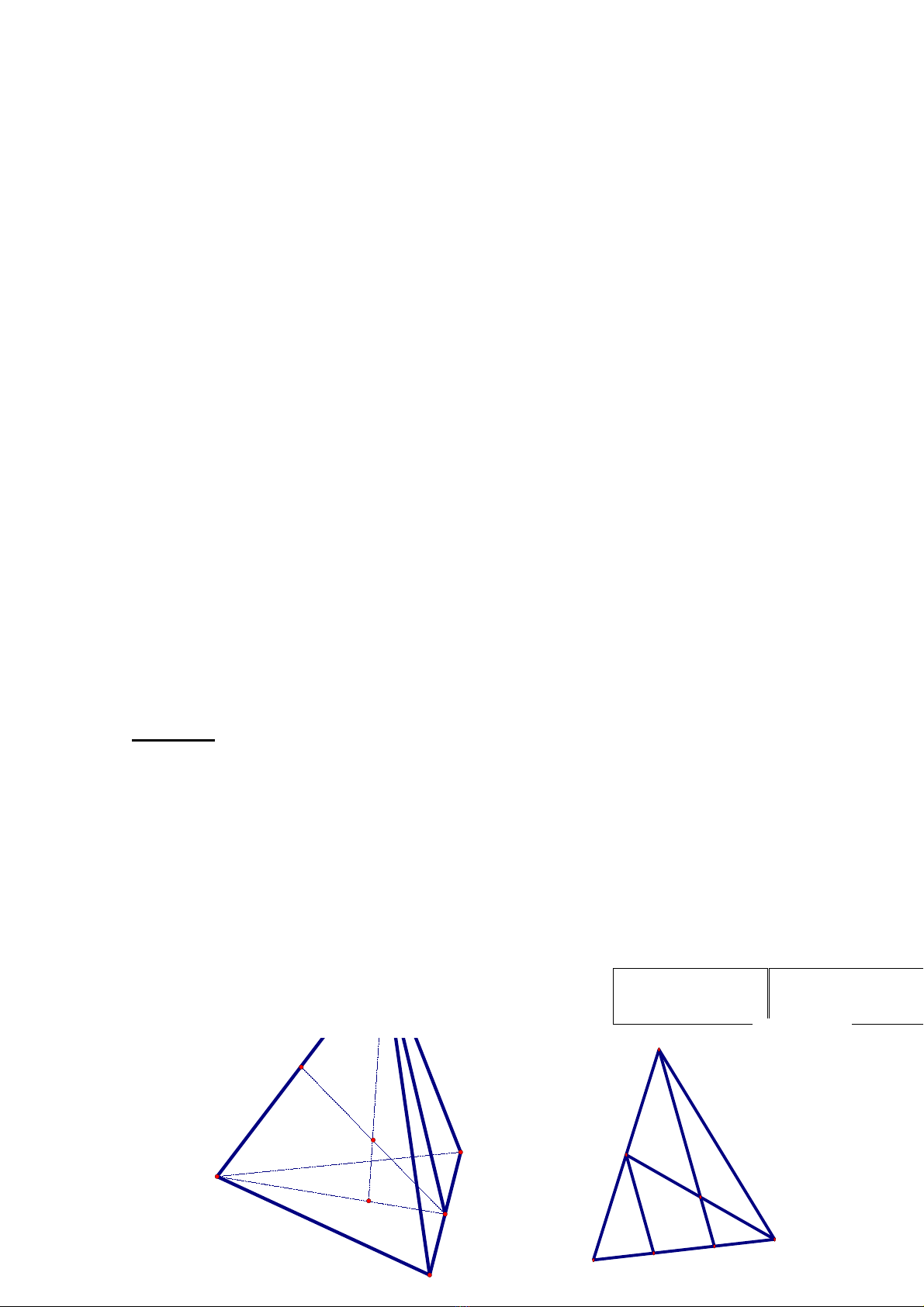
B ng vi c bóc tách các y u t ph ng ra kh i không gian, bài toán trênằ ệ ế ố ẳ ỏ
đc chuy n thành bài toán hình h c ph ng sau đây:ượ ể ọ ẳ
Cho tam giác ABN, M là trung đi m c a AB, G là trung đi m c a MN,ể ủ ể ủ
AG c t c nh BN t i A’. Ch ng minh r ng BA’ = 2 A’N ắ ạ ạ ứ ằ .
5
A'
G
N
M
D
C
B
G
D
A'
M
N
B
A
Không gian M t ph ngặ ẳ
A


























