PHÉP BIẾN ĐỔI KHÓA – HÀM BĂM
Băm là phương pháp rất thích hợp để cài đặt tập hợp có số phần tử lớn và thời
gian cần thiết để thực hiện các phép toán từ điển, ngay cả trong trường hợp xấu
nhất, là tỉ lệ với cỡ của tập hợp.
Chúng ta sẽ đề cập tới hai phương pháp băm khác nhau. Một gọi là băm mở cho
phép sử dụng một không gian không hạn chế để lưu giữ các phần tử của tập hợp.
Phương pháp băm khác được gọi là băm đóng sử dụng một không gian cố định do
đó tập hợp được cài đặt phải có cỡ vượt qua không gian cho phép
$1. Khái niệm băm và hàm băm.
1.1. Băm mở và hàm băm.
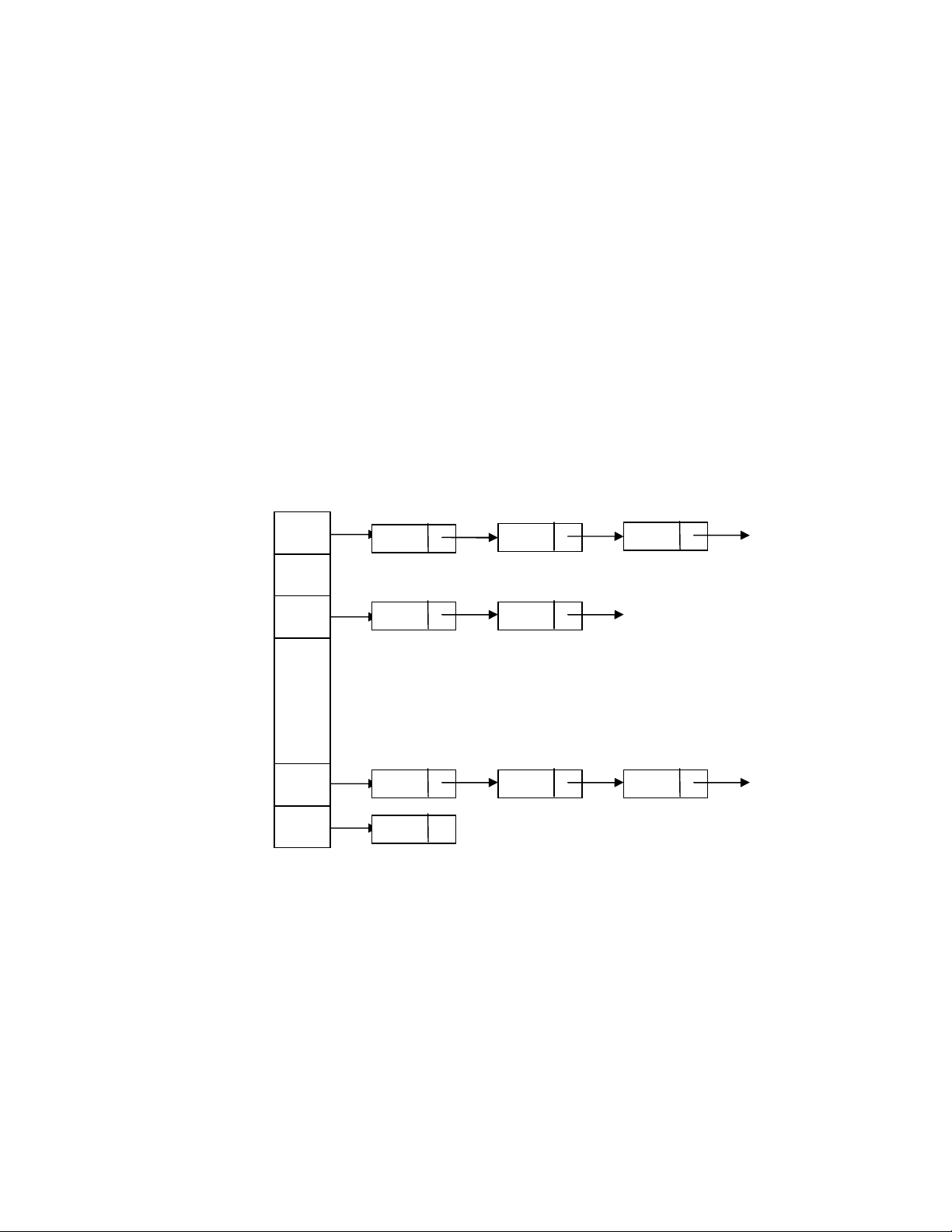
a. Băm mở. Nội dung cơ bản của băm mở là phân chia tập hợp đã cho thành một
số cố định các lớp. Chẳng hạn ta muốn phân thành N lớp được đánh số 0,1,..,N-1.
Ta sử dụng mảng T với chỉ số chạy từ 0 đến N-1. Mối thành phần T[i] cúa mảng
được nói đến như một rổ đựng các phần tử của tập hợp thuộc lớp thứ i. Các phần
tử của tập hợp thuộc mỗi lớp tổ chức dưới dạng một danh sách liên kết. Do T[i] sẽ
chứa con trỏ trỏ đến danh sách của lớp i.
b. Bảng băm. Ta gọi mảng T mà mỗi phần tử của nó như là một rổ đựng các phần
tử của tập hợp thuộc lớp tương ứng là bảng băm.
Việc phân chia các phần tử của tập hợp vào các lớp được thực hiện bởi hàm băm
h.
c. Hàm băm. Nếu x là một giá trị khoá của phần tử nào đó của tập hợp thì h(x) là
chỉ số nào đó của mảng T và ta gọi h(x) là giá trị băm (hash value) của x. Như vậy h
là ánh xạ từ tập hợp các khoá K vào tập hợp { 0,1,…,N-1}.
$.2. Các phương pháp lựa chọn, thiết kế hàm băm và giải quyết va chạm.
2.1. Các phương pháp lựa chọn, thiết kế hàm băm
Có hai tiêu chuẩn chính để lựa chọn hàm băm. Trước hết nó phải cho phép tính
được dễ dàng và nhanh chóng giá trị băm của mỗi khoá. Thứ hai, nó phải phân bố
đều các khóa vào các rổ. Trên thực tế tiêu chuẩn thứ hai rất khó được thực hiện.
Sau đây chúng ta đưa ra một số phương pháp thiết kế hàm băm.
a. Phương pháp cắt bỏ.
Giả sử khoá là số nguyên (nếu khoá không phải là số nguyên, ta xét đến các mã số
của chúng). Ta sẽ bỏ đi một phần nào đó của khóa, và lấy phần còn lại lám giá trị
băm của khoá. Chẳng hạn nếu khoá là các số nguyên gồm 10 chữ số và bảng băm
gồm 1000 thành phần, khi đó ta có thể lấy chữ số thứ nhất, thứ ba và thứ bảy từ
bên trái làm giá trị băm. Ví dụ: h(7103592810) = 720.
Phương pháp cắt bỏ rất đơn giản nhưng nó thường không phân bố đều các khoá.
b. Phương pháp gấp.
Giả sử khoá là số nguyên. Ta phân chia khóa thành một số phần, sau đó kết hợp
các phần lại bằng một cách nào đó (phép cộng hoặc phép nhân) để nhận giá trị
băm. Nếu khoá là số nguyên 10 chữ số ta phân thành các nhóm ba ba hai hai chữ
số từ bên trái, cộng các nhóm với nhau sau đó cắt cụt nếu cần thiết, ta sẽ nhận
được giá trị của hàm băm. Ví dụ: số 7103592810 được biến đổi thành
710+359+28+10 = 1107, do đó ta có giá trị băm là 107.
Vì mọi thông tin trong khoá đều được phản ánh vào giá trị băm, nên phương pháp gấp
cho phân bố đều các khoá hơn phương pháp cắt bỏ.
c. Phương pháp sử dụng phép toán lấy dư.
Giả sử khoá là số nguyên và ta muốn chia tập hợp các khoá thành n lớp. Chia số
nguyên cho n rồi lấy phần dư làm giá trị băm. Điều này trong Pascal được thực
hiện bằng phép toán mod. Tính phân bố đều các khoá của hàm băm được xác định
bằng phương pháp này phụ thuộc nhiều vào việc chọn n. Tốt nhất chọn n là số
nguyên tố. Chẳng hạn thay cho việc chọn n = 1000 ta sẽ chọn n = 997 hoặc n =
1009.
Ví dụ viết một hàm băm trong Pascal để băm các khoá là các xâu kí tự có độ dài 10
thành các giá trị từ 0…n-1.
Type keytype = string[10];
Function h(x: keytype):0..n-1;
Var
i, sum:integer ;
Begin
Sum:=0;
For i=1 to 10 do
Sum=sum + ord(x[i]);
h:= sum mod n;
end.
Trong hàm băm trên, ta đã chuyển đổi các xâu kí tự thánh các số nguyên bằng
cách lấy tổng số của các mã số của từng kí tự trong xâu dùng hàm ord(c) để lấy mã
số của kí tự c.
2.2. Bảng băm đóng.
Trong bảng băm mở, mỗi thành phần T[i] của bảng lưu trữ con trỏ trỏ tới danh sách
các phần tử của tập hợp được đưa vào lớp thứ i (i = 0,…,N-1).
a. Băm đóng. Khác với bảng băm mở, trong bảng băm đóng, mỗi phần tử của tập
lưu giữ trong chính các thành phần T[i] của mảng. Do đó ta có thể khai báo kiểu dữ
liêụ từ điển được cài đặt bởi bảng băm đóng như sau:
0
1
2
Type Dictionary = array [0..N-1] of keytype;
Keytype là kiểu dữ liệu của khoá của các phần tử trong từ điển.
2.3. Phân tích, đánh giá và minh họa phương pháp băm.
a. Phân tich đánh giá. Trong tất cả những thuật toán được xét từ trước tới nay, việc
định vị một mục được xác định bởi một dãy các so sánh. Trong mỗi trường hợp,
mục cần tìm được so sánh nhiều lần với các mục ở những vị trí nào đó trong cấu
trúc. Đối với nhóm n mục, phép tìm kiếm tuyến tính đòi hỏi O(n) lần so sánh, trong
khi đó phép tìm kiếm nhị phân chỉ cần O(log n) lần so sánh. Trong một số trường
hợp, những thuật toàn này thực hiện còn quá chậm. Ví dụ, bảng các kí hiệu được
lập bởi bộ dịch lưu trữ các định danh và những thông tin về chúng. Vận tốc xây
dựng và tìm kiếm trong bảng này quyết định vận tốc dịch. Một cấu trúc dữ liệu thực
hiện tìm kiếm nhanh hơn, được gọi là bảng băm (hash T), trong đó vị trí cuả một
mục được xác định trực tiếp bằng một hàm của chính nó chứ không phải bằng một
dãy các so sánh thử và sai (trial-and-error). Thời gian gian cần thiết để định vị một
mục trong bảng băm trong trường hợp tốt nhất là O(1), nghĩa là nó là một hằng số
và không phụ thuộc vào số các mục được lưu trữ.
b. Ví dụ minh họa. Để minh hoạ, giả sử rằng cần lưu trữ 25 số nguyên trên đoạn
0..999 trong bảng băm. Có thể cài đặt bảng băm này bằng một mảng T các số
nguyên được đánh chỉ số trên đoạn 0..999, trong đó mỗi phần tử của mảng được
khởi động tại một giá trị câm nào đó, chẳng hạn như tại 1. Nếu ta dùng mỗi số
nguyên i trong tập hợp đó làm chỉ số, nghĩa là nếu ta lưu trữ i trong T[i], ta có thể
định vị một số nguyên number cho trước chỉ bằng cách kiểm tra T[number]
=number hay không. Hàm h được định nghĩa bởi h(i)=i xác định vị trí của mục i
trong bảng băm.
Hàm băm trong vị dụ này thực hiện tìm kiếm một cách lý tưởng vì thời gian cần
thiết để tìm kiếm một giá trị cho trước trong báng là hằng số; chỉ cần thử một vị trí.
Như vậy, sơ đồ này hiêu quả về tính thời gian, nhưng không hiệu quả về không
gian, chỉ 25 trong số 1000 vị trí khả dĩ được dùng để lưu trư các mục còn 975 vị trí
còn lại không được dùng do đó đã lãng phí 97,5% không gian, chỉ dùng 2,5%.
Vì có thể lưu trữ 25 giá trị ở 25 vị trí ta có thể sử dụng tốt hơn bằng cách dùng
mảng T được đánh chỉ số trên đoạn từ 0 đến 24. Dĩ nhiên là không thể dùng hàm
băm ban đầu h(i)=i được nữa. Thay vào đó ta có thể dùng: h(i)=i mod 25
Vì hàm này luôn luôn có miền giá trị là những số nguyên trên đoạn từ 0 đến 24.
Như vậy số nguyên 52 sẽ được lưu trữ ở T[2] vì h(52)= 52 mod 25 = 2. Tương tự
với các số nguyên 129; 500 ; 73; 49 sẽ được lưu tại các vị trí 4, 0, 23 và 24 theo
thứ tự đó.
T[0]
T[1]
T[2]
T[3]
T[4]
T[5]
.
.
T[23]
T[24]
Với ví dụ trên nếu lấy hàm h[i]:=i mod 25 thì sẽ xẩy ra hiện tượng gọi là sự va
chạm. vì nếu 77 được lưu trữ, nó sẽ được đặt vào vị trí h(77)= 77 mod 25 = 2,
nhưng vị trí này đã bị chiếm bởi 52. Cũng bằng cách đó, nhiều giá trị khác có thể
trùng vào một vị trí cho trước,ví dụ,2,27,102 và trong thực tế tất cả các số nguyên
dạng 25k + 2 đều được lưu trữ tại vị trí 2. Dĩ nhiên là cần phải có một cách nào đó
để giải quyết những va chạm này.
$3. Các phương pháp xử lý va chạm.
3.1.Phương pháp thăm dò tuyến tính.
a. Nội dung. Trong sơ đồ này, phép tuyến tính trong bảng bắt đầu từ chỗ có va
chạm và tiếp tục dò đền khi tìm thấy một khe trống có thể lưu trữ được, va chạm
với giá trị 52 ở vị trí 2, một cách đơn giản là ta đặt 77 ở giá trị 3; để chèn 102,
500
-1
52
-1
129
-1
.
.
273
49