( 45 tit )
Chng 1 : Phép tính vi phân hàm mt bin
Chng 2 : Phép tính tích phân hàm mt bin
Chng 3 : Lý thuyt chui
Chng 4 : Phép tính vi phân hàm nhiu bin
Chng 5 : ng dng ca hàm nhiu bin
TÀI LIU THAM KHO
[1] Toán hc cao cp, tp 2&3, Nguyn ình Trí (ch biên),
NXB Giáo dc, 2009
[2] Toán cao cp, Gii tích hàm mt bin & Gii tích hàm
nhiu bin,  Công Khanh (ch biên), NXB HQG
TP.HCM, 2010
Chng 1. Phép tính vi phân hàm mt bin
1.1. Các khái nim c bn v hàm s mt bin
1.1.1. nh ngha.
Cho X và Y là các tp hp khác rng. Mt ánh xt tp X vào tp
Y là mt quy tc t tng ng mi phn t ca X vi duy nht mt
phn t ca Y. Ký hiu là
trong ó: y c gi là nh ca x qua ánh x f
x c gi là to nh ca y qua ánh x f
VD.
là ánh x; không là ánh x (vì s 0
không có nh)
2
f :
x x
f :
1
x
x
f : X Y
x y f x
Nu ta có tp hp
có không quá mt phn t (hoc )
thì f là n ánh.
Nu ta có tp hp (hoc ) thì
f là toàn ánh.
Nu f va n ánh va toàn ánh thì f là song ánh
. Tc vi mi
, tn ti duy nht mt phn t sao cho f(x) = y.
VD. là song ánh
không n ánh, không toàn ánh
1 2 1 2
f x f x x x
f X Y
3
f :
x x
2
f :
x x
1
f y
y Y
1
f y x X f x y
y Y
y Y
x X
Cho là song ánh. Khi ó, vi mi , tn ti
duy nht mt phn t sao cho f(x) = y. Ánh x
t tng ng phn t y vi ngh ch nh x ca nó c gi là ánh
x ngcca f.
Vy:
(Ánh x ngc ca f c!ng là song ánh)
Cho hai tp khác rng . Ánh x c
gi là mt hàm s. Ký hiu y = f(x).
Tp X c gi là tp xác nh ca f, ký hiu Df.
Tp c gi là min giá tr ca f.
X , Y
f : X Y
Y y f x x X
f : X Y
y Y
x X
1
f : Y X
1
y Y , f y x f x y
1
f
1.1.2. Hàm s ngc
nh ngha. Cho song ánh . Ánh x ngc ca f là
gi là hàm s ngcca hàm y = f(x), và vit là
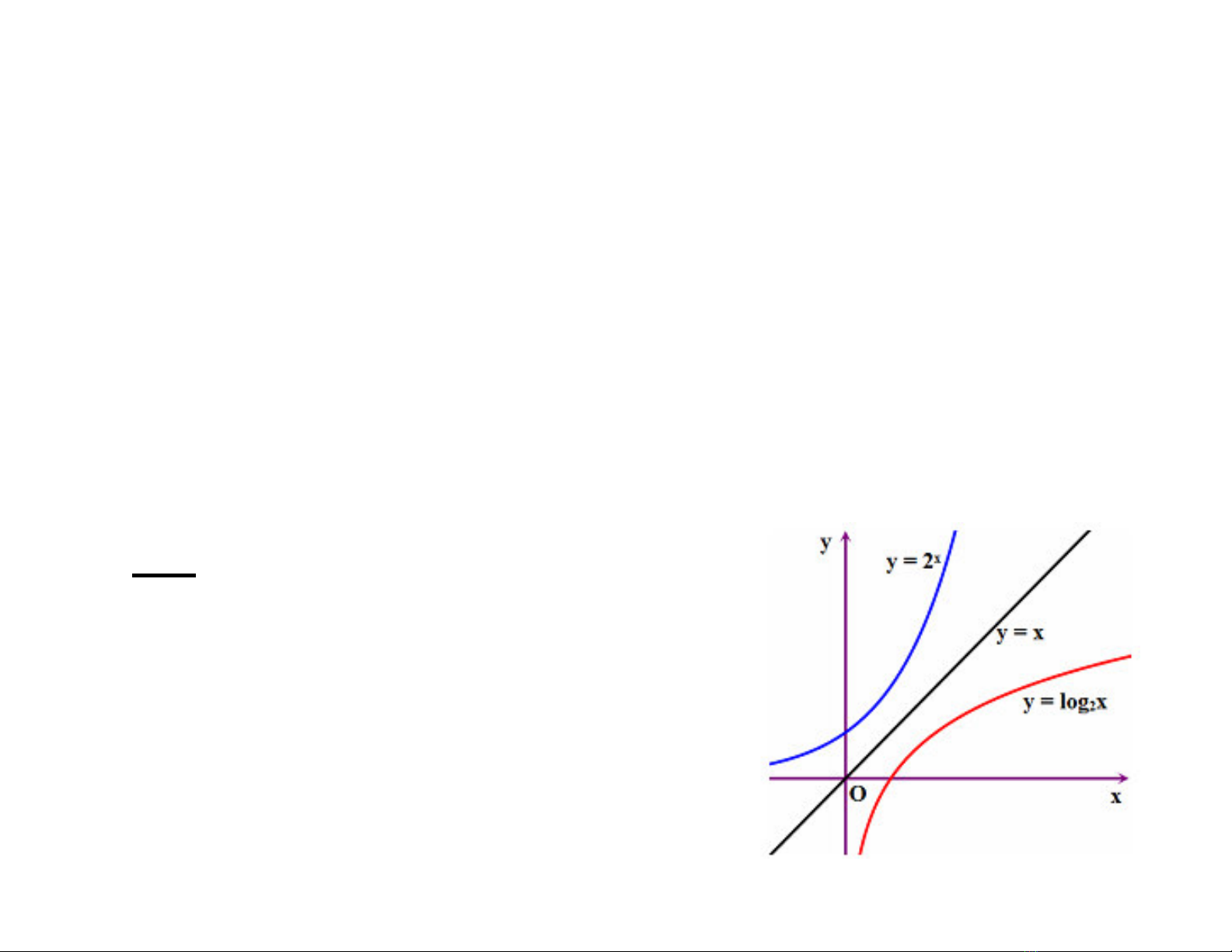
Nu là hàm s ngc ca hàm y = f(x) thì  th
ca chúng i xng qua "ng th#ng y = x.
VD.
f : X Y
1
f
x y ; y Y
1
y f x
x 1
2
f x 2 f x log x ; x 0
>