www.laisac.page.tl
P
PH
HƯ
ƯƠ
ƠN
NG
GP
PH
HÁ
ÁP
PT
TÌ
ÌM
MG
GI
IÁ
ÁT
TR
RỊ
ỊL
LỚ
ỚN
NN
NH
HẤ
ẤT
T,
,G
GI
IÁ
ÁT
TR
RỊ
ỊN
NH
HỎ
ỎN
NH
HẤ
ẤT
TC
CỦ
ỦA
A
B
BI
IỂ
ỂU
UT
TH
HỨ
ỨC
CC
CH
HỨ
ỨA
AH
HA
AI
IB
BI
IẾ
ẾN
N.
.
NguyễnTrungNghĩa
I- S DNG TP GIÁ TR:
• Bài toán: Cho các s thc x, y tha mãn iu kin
( )
=. Tìm giá tr ln nht và
giá tr nh nht (nu có) ca biu thc
( )
=.
• Phng pháp gii chung: Gi T là tp giá tr ca P, khi ó ∈ khi và ch khi h
phương trình sau có nghim:
( )
( )
=
=
(1)
• Sau ó tìm các giá tr ca m  h (1) có nghim (thng là a v iu kin có nghim
ca mt phơng trình bc hai) ri suy ra tp giá tr T ca P, t ó suy ra giá tr ln nht
và giá tr nh nht (nu có) ca biu thc
( )
=.
• Mt s ví d minh ha:
Ví d 1: ( thi i hc d b khi A nm 2006)
Gii: t
 = + + và
 = − − .
Gi T là tp giá tr ca B, khi ó ∈ khi và ch khi h sau có nghim:


+ + ≤
− − =
(1)
• Nu y = 0 thì = ≤ , lúc ó
− − < ≤ = ≤ < − (pcm).
• Nu ≠ thì t =, khi ó

= + + = + + >
nên:


− − − −
= =
+ + + + .
t
( ) ( )

− −
= ⇔ − + + + + =
+ + .
H (1) có nghim ⇔ Phương trình (2) có nghim
( ) ( )( )
⇔ ∆ = + − − + ≥
− − −
⇔ ≤ ≤ .
Do ó:
− − −
≤ ≤ , mt khác < ≤ nên − − ≤ ≤ − .
Cho hai s thc x, y thay i và tha mãn  + + ≤ . Chng minh rng:

− − ≤ − − ≤ −
Vy tp giá tr ca P là 
= − − −
nên suy ra pcm.
Ví d 2: ( thi hc sinh gii quc gia nm 2005)
Gii: KX:
≥ − và ≥ − .
Gi T là tp giá tr ca K. Ta có ∈ khi và ch khi h phương trình sau có nghim:

− + = + −
+ =
t = + và = + thì  ≥ ≥ và h (1) tr thành:
( )

+ =
+ =
⇔ ⇔
+ = +
= − −
u, v là hai nghim ca phương trình:
 

− + − − = ⇔ − + − − =
(2).
Do ó h (1) có nghim (x , y) sao cho
≥ − và ≥ − khi và ch khi phương trình (2) có hai
nghim không âm và iu kin là:
( )
 




∆ = − − − ≥
+
= ≥ ⇔ ≤ ≤ +
− −
= ≥
.
Do ó 
+
= +
.
Vy giá tr nh nht ca K là 
+ và giá tr ln nht ca K là +.
Cho hai s thc x, y thay i và tha mãn h thc − + = + − . Tìm giá tr
ln nht và giá tr nh nht ca biu thc = + .
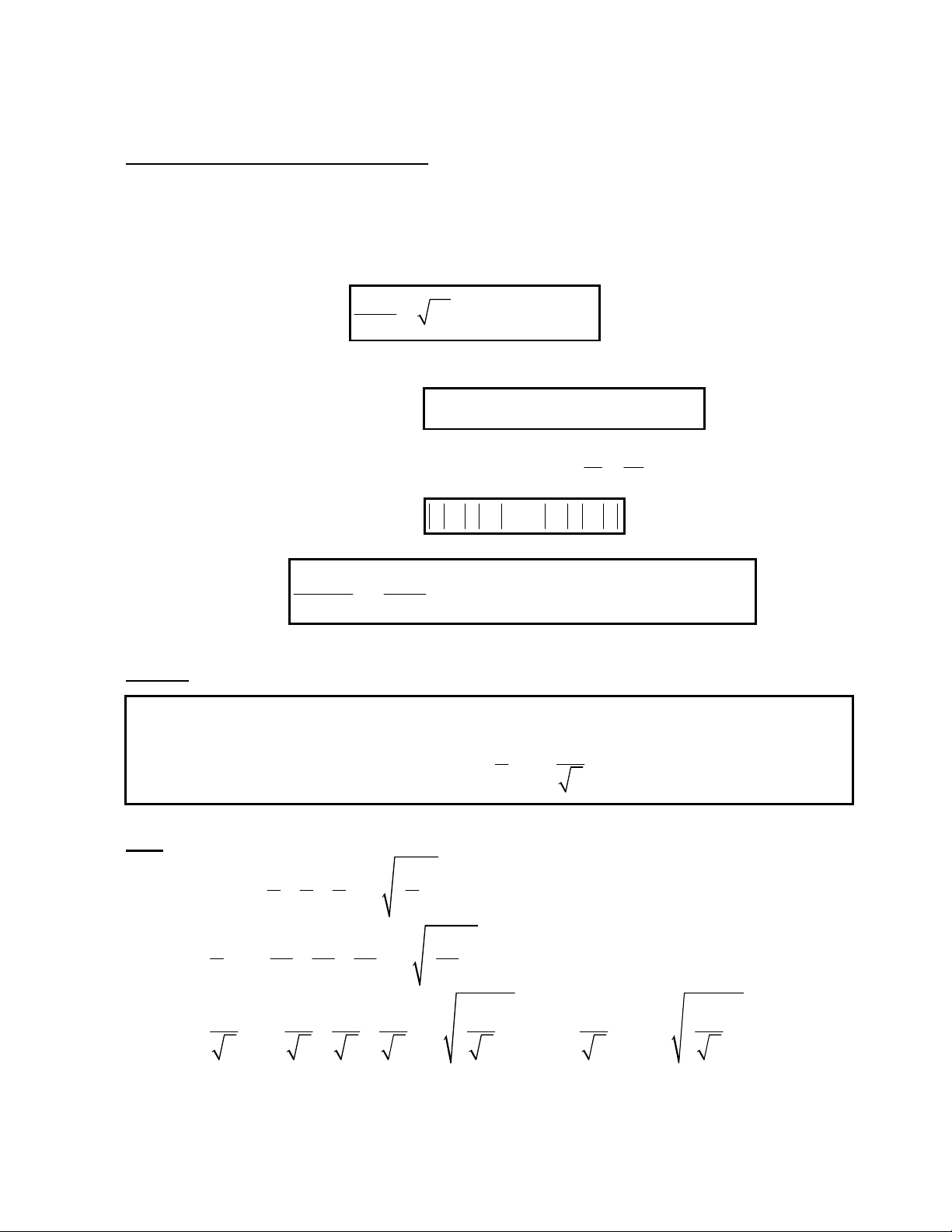
II- S DNG BT NG THC:
• Phng pháp chung: Mu cht ca phơng pháp bt ng thc là phi d oán c
biu thc s t giá tr ln nht , giá tr nh nht ti nhng giá tr nào ca bin s  t
ó có nhng cách phân tích, ánh giá thích hp.
• Mt s bt ng thc cn nh:
BT Cô-si:

+≥ (vi ≥ ≥ )
ng thc xy ra khi và ch khi =.
BT Bunhiacopxki:
( )
( )( )
+ ≤ + +
ng thc xy ra khi và ch khi
=.
BT v tr tuyt i: − ≤ − ≤ +
BT
+ +
≥
(vi n nguyên dương và ≥ ≥ )
• Mt s ví d minh ha:
Ví d 1: ( thi i hc d b khi A nm 2005)
Gii:
•

+ = + + + ≥
.
•

+ = + + + ≥
.
•
 
+ = + + + ≥ + ≥
.
Cho hai s thc x, y dương thay i . Tìm giá tr nh nht ca biu thc:
( )
= + + +
.
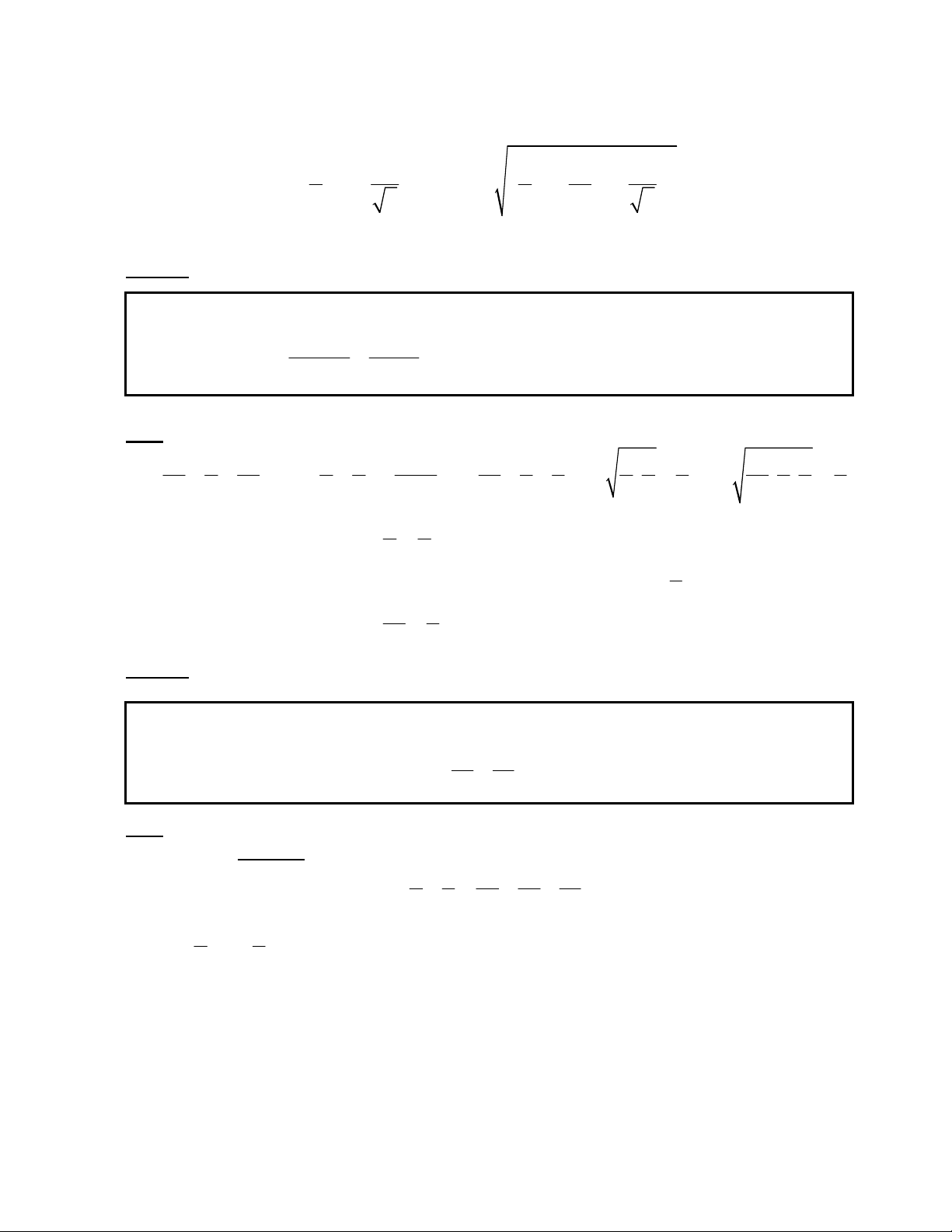
Suy ra
( )
 
= + + + ≥ =
.
Vy giá tr nh nht ca P là 256 khi
= và =.
Ví d 2: ( thi i hc d b khi B nm 2006)
Gii:

+
= + + + = + + + + + ≥ + + =
Du “=” xy ra khi và ch khi
=
+ = ⇔ = =
=
. Vy 
= khi x = y = 2.
Ví d 3: ( thi i hc chính thc khi A nm 2006)
Gii:
Cách 1: (S dng bt ng thc)
Ta có:
( )
 
+ = + − ⇔ + = + − .
t
= = , ta ưc  + = + − .
( )
( )
( )
 = + = + + − = +
( )
⇔ + = + − .
Cho hai s thc x, y dương thay i tha mãn iu kin + ≥ . Tìm giá tr nh nht
ca biu thc
+ +
= + .
Cho hai s thc
≠ và ≠ thay i tha mãn iu kin
( )
 + = + − .
Tìm giá tr ln nht ca biu thc
= + .
vì
 +
≤
nên
( ) ( ) ( )
 +
+
+ = + − ≥ + − =
.
( ) ( )
+ − + ≤ ≤ + ≤ .
Do ó
( )
 = + ≤ .
Vy giá tr ln nht ca A là 16 khi
= = .
Cách 2: (S dng tp giá tr)
Ta có
( )
( )
( )
( )
 


+ − +
++ +
= + = = =
− +
− +
.
Xét biu thc


+ +
=− + . t = thì
+ +
=− + .
• Nu t = 0 thì x = 0 (trái gi thit
≠) nên ≠.
• Do
( ) ( ) ( )
   + = + − ⇔ + = + − nên + = − =
(trái gi thit  ≠). Vy + ≠ nên ≠ − .
Gi T là tp giá tr ca B thì:
∈ ⇔ Phương trình
+ +
=− + có nghim ≠, ≠ − .
⇔ Phương trình
( ) ( )
− − + + − = (*) có nghim ≠, ≠ − .
• Nu m = 1 thì phương trình (*) có nghim t = 0 (loi).
• Nu ≠ thì phương trình (*) có nghim ≠, ≠ −
∆ ≥
⇔ − ≠
≠
.
( ) ( )
+ − − ≥
< ≤
⇔ ≠ ⇔
≠
≠
.
Vì
= và tp giá tr ca B là
(
]
{
}
= nên tp giá tr ca A là
(
]
{
}
 =.
Vy giá tr ln nht ca A là 16.