
KINH NGHI MỆ: H ng d n h c sinh ph ng pháp gi i ướ ẫ ọ ươ ả m t s d ng bài t pộ ố ạ ậ
tính s nhi m s c th l ng b i c a loài ố ễ ắ ể ưỡ ộ ủ trong sinh h c 9.ọ
A. PHẦN MỞ ĐẦU
I. LÝ DO CHỌN ĐỀ TÀI
Nh chúng ta đã bi t, môn sinh h c là b môn khoa h c th c nghi m,ư ế ọ ộ ọ ự ệ
nó có v trí h t s c quan tr ng trong h th ng tri th c khoa h c c a nhân lo i,ị ế ứ ọ ệ ố ứ ọ ủ ạ
có ý nghĩa thi t th c v i đi s ng, kinh t và xã h i loài ng i. Trong hế ự ớ ờ ố ế ộ ườ ệ
th ng ch ng trình sinh h c c p trung h c c s nói chung và sinh h c 9 nóiố ươ ọ ấ ọ ơ ở ọ
riêng, bên c nh nh ng ki n th c thu c v lý thuy t đc mô t còn có m ngạ ữ ế ứ ộ ề ế ượ ả ả
ki n th c không kém ph n quan tr ng đó là ph n bài t p sinh h c. Tuy nhiên,ế ứ ầ ọ ầ ậ ọ
trong ch ng trình sinh h c trung h c c s (THCS) có r t ít ti t bài t p, th iươ ọ ọ ơ ở ấ ế ậ ờ
l ng m i ti t d y trên l p n i dung lý thuy t nhi u nên h u h t giáo viênượ ỗ ế ạ ớ ộ ế ề ầ ế
không th ểcó th i gian h ng d n các em d ng bài t p này đ c ng c ki nờ ướ ẫ ạ ậ ể ủ ố ế
th c lí thuy t cũng nh hình thành kĩ năng làm bài t p.ứ ế ư ậ
Trong chương trình sinh h c 9 thọì d ng bài t p v tính s nhi m s cạ ậ ề ố ễ ắ
th (NST) l ng b i c a loài lể ưỡ ộ ủ à một đề tài hay nh ng cũng khó ưđối với học
sinh. Trong th c ti n gi ng d y môn sinh h cự ễ ả ạ ọ 9 nhi u năm qua,ề tôi nh n th yậ ấ
vi c gi i đc, gi i nhanh, gi i chính xác d ng bài t p này đang còn là v nệ ả ượ ả ả ạ ậ ấ
đ v ng m c và khó khăn không nh ng đi v i các em h c sinh khá gi i màề ướ ắ ữ ố ớ ọ ỏ
ngay c đi v i m t s giáo viên ch a nhi u kinh nghi m. ả ố ớ ộ ố ư ề ệ Qua theo dõi, tôi
th y d ng bài t p này cũng đc g p trong các đ thi h c sinh gi i các c pấ ạ ậ ượ ặ ề ọ ỏ ấ
nh ng s l ng h c sinh đt đi m cao còn ít.ư ố ượ ọ ạ ể
Xu t phát t th c tr ng đó, tôi mu n tìm ra m t gi i pháp giúp h c sinhấ ừ ự ạ ố ộ ả ọ
nh n d ng và gi i nhanh, gi i đúng bài t p sinh h c, trong đó quan tâm đnậ ạ ả ả ậ ọ ế
vi c giúp h c sinh n m v ng m t s d ng bài t p có liên quan đn tính sệ ọ ắ ữ ộ ố ạ ậ ế ố
NST l ng b i c a loài. Chính vì th tôi m nh d n trình bày kinh nghi mưỡ ộ ủ ế ạ ạ ệ
“H ng d n h c sinh ph ng pháp gi i ướ ẫ ọ ươ ả m t s d ng bài t p tính s nhi mộ ố ạ ậ ố ễ
s c th l ng b i c a loàiắ ể ưỡ ộ ủ ” trong công tác b i d ng h c sinh khá gi i mônồ ưỡ ọ ỏ
sinh h c l p 9.ọ ớ
II. ĐỐI TƯỢNG, PHẠM VI NGHIÊN CỨU
1. Đi t ng nghiên c uố ượ ứ
- Áp dụng với đối tượng h c sinh l p 9 (có h c l c t khá tr lên đi v iọ ớ ọ ự ừ ở ố ớ
môn sinh h c).ọ
2. Ph m vi nghiên c uạ ứ
Ph ng pháp gi i m t s bài t p tính s NST l ng b i trong ch ng trìnhươ ả ộ ố ậ ố ưỡ ộ ươ
sinh h c 9: ọ
- Tính theo s tâm đng có trong các t bào con t o ra t t bào m .ố ộ ế ạ ừ ế ẹ
Trang 1

KINH NGHI MỆ: H ng d n h c sinh ph ng pháp gi i ướ ẫ ọ ươ ả m t s d ng bài t pộ ố ạ ậ
tính s nhi m s c th l ng b i c a loài ố ễ ắ ể ưỡ ộ ủ trong sinh h c 9.ọ
- Liên quan đn s l n nguyên phân, s t bào con, s cromatit. ế ố ầ ố ế ố
- Liên quan đn s NST đn đc t o ra và s NST đn c a môi tr ng n iế ố ơ ượ ạ ố ơ ủ ườ ộ
bào cung c p.ấ
- Tính theo s NST ch a hoàn toàn nguyên li u m i.ố ứ ệ ớ
- Tính theo s noãn bào và tinh bào trong gi m phân.ố ả
III. MỤC TIÊU VÀ NHIỆM VỤ NGHIÊN CỨU
- Trao đổi với đồng nghiệp một số d ng bài t p ph n NST trong chạ ậ ầ ương trình
sinh học lớp 9.
- Xây d ng ph ng phápự ươ , h ng d n h c sinh ph ng pháp làm m t sướ ẫ ọ ươ ộ ố
d ng ạbài t p ậtính s NST l ng b i c a loàiố ưỡ ộ ủ .
IV. GIẢ THUYẾT NGHIÊN CỨU
Vi c h ng d n h c sinh ph ng pháp làm m t s d ng ệ ướ ẫ ọ ươ ộ ố ạ bài t p ậtính
s NST l ng b i c a loàiố ưỡ ộ ủ s ẽgiúp h c sinh n m ch c ki n th c lí thuy t vàọ ắ ắ ế ứ ế
có kĩ năng gi i bài t p sinh h c, ả ậ ọ nâng cao kh năng t duy tr u t ng và phânả ư ừ ượ
tích khoa h c cho h c sinh. T o n n t ng đ h c sinh có c h i h c chuyênọ ọ ạ ề ả ể ọ ơ ộ ọ
sâu, t đó cũng t o đc s ham thích h c b môn trong h c sinh.ừ ạ ượ ự ọ ộ ọ
V. PHƯƠNG PHÁP NGHIÊN CỨU
1. Nghiên c u lý thuy tứ ế
Nghiên c u nh ng tài li u liên quan đn đ tài: SGK sinh h c 9, SGV sinhứ ữ ệ ế ề ọ
h c 9, B i d ng h c sinh gi i sinh h c 9, h ng d n gi i bài t p sinh h cọ ồ ưỡ ọ ỏ ọ ướ ẫ ả ậ ọ
9…
2. Th c nghi m s ph mự ệ ư ạ
a) Đi u tra th c tr ng d y và h c ki n th c ch ng “Nhi m s c th ”.ề ự ạ ạ ọ ế ứ ươ ễ ắ ể
* Đi u tra ch t l ng h c t p c a h c sinh ề ấ ượ ọ ậ ủ ọ
- Đi t ng đi u tra: H c sinh khá gi i l p 9 ố ượ ề ọ ỏ ớ
- Hình th c ki m tra vi t: Ra bài t p v nhà, l ng ghép trong bài ki m tra 1ứ ể ế ậ ề ồ ể
ti t.ế
- Ra đê thi hoc sinh gioi tr ng. $ % ươ
- Phi u ki m tra ki n th cế ể ế ứ .
* Đi u tra tình hình gi ng d y c a giáo viên.ề ả ạ ủ
- Trao đi tr c ti p v i các giáo viên d y b môn Sinh h c trong tr ng vàổ ự ế ớ ạ ộ ọ ườ
m t s b n đng nghi p tr ng b n n i dung có liên quan.ộ ố ạ ồ ệ ườ ạ ộ
- D m t s gi d y thao gi ng, d y m u các bài “Nhi m s c th ”; “Nguyênự ộ ố ờ ạ ả ạ ẫ ễ ắ ể
phân”; “Gi m phân”; “Phát sinh giao t ” trong sinh h c 9.ả ử ọ
b) Th c nghi m gi ng d y.ự ệ ả ạ
Trang 2

KINH NGHI MỆ: H ng d n h c sinh ph ng pháp gi i ướ ẫ ọ ươ ả m t s d ng bài t pộ ố ạ ậ
tính s nhi m s c th l ng b i c a loài ố ễ ắ ể ưỡ ộ ủ trong sinh h c 9.ọ
- D y trong các ti t h c ch ng “Nhi m s c th ”.ạ ế ọ ươ ễ ắ ể
- D y trong th i gian b i d ng h c sinh gi i tr ng.ạ ờ ồ ưỡ ọ ỏ ươ
- Ra bài t p v nhà và h ng d n ngoài gi đi v i nh ng h c sinh ham thíchậ ề ướ ẫ ờ ố ớ ữ ọ
h c b môn, h c sinh gi i và nh ng h c sinh có d đnh thi vào tr ngọ ộ ọ ỏ ữ ọ ự ị ườ
chuyên.
VI. ĐÓNG GÓP MỚI VỀ MẶT KHOA HỌC
Trong kinh nghi m này tôi đã h th ng 5 d ng bài t p v tính s NSTệ ệ ố ạ ậ ề ố
l ng b i và h ng d n h c sinh ph ng pháp gi i, s giúp cho h c sinh khiưỡ ộ ướ ẫ ọ ươ ả ẽ ọ
làm bài t p ậd dàngễ xác đnh đc s NST l ng b i c a loàiị ượ ố ưỡ ộ ủ .
Hi v ng kinh nghi m này s là tài li u t t cho h c sinh l p 9 h c b môn, ônọ ệ ẽ ệ ố ọ ớ ọ ộ
thi h c sinh gi i, thi vào các tr ng chuyên môn sinh và h c chuyên sâu. Bọ ỏ ườ ọ ổ
sung vào ngu n tài li u tham kh o d y sinh h c 9 và b i d ng h c sinh gi iồ ệ ả ạ ọ ồ ưỡ ọ ỏ
các c p.ấ
B. PHẦN NỘI DUNG
I. CƠ SỞ KHOA HỌC
1. C s lí lu nơ ở ậ
Ngày nay kh i l ng tri th c khoa h c trên th gi i ngày càng tăng nhố ượ ứ ọ ế ớ ư
vũ bão, nên chúng ta không th hy v ng trong th i gian nh t đnh tr ngể ọ ờ ấ ị ở ườ
ph thông có th cung c p cho h c sinh m t kho tàng trí th c kh ng l màổ ể ấ ọ ộ ứ ổ ồ
loài ng i đã tích lu đc. Vì v y nhi m v c a ng i giáo viên ngày nay,ườ ỹ ượ ậ ệ ụ ủ ườ
không nh ng ph i cung c p cho h c sinh m t v n tri th c c b n mà đi uữ ả ấ ọ ộ ố ứ ơ ả ề
quan tr ng là còn ph i trang b cho h c sinh kh năng t làm vi c, t nghiênọ ả ị ọ ả ự ệ ự
c u đ tìm hi u và t n m b t thêm tri th c. ứ ể ể ự ắ ắ ứ
Trong nh ng năm qua s phát tri n trí tu c a h c sinh ngày càng m nhữ ự ể ệ ủ ọ ạ
m , nhu c u h c t p các môn h c ngày nhi u. Trong đó b môn sinh h cẽ ầ ọ ậ ọ ề ộ ọ
trong nhà tr ng cũng không ng ng b sung, đi sâu và m r ng. Không nh ngườ ừ ổ ở ộ ữ
đc m r ng v lí thuy t mà còn có nhi u d ng bài t p nh m ki m tra khượ ở ộ ề ế ề ạ ậ ằ ể ả
năng v n d ng các ki n th c lý thuy t c a h c sinh. ậ ụ ế ứ ế ủ ọ
2. C s th c ti nơ ở ự ễ
Bài t p Sinh h c là m t lĩnh v c d gây h ng thú, tìm tòi đi v i h cậ ọ ộ ự ễ ứ ố ớ ọ
sinh. Thông qua quá trình gi i bài t p h c sinh có th hi u và c ng c ki nả ậ ọ ể ể ủ ố ế
th c lí thuy t r t t t mà không gây s nhàm chán hay lãng quên. M t trong cácứ ế ấ ố ự ộ
d ng bài t p đó là bài t p v tính s NST l ng b i c a loài, nó k t n i gi aạ ậ ậ ề ố ưỡ ộ ủ ế ố ữ
lí thuy t v i th c ti n. Thông qua d ng bài t p này h c sinh có đc nh ngế ớ ự ễ ạ ậ ọ ượ ữ
Trang 3

KINH NGHI MỆ: H ng d n h c sinh ph ng pháp gi i ướ ẫ ọ ươ ả m t s d ng bài t pộ ố ạ ậ
tính s nhi m s c th l ng b i c a loài ố ễ ắ ể ưỡ ộ ủ trong sinh h c 9.ọ
hi u bi t nh t đnh v NST liên quan đn ki n th c di truy n ng i, t đóể ế ấ ị ề ế ế ứ ề ườ ừ
các em tự trang b cho mình nh ng ki n th c c n thi t đ gi i các bài t p, đị ữ ế ứ ầ ế ể ả ậ ề
thi có liên quan hay áp d ng trong cu c s ng, bi t gi i thích các tr ng h pụ ộ ố ế ả ườ ợ
khác bi t trong t nhiên (có liên quan đn NST).ệ ự ế
Trong th i gian đc t chuyên môn phân công gi ng d y môn sinh h cờ ượ ổ ả ạ ọ
9 (khi ch a áp d ng chuyên đ) và 1 s l n đc phòng GDĐT phân côngư ụ ề ố ầ ượ
ch m thi h c sinh gi i,ấ ọ ỏ tôi nh n th y ậ ấ ph n l n ầ ớ h c sinh n m ch a v ng n iọ ắ ư ữ ộ
dung ki n th c và các d ng bài t p ế ứ ạ ậ liên quan đn tính s NST l ng b i c aế ố ưỡ ộ ủ
loài trong ph m vi ch ng trình sinh h c l p 9ạ ươ ọ ớ . Đng th i trong ti t d y trênồ ờ ế ạ
l p, do yêu c u c a bài h c nên giáo viên cũng không có đ th i gian đớ ầ ủ ọ ủ ờ ể
h ng d n h c sinh ph ng pháp gi i bài t p này. Vì v y đ ướ ẫ ọ ươ ả ậ ậ ể làm đc, làmượ
đúng, làm nhanh bài t p v “tính s NST l ng b i c a loài” thì h c sinhậ ề ố ưỡ ộ ủ ọ
c n ph i n m v ng môt sô dang và ph ng pháp gi i.ầ ả ắ ữ $ $ ươ ả
II. ĐÁNH GIÁ THỰC TRẠNG
T th c tr ng đã nêu trên, tr c khi áp d ng kinh nghi m này tôi đã ừ ự ạ ướ ụ ệ
ti n hành kh o sát ch t l ng h c sinh b ng phi u kh o sát (ế ả ấ ượ ọ ằ ế ả phi u s 1ế ố ) sau:
1. Phi u kh o sát ế ả
(Th i gian làm bài 120 phút)ờ
Bài 1. (1,0 đi m)ể Có 1 t bào nguyên phân m t s l n liên ti p t o ra 16 tế ộ ố ầ ế ạ ế
bào con có ch a tât ca 128 tâm đông. Xác đnh b nhi m NST c a loài? ư % $ ị ộ ễ ủ
Bài 2 . (2,0 đi m)ể Nuôi c y trong ng nghi m 20 t bào xôma c a 1 loài quaấ ố ệ ế ủ
m t s l n nguyên phân liên ti p b ng nhau thu đc 1280 t bào.ộ ố ầ ế ằ ượ ế
N u trong các t bào thu đc nói trên khi các NST đu tr ng thái t nhânế ế ượ ề ở ạ ự
đôi thì đm đc t t c 20480 crômatit. Tính b NST l ng b i c a loài?ế ượ ấ ả ộ ưỡ ộ ủ
Bài 3 . (2,0 đi m)ể Ba h p t ti n hành nguyên phân:ợ ử ế
- H p t A nguyên phân 4 l n liên ti p nh n c a môi tr ng 360 NST. ợ ử ầ ế ậ ủ ườ
- H p t B t o ra s t bào con b ng 1/2 s t bào con c a h p t A. Trongợ ử ạ ố ế ằ ố ế ủ ợ ử
các t bào con có 192 NST.ế
- H p t C nguyên phân 5 l n t o ra các t bào con có t t c 768 tâm đng.ợ ử ầ ạ ế ấ ả ộ
Xác đnh b NST c a m i h p t và nêu k t lu n?ị ộ ủ ỗ ợ ử ế ậ
Bài 4 . (2,5 đi m)ể L y 50 t bào xôma cho nguyên phân liên ti p thì nh n th yấ ế ế ậ ấ
nguyên li u c n cung c p tệ ầ ấ ư ng đơ ư ng 16800 NST đn. Trong s NST c aơ ơ ố ủ
các t bào con thu đc ch có 14400 NST là đc c u thành hoàn toàn tế ượ ỉ ượ ấ ừ
nguyên li u m i c a môi tr ng n i bào. Tính b NST lệ ớ ủ ườ ộ ộ ư ng b i c a t bào?ỡ ộ ủ ế
Trang 4
KINH NGHI MỆ: H ng d n h c sinh ph ng pháp gi i ướ ẫ ọ ươ ả m t s d ng bài t pộ ố ạ ậ
tính s nhi m s c th l ng b i c a loài ố ễ ắ ể ưỡ ộ ủ trong sinh h c 9.ọ
Bài 5. (2,5 đi m)ể T bào sinh d c s khai 1 loài nguyên phân nhi u đt t o raế ụ ơ ề ợ ạ
t bào sinh d c NST lế ụ ư ng b i 2n. Trong quá trình nguyên phân môi tr ngỡ ộ ườ
n i bào cung c p 690 NST. Các t bào sinh d c tham gia t o tinh trùng nhộ ấ ế ụ ạ ưng
ch có 3,125% s tinh trùng sinh ra tham gia th tinh v i tr ng t o 2 h p t .ỉ ố ụ ớ ứ ạ ợ ử
Xác đnh b NST 2n c a loài?ị ộ ủ
(Đáp án chi ti t có trong ph n gi i pháp)ế ầ ả
2. K t qu kh o sátế ả ả
Kh o sát v i 30 h c sinh (20 em l p 9A và 10 em còn l i c a kh i 9). K t ả ớ ọ ớ ạ ủ ố ế
qu s h c sinh đt đi m cao còn r t ít. C th nh sau:ả ố ọ ạ ể ấ ụ ể ư
Sô hoc sinh tham gia kiêm tra$ % 30 em
Sô đat điêm 8, 9, 10$ % 0 em (0%)
Sô điêm 6,7%8 em (26,67 %)
Sô điêm d i 6% ướ 22 em (73,33 %)
Sô điêm 1, 2%7 em (23,33 %)
III. CÁC GIẢI PHÁP
1. Ph n lý thuy tầ ế
T k t qu kh o sát trên và trong quá trình gi ng d y, tôi nh n th yừ ế ả ả ả ạ ậ ấ
nguyên nhân ch y u là do h c sinh ch a có đc h th ng ki n th c và kủ ế ọ ư ượ ệ ố ế ứ ỹ
năng, ph ng pháp c n thi t đ đnh h ng cách gi i bài t p d ng này. Vìươ ầ ế ể ị ướ ả ậ ạ
v y, mu n v n d ng ki n th c m t cách linh ho t, tr c h t yêu c u h cậ ố ậ ụ ế ứ ộ ạ ướ ế ầ ọ
sinh ph i n m v ng đc ki n th c c b n và công th c áp d ngả ắ ữ ượ ế ứ ơ ả ứ ụ . Các ki nế
th c c b n liên quan c n n m v ng là: ứ ơ ả ầ ắ ữ
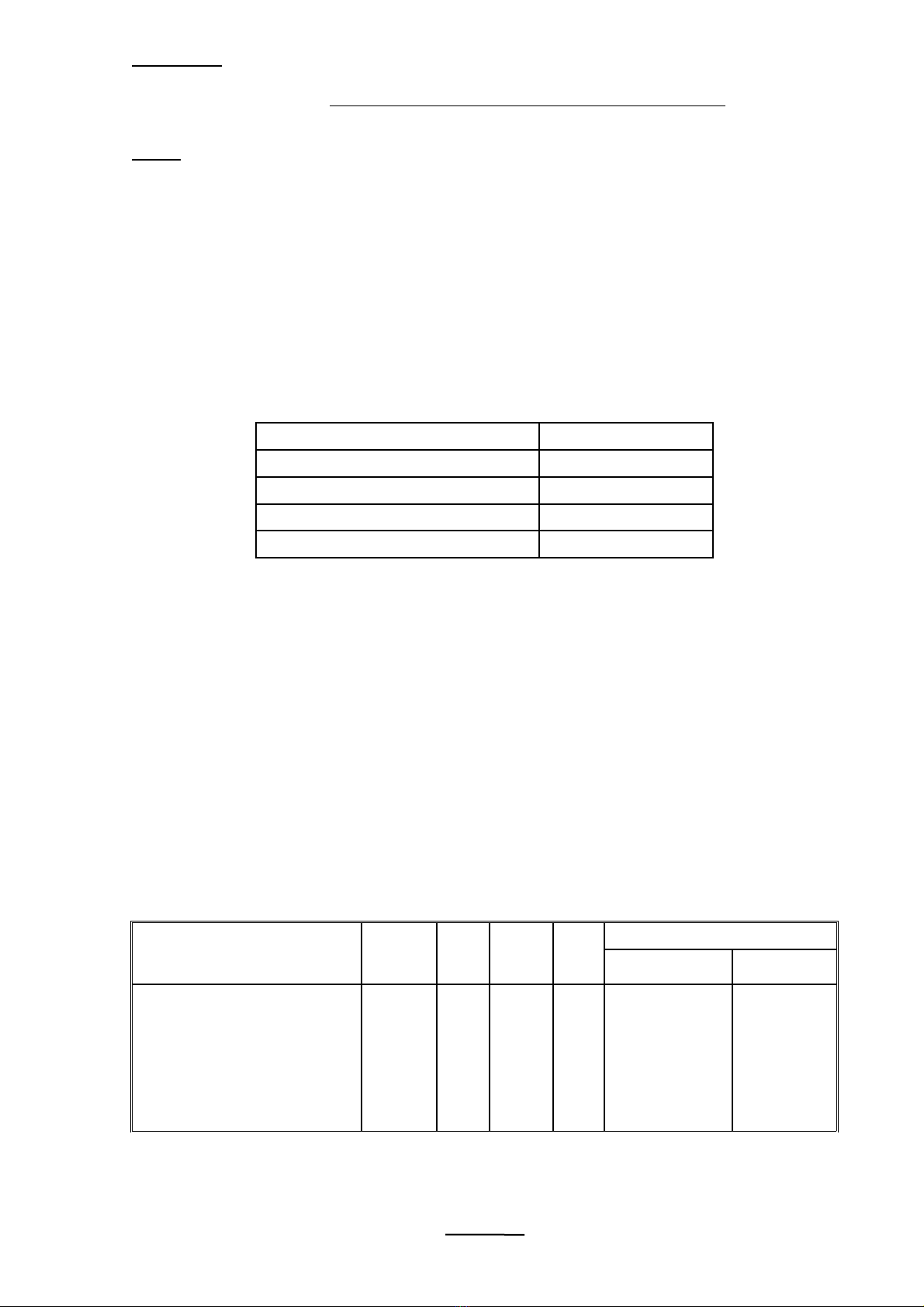
Kiên th c vê nguyên phân ư
* S NST, s crômatit và s tâm đng trong m i t bào (TB) t ng kì c a ố ố ố ộ ỗ ế ở ừ ủ
quá trình nguyên phân.
Kì
C u trúcấ
Trung
gian
Đầ
u
Gi aữSau Cu iố
TB ch a táchưTB đã tách
S NST ố
Tr ng thái NSTạ
S crômatitố
S tâm đng (= s ố ộ ố
NST)
2n
kép
4n
2n
2n
kép
4n
2n
2n
kép
4n
2n
4n
đnơ
0
4n
4n
đnơ
0
4n
2n
đnơ
0
2n
Trang 5


























