
CEAC – Học thuật Xây dựng Bách Khoa 1
TÀI LIỆU HƯỚNG DẪN MÔN HỌC CƠ HỌC KẾT CẤU
CEAC – Học thuật Xây dựng Bách Khoa 2
Định nghĩa:
Tính chất:
❖Trong hệ luôn tồn tại thành phần lực nằm ngang ngay cả khi tải trọng chỉ tác
dụng theo phương thẳng đứng.
❖Nội lực trong hệ ba khớp nhỏ hơn trong hệ đơn giản cùng nhịp, cùng chịu tải
trọng.
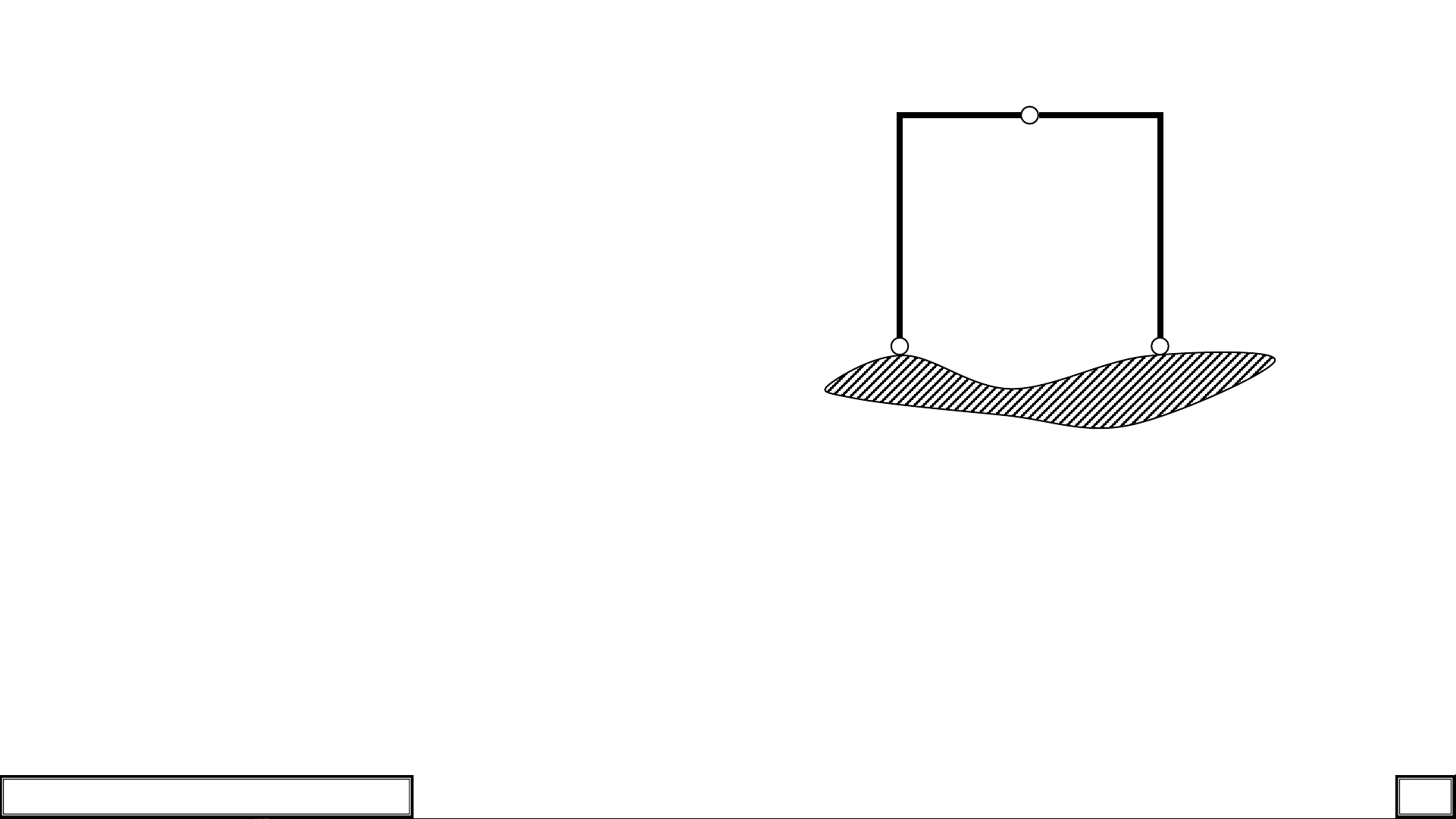
Hệ ba khớp là hệ gồm hai miếng
cứng nối với nhau bằng một khớp
và liên kết với Trái Đất bằng hai
khớp (gối cố định)để tạo thành hệ
bất biến hình.
Hình 1.1. Hệ ba khớp
CEAC – Học thuật Xây dựng Bách Khoa 3
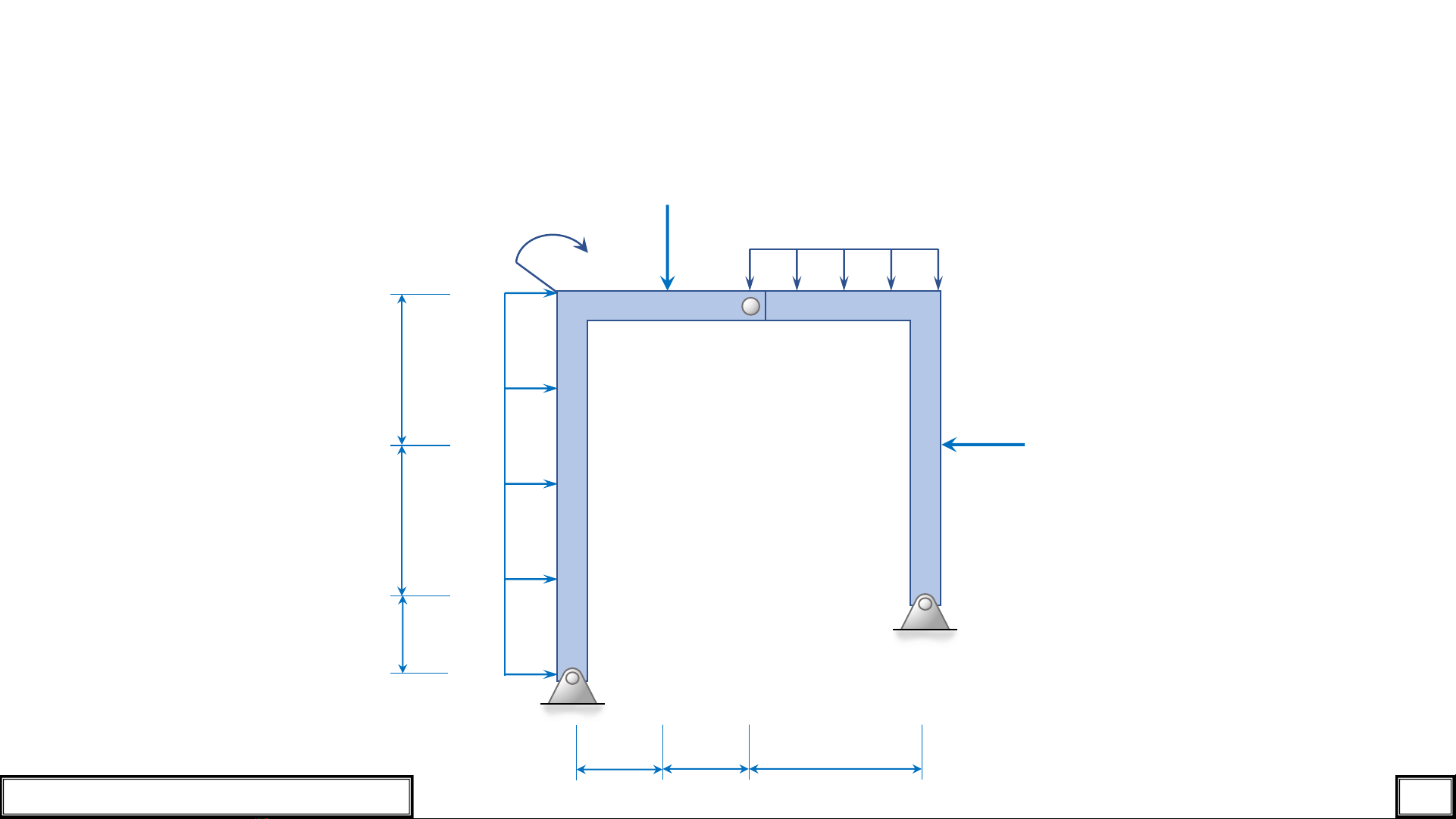
Vấn đề 1:
Cho hệ kết cấu chịu tác dụng của các tải trọng như hình vẽ (bỏ qua trọng lượng bản
thân kết cấu).Vẽ biểu đồ nội lực của hệ kết cấu trên.
Hình 1.1
q
2qL
qL2
C
A
L
L/2L/2
L
L
L/2
B
q
qL
CEAC – Học thuật Xây dựng Bách Khoa 4
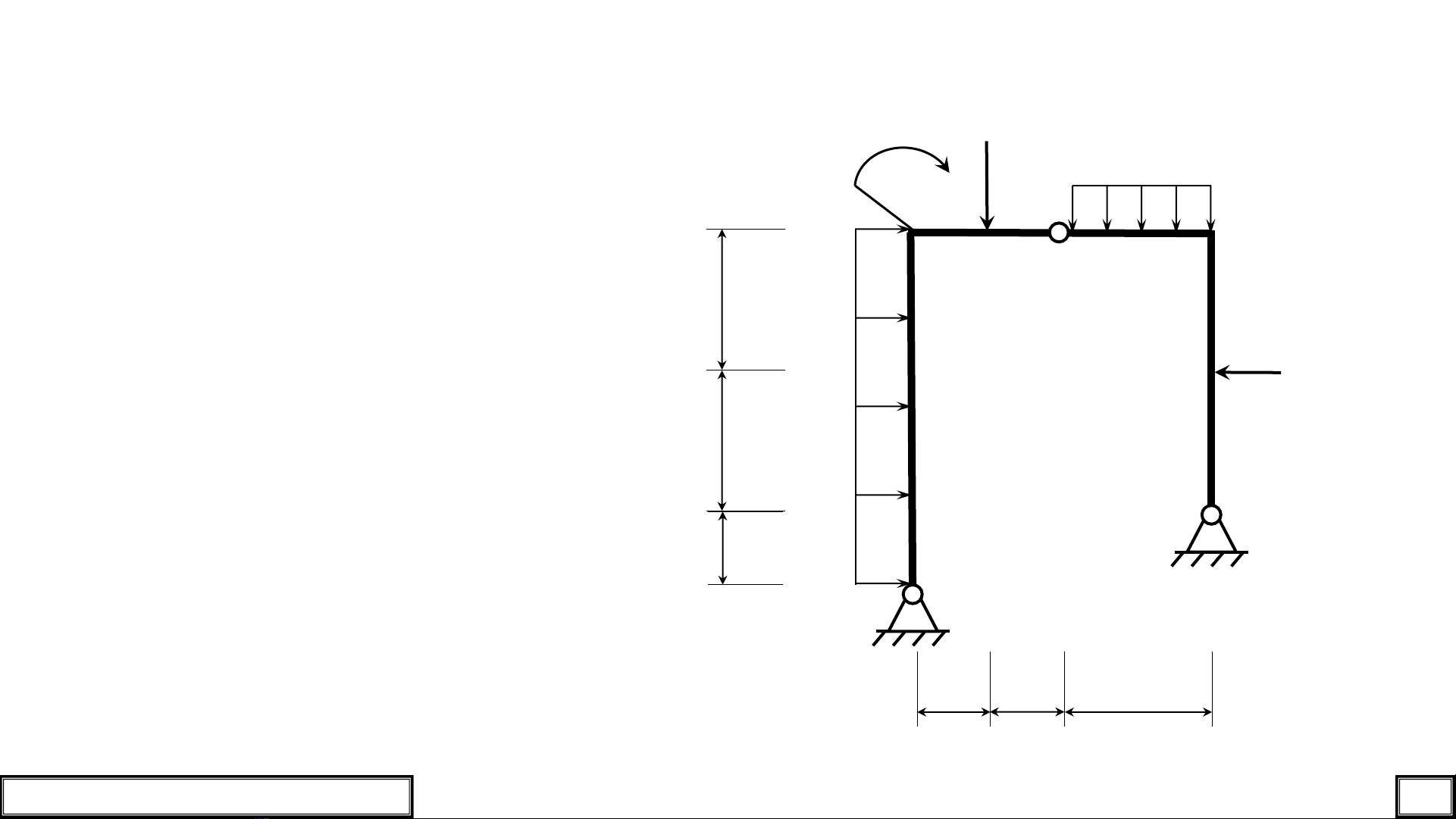
Đáp án tham khảo:
Bước 1:
Lập sơ đồ tính.
Hình 1.2
✓Xác định đúng điểm đặt,
phương chiều, độ lớn của lực và
momen;
✓Phân tích sơ đồ tính có phải là
hệ ba khớp hay không dựa trên
định nghĩa.
→Hệ trong ví dụ này là hệ gồm 3
khớp thật ở các vị trí A, B, C.
L
L
A
B
C
2qL q
qL2
q
qL
L/2 L
L/2
L/2
CEAC – Học thuật Xây dựng Bách Khoa 5
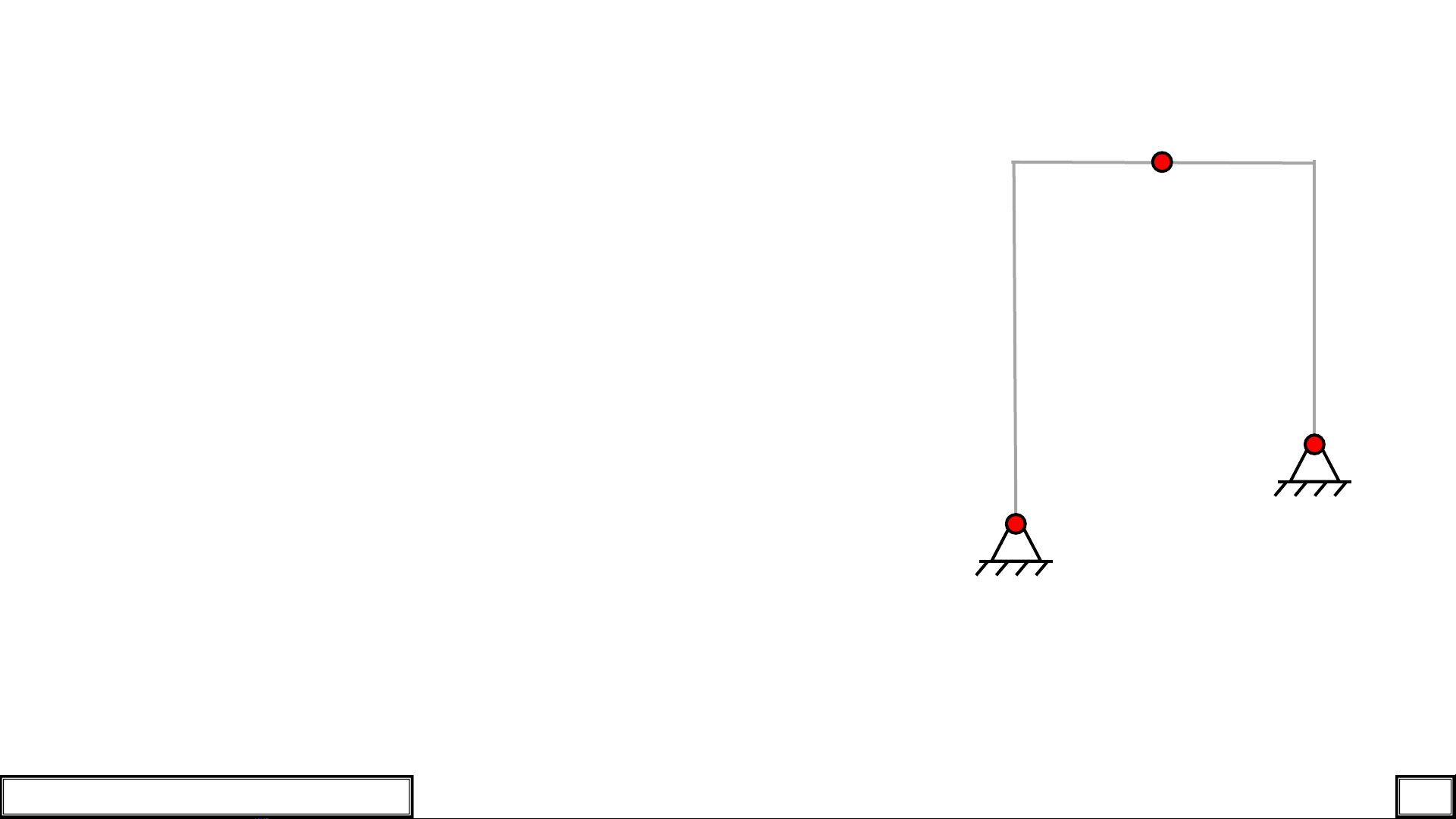
Bước 2:
Giải phóng liên kết.
✓Giải phóng liên kết ở các gối tựa;
✓Áp dụng cân bằng momen cho các gối tựa.
✓Sau đó, giải phóng liên kết ở khớp nối hai phần
của hệ;
✓Chú ý rằng, chiều của lực ở khớp nối hai hệ
phải ngược nhau ( định luật III Newton);
✓Ở mỗi nửa hệ, cân bằng momen cho khớp nối.A
B
C
Hình 1.3


























