Giaùo aùn Hình hoïc 10NC – Chöông 3
Tieát 40 - 41 §6. ÑÖÔØNG HYPEBOL
I. MUÏC TIEÂU: Giuùp hoïc sinh:
1. Veà kieán thöùc :
•Nhôù ñöôïc ñònh nghóa ñöôøng hypebol vaø caùc yeáu toá xaùc ñònh ñöôøng ñoù
nhö: tieâu cöï, tieâu ñieåm, taâm sai, ...
2. Veà kyõ naêng:
•Vieát ñöôïc pt chính taéc cuûa hypebol khi bieát caùc yeáu toá xaùc ñònh hypebol.
•Töø pt chính taùc cuûa hypebol, thaáy ñöôïc tính chaát vaø chæ ra ñöôïc caùc tieâu
ñieåm, ñænh, hai ñöôøng tieäm caän cuûa hypebol.
3. Veà tö duy:
• Bieát aùp duïng vaøo baøi taäp.
4. Veà thaùi ñoä:
•Reøn luyeän tính nghieâm tuùc khoa hoïc.
•Xaây döïng baøi moät caùch töï nhieân chuû ñoäng.
II. CHUAÅN BÒ PHÖÔNG TIEÄN DAÏY HOÏC:
•Hoïc sinh xem baøi tröôùc ôû nhaø.
•Chuaån bò caùc baûng nhoû ghi ñeà baøi vaø duøng ñeå hoïc sinh traû lôøi theo
nhoùm.
III. GÔÏI YÙ VEÀ PHÖÔNG PHAÙP DAÏY HOÏC:
•Phöông phaùp môû vaán ñaùp thoâng qua caùc hoaït ñoäng ñieàu khieån tö duy.
IV. TIEÁN TRÌNH BAØI HOÏC VAØ CAÙC HOAÏT ÑOÄNG :
1. Kieåm tra baøi cuõ vaø daïy baøi môùi:
Hoaït ñoäng cuûa GV vaø HS Noäi dung cô baûn
GV vaøo baøi baèng ñthò cuûa haøm soá y= 1/x
hay chæ cho hs thaáy vuøng saùng haét leân
böùc töôøng töø moät ñeøn baøn (hình 86 sgk)
GV ghi ñ/n ñöông hypebol
Coù theå hdaãn hs caùch veõ hypebol nhö hình
88 sgk, cho hs veà nhaø thöû laøm.
Hoaït ñoäng 1: Gi i bài toán tìm ph ng trìnhả ươ
chính t c c a hypebol:ắ ủ
Tr c h t ta tính bk qua tiêu c a m i đi m Mướ ế ủ ỗ ể
thu c hypebol.ộ
GV hdaãn hs choïn heä truïc tñoä Oxy (h 89 sgk)
? Em haõy cho bieát toaï ñoä cuûa 2 tieâu ñieåm
F1 vaø F2.
GV: gsöû
( ) ( )
;M x y H∈
. Haõy tính bieåu
1. Ñònh nghóa ñöôøn g hypeb ol:
Ñònh nghóa: sgk
2. Pt chính taéc cuûa hypeb ol:
Ta coù:
M(x;y)
F2
F1O x
y
( )
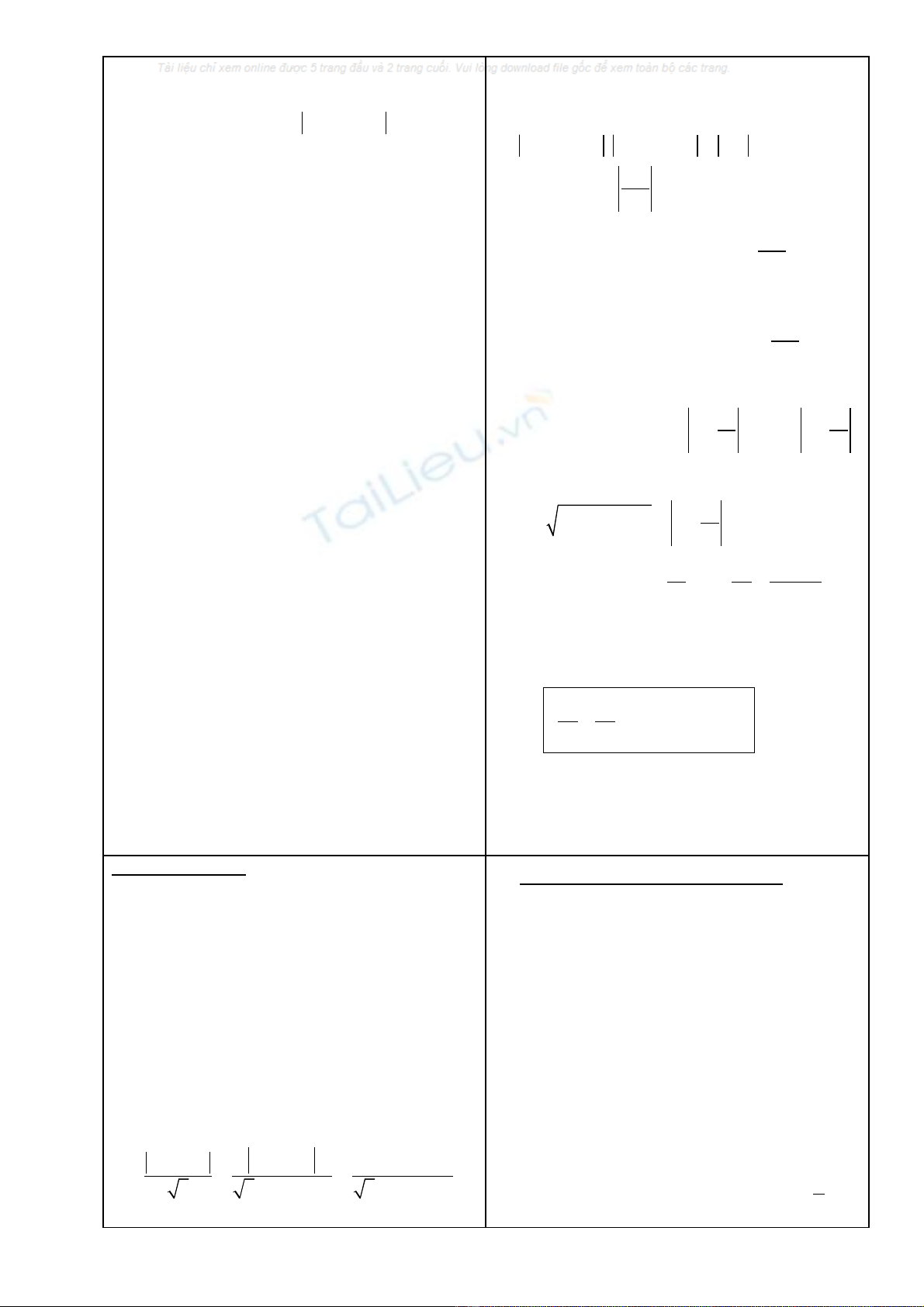
2 2
2 2
1 0, 0
x y a b
a b
− = > >
Giaùo aùn Hình hoïc 10NC – Chöông 3
thöùc
2 2
1 2
MF MF−
.
GV: haõy sduïng gthieát
1 2
2MF MF a− =
ñeå tính MF1, MF2 = ?
GV: baây giôø ta seõ laäp pt cuûa (H)
ñoái vôùi heä toaï ñoä ñaõ choïn.
M(x;y), F1(-c; 0) => MF1 = ?
Keát hôïp vôùi keát quaû vöøa tìm
ñöôïc ta coù:
Bình phöông 2 veá vaø ruùt goïn
ñthöùc ta ñöôïc ?
Nx:
2 2
? 0a c−
( ) ( )
2 2
2 2 2 2
1 2
2 2
1 2
1 2 1 2
1 2
,
4
. 4
2
MF x c y MF x c y
MF MF cx
MF MF MF MF cx
cx
MF MF a
= + + = − +
⇒ − =
⇒ − + =
⇒ + =
Khi x > 0 ta coù
1 2
1 2
2
2 ,
cx
MF MF a
MF MF a
+ =
− =
Khi x < 0 ta coù
Töø ñoù suy ra
1 2
,
cx cx
MF a MF a
a a
= + = −
Ta coù:
( )
( )
22
1
22 2
22
2 2 2
1
cx
MF x c y a a
cx x y
x c y a a a a c
= + + = +
⇔ + + = + ⇔ + =
÷ −
Vì
2 2
0a c− <
neân ñaët
2 2 2
a c b− = −
hay
2 2 2
, 0b c a b= − >
, ta ñc:
(1)
Ngöôïc laïi, coù theå CM ñc raèng: neáu
M(x;y) thoaû (1) thì M thuoäc (H).
Pt (1) ñgl pt chính ta é c cuûa hypebol
Hoaït ñoäng 2:
GV: töø ptct (1) cuûa (H), haõy neâu
nhöõng tính chaát cuûa hypebol naøy?
GV nhaéc laïi ?3 trong §5 (phaàn elip)
ñeå hs coù theå laøm töông töï.
Hình veõ 90 sgk
Yeâu caàu hs laøm hñ3 trang 107 sgk
ñeå hs coù theå hieåu yù nghóa cuûa
( )
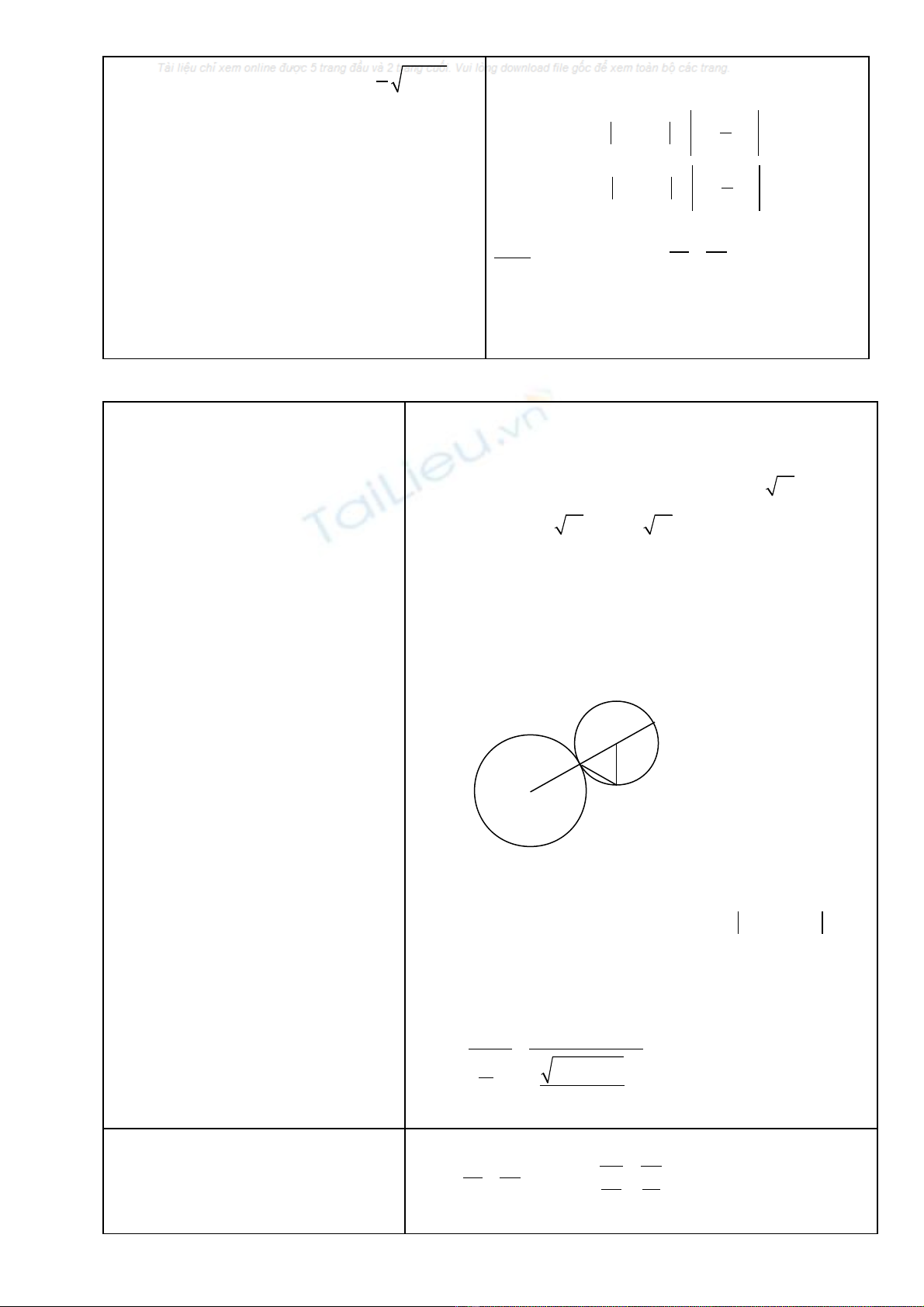
2 2
: 4 4H x y− =
, tcaän: x – 2y = 0
K/c töø M0(x0 ; y0) ñeán ñöôøng tcaän
( ) ( )
2 2
0 0
0 0
0 0 0 0
4
24
5 5 2 5 2
x y
x y
dx y x y
−
−
= = =
+ +
3. Hình daïng cuûa hype b ol:
•O laø taâm ñx; Ox, Oy laø 2 truïc
ñx cuûa(H).
•Truïc thöïc naèm treân Ox, ñoä
•Truïc aûo naèm treân Oy, ñoä
•2 ñænh: (-a;0) vaø (a;0)
•2 tieâu ñieåm F1(-c;0), F2(c;0)
•Taâm sai e = c/a (e >1)
•Pt caùc caïnh cuûa hcn cô sôû
,x a y b= ± = ±
•Pt 2 ñöôøng tieäm caän
b
y x
a
= ±
Giaùo aùn
Khi x0 > 0 taêng leân thì
2
0 0
14
2
y x= −
cuõng taêng leân, do ñoù k/c d caøng
giaûm daàn.
Cho hs lên b ng làm ví d .ả ụ
Cho h c sinh gi i ví d theo nhóm và nh n xétọ ả ụ ậ
cho đi m .ể
•Bk qua tieâu cuûa
( )
M H∈
:
1
2
M M
M M
c
MF a ex a x
a
c
MF a ex a x
a
= + = +
= − = −
VD: Cho hypebol (H):
2 2
1
16 9
x y
− =
Xñònh toaï ñoä caùc ñænh, caùc tieâu
ñieåm vaø tính tam sai, ñoä daøi truïc
thöïc, ñoä daøi truïc aûo cuûa (H).
Hoaït ñoäng 3: söûa bt
HS traû lôøi mieäng baøi 36. GV
nhaän xeùt vaø chænh söûa.
* Goïi 3 HS leân baûng söûa 3 baøi
taäp töông öùng:
Hs1: Neâu ptct cuûa (H), hình daïng
cuûa noù vaø laøm bt 37a.
Hs2: laøm bt 37c.
Hs3: laøm bt 38.
* Hoïc sinh trong 4 toå thaûo luaän
veà lôøi giaûi cuûa caùc baïn vaø ñöa
ra nhaän xeùt cuûa toå mình.
* Gv nhaän xeùt vaø söûa chöõa caùc
sai soùt neáu coù .
36. Caùc mñ a), b), d) ñuùng, mñ c) sai.
37.
a) (H) coù a = 3, b = 2,
2 2 2
13 13c a b c= + = ⇒ =
Tieâu ñieåm:
( ) ( )
1 2
13;0 , 13;0F F−
Ñoä daøi truïc thöïc: 2a = 6
Ñoä daøi truïc aûo: 2b = 4
Pt caùc ñöôøng tcaän: y = ± 2/3x
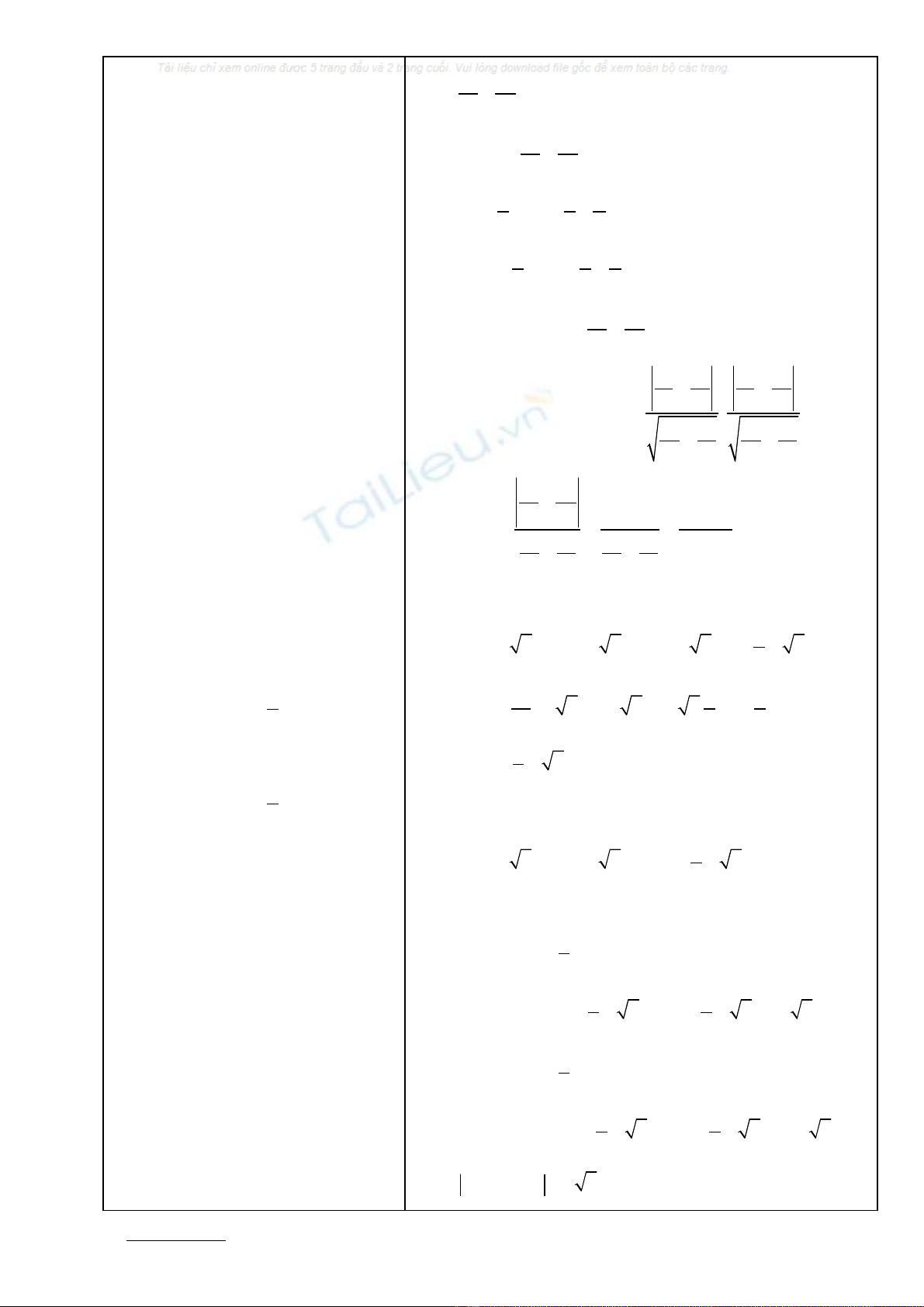
38. Goïi M laø taâm (C’) ñi qua F
2, tx vôùi (C).
Ta coù: 2 ñtroøn tx ngoaøi
1 2
MF R MF⇔ = +
2 ñtroøn tx trong
1 2
MF MF R⇔ = −
Vaäy (C) tx (C’)
1 2 1 2
MF MF R MF MF R⇔ − = ± ⇔ − =
Do ñoù taäp hôïp caùc taâm M cuûa (C’) laø 1 (H)
coù 2 tieâu ñieåm laø F1, F2; ñoä daøi truïc thöïc
baèng R/2. Ptct cuûa (H) ñoù laø:
2 2
2 2
2
1 2
1
22
x y
RF F R
− =
−
÷ ÷
÷
* Goïi 3 HS leân baûng söûa 3
baøi taäp töông öùng:
Hs1: laøm bt 39a,b.
39. a)
2 2
1
16 9
x y
− =
b)
2 2
1
27 12
13 13
x y
− =
(C’)
(C)
F1F2
M
Giaùo aùn
Hs2: laøm bt 39c.
Hs3: laøm bt 40.
* Hoïc sinh trong 4 toå thaûo
luaän veà lôøi giaûi cuûa caùc
baïn vaø ñöa ra nhaän xeùt
* Gv nhaän xeùt vaø söûa
chöõa caùc sai soùt neáu coù .
GV hd hs laøm bt 41.
Tính
2 2
1 2
,MF MF
theo cthöùc ñaõ
bieát
(chuù yù ptích theo haèng
ñaúng thöùc)
Xeùt 2 TH:
+ Neáu x > 0 thì
1?xx
+ ≥
1 2
?MF MF− =
+ Neáu x < 0 thì
1?xx
+ ≤
1 2
?MF MF− =
töø ñoù suy ra ñpcm.
c)
2 2
1
1 4
x y
− =
40. Xeùt (H):
2 2
2 2
1
x y
a b
− =
. Hai ñöôøng tcaän cuûa
1
:b
y x
a
∆ =
hay
0
x y
a b
− =
2
:b
y x
a
∆ = −
hay
0
x y
a b
+ =
( ) ( )
2 2
0 0
0 0 2 2
; 1
x y
M x y H a b
∈ ⇔ − =
Ta coù:
( ) ( )
0 0 0 0
1 2
2 2 2 2
; . ; .
1 1 1 1
x y x y
a b a b
d M d M
a b a b
− +
∆ ∆ =
+ +
2 2
0 0
2 2
2 2
2 2 2 2
1
1 1 1 1
x y
a b a b
a b
a b a b
−
= = = +
+ +
khoâng
41.
( ) ( ) ( )
2
2 2 2
2
1
1
2 2 2 2MF x y x x
= + + + = + + +
÷
( )
2
2
2
2
1 1 1
2 2 2 2 2 2
12
x x x
x x x
xx
= + + + + +
= + +
÷
Töông töï
( ) ( )
2
2 2
2
2
1
2 2 2MF x y x x
= − + − = + −
÷
Töø ñoù suy ra:
Neáu x > 0 thì
12xx
+ ≥
1 2
1 1
2 2 2 2MF MF x x
x x
− = + + − + − =
÷ ÷
Neáu x < 0 thì
12xx
+ ≤ −
1 2
1 1
2 2 2 2MF MF x x
x x
− = − + + + + − = −
÷ ÷
Vaäy
1 2
2 2MF MF− =
2. Cuûng coá : Nhaéc laïi caùc noäi dung chính cuûa baøi
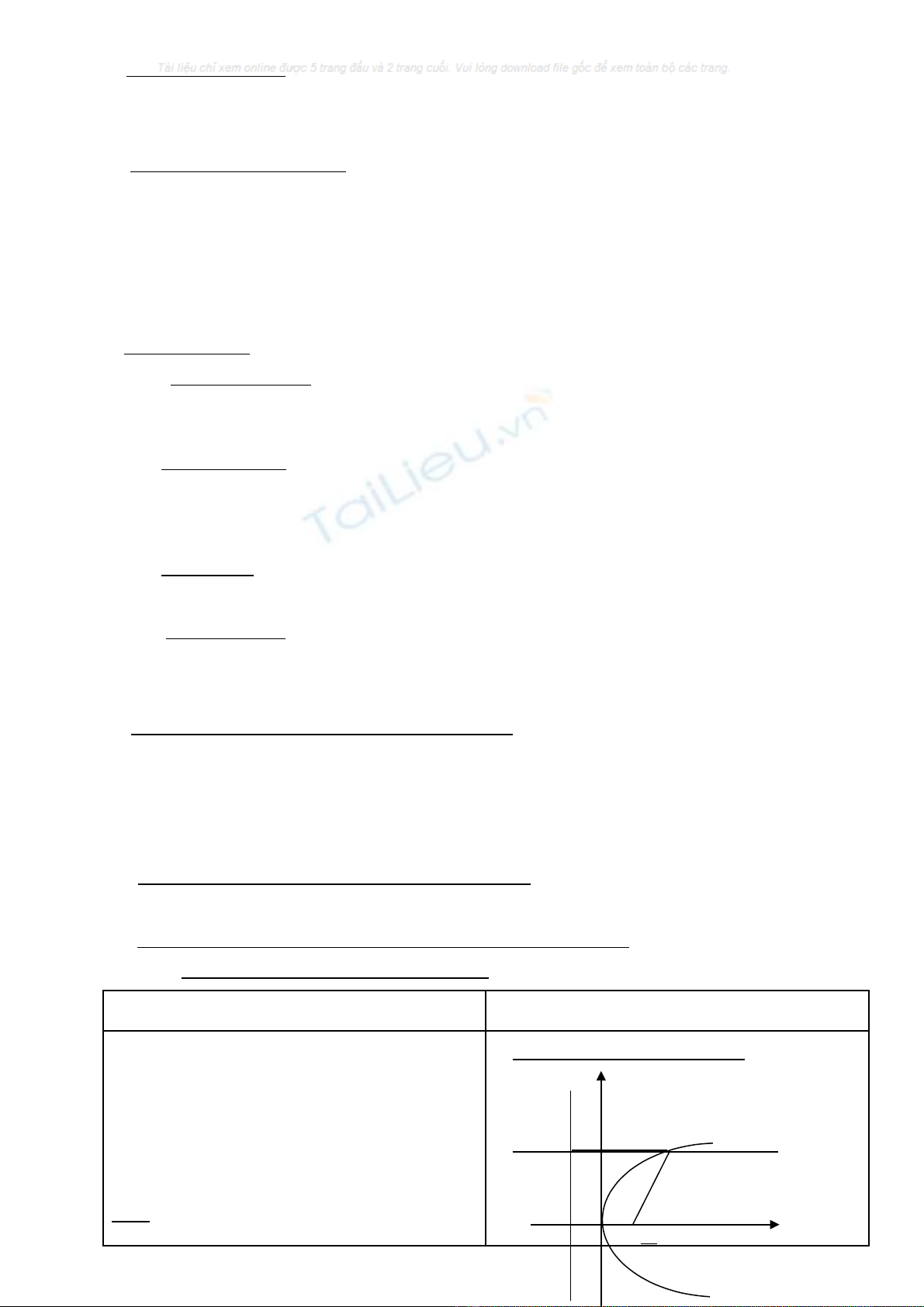
M(x;y)
P
;0
2
p
F
÷
x
y
O
∆
Giaùo aùn Hình hoïc 10NC – Chöông 3
3. Baøi taäp veà nhaø:
oLaøm theâm bt trong sbt
oÑoïc vaø soaïn tröôùc baøi “Ñöôøng parabol”.
V. RUÙT KINH NGHIEÄM:
Tieát 42 - 43 §7. ÑÖÔØNG PARABOL
I. MUÏC TIEÂU: Giuùp hoïc sinh:
1. Veà kieán thöùc :
•Nhôù ñöôïc ñònh nghóa ñöôøng hypebol vaø caùc khaùi nieäm: tieâu ñieåm, ñöôøng
chuaån, tham soá tieâu cuûa parabol.
2. Veà kyõ naêng:
•Vieát ñöôïc pt chính taéc cuûa parabol khi bieát caùc yeáu toá xaùc ñònh parabol vaø
xñònh ñöôïc tieâu ñieåm, ñöôøng chuaån cuûa parabol khi bieát pt chính taéc cuûa
parabol.
3. Veà tö duy:
• Bieát aùp duïng vaøo baøi taäp.
4. Veà thaùi ñoä:
•Reøn luyeän tính nghieâm tuùc khoa hoïc.
•Xaây döïng baøi moät caùch töï nhieân chuû ñoäng.
II. CHUAÅN BÒ PHÖÔNG TIEÄN DAÏY HOÏC:
•Hoïc sinh xem baøi tröôùc ôû nhaø.
•Hoïc sinh ñaõ ñöôïc hoïc ñthò cuûa hs baäc 2.
•Chuaån bò caùc baûng nhoû ghi ñeà baøi vaø duøng ñeå hoïc sinh traû lôøi theo
nhoùm.
III. GÔÏI YÙ VEÀ PHÖÔNG PHAÙP DAÏY HOÏC:
•Phöông phaùp môû vaán ñaùp thoâng qua caùc hoaït ñoäng ñieàu khieån tö duy.
IV. TIEÁN TRÌNH BAØI HOÏC VAØ CAÙC HOAÏT ÑOÄNG :
1. Kieåm tra baøi cuõ vaø daïy baøi môùi:
Hoaït ñoäng cuûa GV vaø HS Noäi dung cô baûn
GV vaøo baøi baèng ñthò cuûa haøm soá baäc 2
vaø 1 soá vd thöïc teá veà parabol.
GV ghi ñ/n ñöôøng parabol
Coù theå hdaãn hs caùch veõ parabol nhö hình
93 sgk, cho hs veà nhaø thöû laøm.
Hñ1: Gi i bài toán tìm ph ng trình chính t cả ươ ắ
c a parabol:ủ
1. Ñònh nghóa ñöôøng parabol: (sgk)
2. Phöông trình ctaéc cuûa parabol: